Physique, concours
admission en formation des ingénieurs de l'ENSM 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Question
1.
On
considère que la planète Neptune et son satellite Triton peuvent être
considérés comme des solides ponctuels car les rayons ou les
demi-grands-axes des orbites sont supposés grands devant les dimensions
de Neptune ou de ses satellites.
Neptune : masse : MN = 1,025 x 1026 kg
Triton : masse : M1 =2,147 x 1022 kg
rayon orbital : R1 =NT= 3,547 x 105 km
période de révolution : Trev = 5,877 jours solaires
vitesse orbitale : v0 = 4 km.s-1.
Constante de gravitation : G = 6,67 x 10–11 m3.kg-1.s-2 ; 1 jour solaire = 86 400 s.
Le mouvement de Triton.
L’orbite de Triton est circulaire. On appelle N le centre d’inertie de Neptune, T le centre d’inertie de
Triton et u le vecteur unitaire de direction (NT).
1. Donner l’expression vectorielle de la force gravitationnelle F exercée par Neptune sur son
satellite Triton et calculer sa valeur numérique.
2. Montrer que le mouvement de Triton est uniforme en utilisant l’expression de l’accélération dans
la base locale de Frenet .
3. Etablir l’expression littérale de la valeur de sa vitesse V sur son orbite en fonction des grandeurs
MN, R1=NT et G.
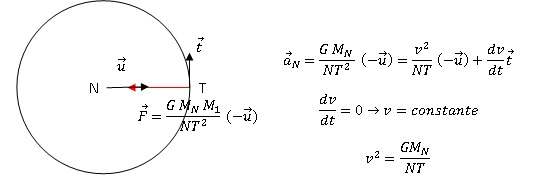
F = 6,67 10 -11 * 1,025 x 1026 *2,147 x 1022 /( 3,547 x 108)2=1,167 1021 N.
4. Calculer cette vitesse V et la comparer à celle donnée dans l’énoncé.
v = [ 6,67 10-11 *1,025 x 1026 /( 3,547 x 108)]½=4,39 103 m/s = 4,39 km/s.
Valeur supérieure de 10 % par rapport à celle de l'énoncé.
5. Montrer que la période de révolution Trev de Triton peut s’exprimer en fonction de MN, R1 et G.
Triton décrit la circonférence 2pR1 à la vitesse v en une durée Trev.
2pR1 = v Trev.
Elever au carré : 4p2R12 = v2 T2rev=GMN /R1T2rev.
T2rev = 4p2R13 /(GMN) ; Trev=2pR1 [R1 /(GMN)]½.
6. Calculer la valeur de Trev et la comparer à la valeur donnée par l’énoncé.
Trev=2*3,14*3,547 x 108[3,547 x 108 /(6,67 10-11 *1,025 x 1026 )]½.
Trev=5,076 105 s ou 5,076 105 /86400 = 5,875 jours solaires.
|
|
|
Question 2.
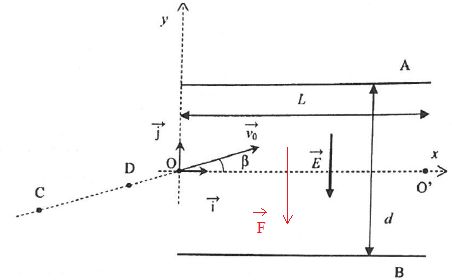
Un proton pénètre en O entre deux plaques (A) et (B) d’un condensateur plan où règne un champ
électrique uniforme E. Le vecteur vitesse v0 fait un angle b avec l’axe Ox.
Le mouvement du proton est étudié dans le référentiel terrestre supposé galiléen.
Données : g = 9,81 m.s-2 ; e = 1,60.10-19 C ; mproton = m=1,67.10-27 kg ; E = 5000 V.m-1 ;
L = 20,0 cm ; d = 10,0 cm ; b = 10° ; v0 = 1,0.106 m.s-1.
1. Montrer que le poids du proton est négligeable devant la force électrique qui s’exerce sur lui.
P = mproton g = 1,67 10-27 *9,81 =1,64 10-26 N.
F = e E = 1,60 10-19 * 5000 =8,00 10-16 N, valeur très supérieure au poids.
2. Déterminer le signe et la valeur de la tension UAB qui existe entre les deux plaques.
Le champ électrique pointe vers le plus petit potentiel, celui de B ; UAB >0.
3. Etablir les caractéristiques du vecteur accélération du proton.
4. Etablir les équations horaires x(t) et y(t) du mouvement du proton.
5. Etablir l’équation cartésienne y = f(x) de la trajectoire du proton. Indiquer la nature de la trajectoire.
6. Déterminer les coordonnées xS et yS du point de sortie S du proton de l’espace compris entre les deux plaques.
La trajectoire est une branche de parabole.
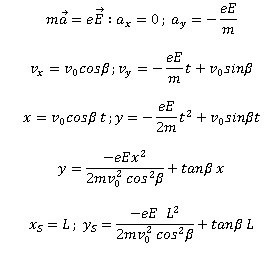
A.N : ay= -1,6 10-19 *5000 / (1,67 10-27) = -4,79 1011 m s-2.
vx = 1,0 106 cos 10 = 9,85 105 m s-1 ;
vy = 1,0 106 sin 10 - 4,79 1011 t = 1,74 105 -4,79 1011 t.
x =9,85 105 t ; y = -2,4 1011 t2 + 1,74 105.
y = -0,247 x2 +0,176x.
xS = 0,200 m ; yS =-0,247 *0,202 +0,176 *0,2 =2,53 10-2 m
|
|
|
|
Question 3.
On a réalisé l’enregistrement du son émis par une guitare et celui du diapason qui a servi à l’accorder.
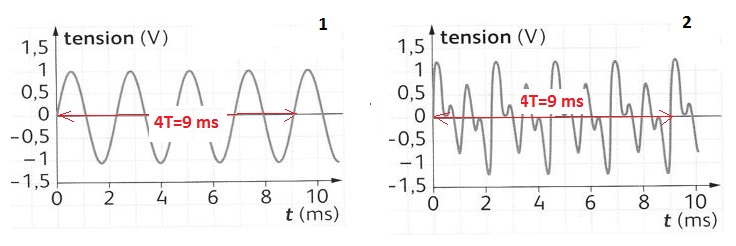
1. Attribuer à chaque instrument son enregistrement en justifiant votre réponse.
Le son émis par le diapason est pur : la tension est sinusoïdale ( 1).
Le son émis par la guitare est complexe (2).
2. Calculer la fréquence de chacun des sons. Conclure.
T = 910-3 / 4 =2,25 10-3 s ; f= 1/(2,25 10-3) = 444 Hz.
Les deux sons ont la même hauteur.
3. Indiquer l’allure possible du spectre en fréquence de chacun des instruments.
Le spectre du diapason possède un seul pic à 444 Hz ; celui de la
guitare possède en plus des harmoniques siuées à des fréquences
multiples de celle du fondameental.
Le niveau sonore du son émis par la guitare est L = 70 dB pour un spectateur situé à 5 m de distance.
Il est calculé à l’aide de la relation L = 10 log(I / I0) = 10 log (I / (1,0 10-12))
dans laquelle I set l’intensité sonore du son.
4. Calculer la valeur de l’intensité sonore I du son émis par la guitare.
I = I0 100,1L =1,0 10-12 * 107 = 1,0 10-5 W m-2.
5. Déterminer le
niveau sonore du son perçu par le même spectateur si deux guitares
identiques placées à la même distance jouaient en même temps.
L' = 10 log (2 I / (1,0 10-12)) =L +10log2 = 73 dB.
6. Calculer quel
devrait-être le nombre de guitares identiques placées à la même
distance pour que le niveau sonore atteigne 79 dB.
Itotal = 1,0 10-12 * 107,9 = 7,94 10-5 ~ 8 10-5 W m-2.
Huit guitares identiques placées à la même distance du spectateur.
|
Question 4.
La laine de verre sert à isoler d’un point de vue thermique. Elle existe en différentes épaisseurs : e1 = 100 mm et e2 = 200 mm par exemple.
Pour un échantillon de surface S1 = 2,00 m2 de laine de verre d’épaisseur e1 le flux thermique est F = 10 W pour une différence de température entre les deux faces est DT1 = 20 °C.
Pour un échantillon de surface S2 = 1,78 m2 de laine de verre d’épaisseur e2 l’énergie transférée est Q2 = 40 kJ pour une durée Dt2 = 2,0 heures lorsque la différence de température entre les deux faces est DT2 = 25 °C.
1. Déterminer la valeur et l’unité de la résistance thermique Rth1 de la laine de verre d’épaisseur e1.
F = DT1 / RTh1 ; RTh1 = DT1 / F =20 /10=2 K W-1.
2. Déterminer la valeur et l’unité de la résistance thermique Rth2 de la laine de verre d’épaisseur e2.
Flux thermique : Q2 / Dt2 = 40 103 / (2*3600) =5,55 W.
RTh1 =25 / 5,55= 4,5 K W-1.
La conductivité thermique d’un matériau est donnée par la relation : l = e / (S Rth).
3. Calculer les conductivités thermiques l1 et l2 des deux laines de verre en justifiant leur unité.
l1 =0,100 / (2,00 *2)=0,025 m m-2 K-1W soit 0,025 W K-1 m-1.
l2 =0,200 / (1,78 *4,5)= 0,025 W K-1 m-1.
4. Comparer l1 et l2 et conclure.
Les deux valeurs sont identiques : la conductivité thermique caractérise un matériau.
5. Déterminer l’expression de F en fonction de e, S et DT.
F = DT / RTh =DT l S / e.
6. Indiquer la stratégie à adopter pour limiter les pertes d’énergie.
Le flux thermique doit être le plus faible posible : la conductivité
thermique du matériau doit être faible et son épaisseur importante.
|
|