Mathématiques,
concours
officier chef de quart marine 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice 1.
1. Développer (2x+1)(x-1).
2x2-2x+x-1 = 2x2-x-1.
2. Résoudre dans R les équations suivantes.
a. 2(lnx)2 -lnx -1 = 0.
On pose X = ln x ; 2X2-X-1 = 0.
D'après la question précédente : (2X+1)(X-1)=0
X = -½, soit ln x = -0,5 ; x ~0,61 ;
X = 1 soit x = e ~2,72.
b. 2e-2x -e-x-1 = 0.
On pose X = e-x ; 2X2-X-1 = 0.
D'après la question précédente : (2X+1)(X-1)=0.
X = -½, soit e-x = -0,5 , impossible e-x est toujours positif.
X = 1 soit e-x=1 x = 0.
Exercice 2.
Soit X une variable aléatoire de loi uniforme sur l’intervalle [-5 ; 5].
1. Donner la fonction densité de probabilité de X.
a = -5 et b = 5.
f(x) = 1 / (b-a) = 1 / (5-(-5)) = 1 / 10 = 0,1 si x appartient à [-5 ; +5] sinon zéro.
2. Calculer l’espérance et la variance de X.
E(x) = (a+b) / 2 = (-5 +5) / 2 = 0.
V(x) = (a-b)2 /12 =(-5 +5)2 / 12 = 0.
3. Quelle est la probabilité que X appartienne à l’intervalle [2 ; 4] ?
p(a <= X <= ß) = (ß-a) / (b-a) =(4-2) / 10 = 0,2.
4. Sachant que X est supérieur à 1, quelle est la probabilité que X appartienne à [2 ; 4] ?
p((X>1) = p( 2<= X <5) =(5-2) / 10 =0,3.
p((X>1) ∩p(2 <= X <= 4)= p(2 <= X <= 4)=0,2.
[ p((X>1) ∩p(2 <= X <= 4) ] / p((X>1) =0,2 / 0,3 = 2 / 3.
Exercice 3. Le plan complexe est muni d’un repère orthonormé direct (O, u, v) d’unité graphique 1 cm.
On considère le nombre complexe suivant :
z = (1-2i) / 5½.
On appelle M, A, B et C les points d’affixes respectives z , conjugué de z , -1 / z et -i / (2z).
1. Ecrire ces complexes sous forme algébrique.
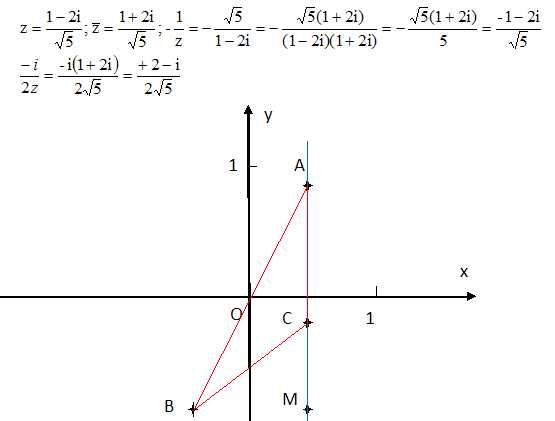
2. Montrer que les points A, C et M appartiennent à une même droite. Donner l’équation cartésienne de cette droite.
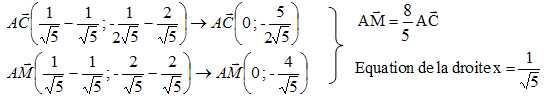
3. Déterminer AC et BC. En déduire que le triangle ABC est isocèle en C.
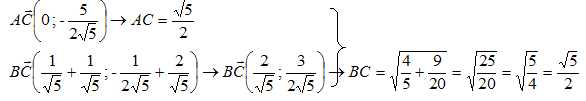
AC = BC, le triangle ABC est isocèle en C.
4. Ecrire le nombre complexe suivant sous forme exponentielle et en déduire la nature du triangle ABM.
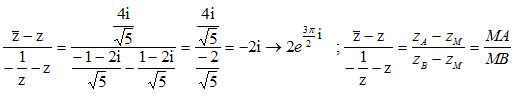
MA et MB sont perpendiculaires ; le triangle ABM est rectangle en M.
|
|
|
Exercice 4.
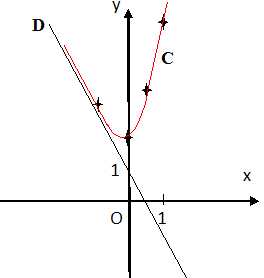
Soit la fonction définie par f(x) =1-2x+e2x.
. On appelle C la courbe représentative de la fonction f dans un plan rapporté à un repère orthonormé d’unité graphique 1 cm.
1. Déterminer la limite de f en -oo.
Le terme en exponentielle tend vers zéro ; f(x) tend vers +oo.
2. Montrer que la droite D d’équation y = 1-2x est asymptote à la courbe C en -oo.
f(x) -y =1-2x+e2x-1+2x = e2x.
f(x) -y tend vers zéro lorsque x tend vers -oo la droite d'équation y = 1-2x est asymptote à la courbe C en -oo.
f(x) -y étant positive, la courbe C est au dessus de l'asymptote.
Donner la position de C par rapport à cette asymptote.
3. Montrer que pour tout xnon nul, on a f(x) = x [1 /x -2 +e2x / x].
En déduire la limite de f en +oo.
Dans l'expression de f(x), mettre x en facteur commun :
f(x) = f(x) = x [1 /x -2 +e2x / x].
Quand x tend vers +oo :
1 /x tend vers zéro ; e2x / xtend vers l'infini.
f(x) tend vers l'infini quand x tend vers +oo.
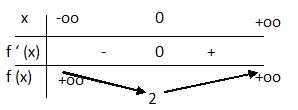
4. Calculer la dérivée de f et donner le tableau de variation de f.
f '(x) = -2+2e2x= 2(e2x-1)
f '(x) =0 si x = 0.
5. Tracer D et C.
|
|
|
|
Exercice 5.
On considère pour n positif ou nul, un une suite géométrique de premier terme u0 et de raison q différente de zéro, vérifiant :
u3 x u4 x u5 = 27 et u32 + 2u3 +u42 = 8.
1. Exprimer u3 x u4 x u5 en fonction de u4.
u1 = q u0 ; u2 = q2 u0 ; u3 = q3 u0 ; u4 = q4 u0 ; u5 = q5 u0 ;
u3 = u4 / q ; u5 = q u4 ; u3 x u4 x u5 = u43.
2. Déterminer les termes u4 puis u3.
. En déduire que q = -3 et calculer le terme u0.
u43 = 27 soit u4 = 3.
u32 + 2u3 +u42 = 8 ; u32 + 2u3 +9 = 8 ; u32 + 2u3 +1 = 0 ;
(u3+1)2 = 0 soit u3 = -1.
q = u4 / u3 = 3 / (-1) = -3.
u2 = u3 / q = -1/(-3) = 1 /3 ; u1 = u2 / q = - 1 /9 ; u0 = u1 / q = 1 / 27.
3. On pose vn = u2n+3 pour tout n positif ou nul.
. Montrer que la suite vn est une suite géométrique. Donner son premier terme et sa raison.
u n+1 =q un =qn+1 u0 ; u n+2 =qn+2 u0 ; u n+3 =qn+3 u0 ; u n+4 =qn+4 u0 ;
v0 =q6 u20 ; v1 =u24 = q8 u20 ; v2 =u25 = q10 u20 = q2 v1.
vn = u2n+3 = q2n+6 u20 ;
vn+1=u2n+4 = q2n+8 u20 = q2 vn.
Vn est une suite géométrique de premier terme q6 u20 =(-3)6 x (1 / 27)2 =1 et de raison q2 = 9.
|
|