Radioactivité,
mécanique, diffraction, sphère chargée, électronique,
concours EMIA 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Désintégration du césium en baryum.
Un atome de Césium 137 13755Cs
se désintègre e baryum 13756Ba en émettant
une particule ß-.
1.
Ecrire l'équation de cette réaction nucléaire. Quelles lois sont
utilisées ?
13755Cs ---> 0-1e
+13756Ba.
Conservation de la charge : 55 = -1 +56 ; conservation du nombre de
nucléons : 137 = 0 +137.
2. Donner la signification de 13755Cs et définir
la notion d' isotope.
Le noyau de césium compte 55 protons et 137-55 = 82 neutrons.
Des isotopes ne diffèrent que par leur nombre de neutrons. Ils ont le
même numéro atomique.
3. Une source radioactive contient 1018
noyaux de césium 137 à la date t0. On mesure son activité à
la date t1 : A1 = 5,7 108 Bq. On donne
la période radioactive du césium 137 : t½ = 30,17 ans.
3.1. Qu'appelle
-ton
période radioactive ?
La période rzdioactive est la durée au bout de laquelle la moitié des
noyaux initiaux se sont désintégrés.
3.2. Calculer la valeur de la
constante radioactive du césium 137. Calculer la date t1.
l t½
= ln(2) ; l =
ln(2) / 30,17=0,02297 an-1 ou
0,02297 /(365 x 24 x3600) =7,285 10-10 s-1.
A0 = l
N0 = 7,285 10-10
x1018= 7,285
108 Bq.
A= A0exp(-l t) ; ln(A0/A) =
lt ; t
= ln((7,285 108/
(5,7 108)) / 0,02297 =10,7 ans..
Mécanique du point.
Tir vertical d'une balle avec un FAMAS.
Calibre : D = 5,56 mm ; masse de la balle
m = 4 g ; vitesse initiale de la balle : v0 = 900 m/s
; Coefficient de taînée de cette balle CD=0,3 ; g =
9,81 m s-2.
Partie I : tir vertical dans le vide.
1.
Faire un schéma de la balle en vol et représenter l'(es) effort(s)
appliqué(s) à cette balle assimilée à un point matériel.
Dans le vide , la balle n'est soumise qu'à son poids.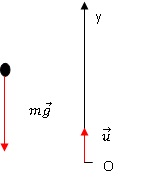
1.2.
La balle quitte l'arme et gagne de l'altitude.
1.2.1.
Enoncer la seconde loi
de Newton.
Dans
un référentiel galiléen, la somme vectorielle des forces extérieures
appliquées au système est égale à la masse du système multipliée par le
vecteur accélération de son centre d'inertie.
1.2.2. Appliquer cette loi et
déterminer au bout de combien de temps la balle atteint l'altitude
maximale
.Accélération a = -g ; vitesse v = - gt +v0 ; position y =
-½gt2+v0t.
A l'altitude maximale, la vitesse est nulle : t = v0 / g =
900 / 9,81 =91,7 s. Ce résultat paraît peu cohérent
1.3. La balle
redescend vers le sol..
Quelle vitesse la balle atteint-elle au niveau du sol ?
La conservation de l'énergie mécanique implique que la vitesse finale
est égale à la vitesse initiale .
Partie
II. Prise en compte de la résistance de l'air.
Cette force est modélisée par F = 0,5 rSCDv2.
r =1,25
kg m-3, masse volumique de l'air ; S : surface
transversale maximale du projectile ; CD coefficient de
traînée ; v : vitesse de la balle.
La balle est étudiée dans sa phase de chute vers le sol.
2.1 et 2.2 Faire un
schéma de la situation. Etablir l'équation différentielle régissant le
mouvement.
La poussée d'Archimède due à l'air peut être négligée devant le poids.
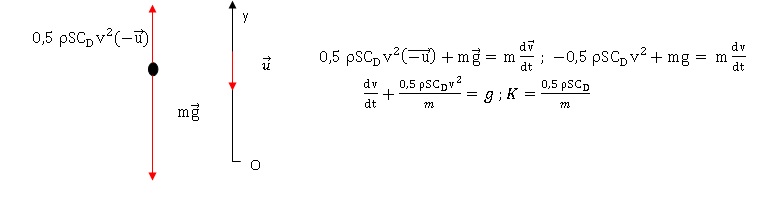
2.3. Déduire de
cette équation différentielle l'expression d'une vitesse limite.
La vitesse augmente au début de la chute. La force de frottement croît
avec le carré de la vitesse. Lorsque cette force est opposée au poids,
la vitesse devient constante.
dVlim/dt =0 ; 0,5 rSCD
V2lim = mg ; V2lim
=2mg /(rSCD) ; Vlim
= [2mg /(rSCD)]½.
2.4. La balle
atteint au sol 99% de sa vitesse limite. Un impact sur le corps humain
avec une énergie de 15 J peut induire des dommages corporels
importants, conclure sur la dangerosité de ce tir.
S = 3,14 x(5,56 10-3)2 / 4 = 2,43 10-5
m2.
Vlim
=[2 x 0,004 x9,81 / (1,25 x2,43 10-5 x0,3)]½
=92,8 m /s.
Energie cinétique de la balle : ½m(0,99 x Vlim)2
= 0,002 x91,872=16,9 J, valeur supérieure à15 J.
Il peut y avoir des dommages corporels.
|
|
|
Physique des ondes.
On intercale devant un faisceau laser une plaque avec une fente
rectangulaire de largeur a = 0,04 mm. On place après cette plaque un
écran. La distance fente-écran est D = 3 m. On a représenté la figure
obtenue sur l'écran. La largeur L de la tache centrale mesure 8,2 cm.
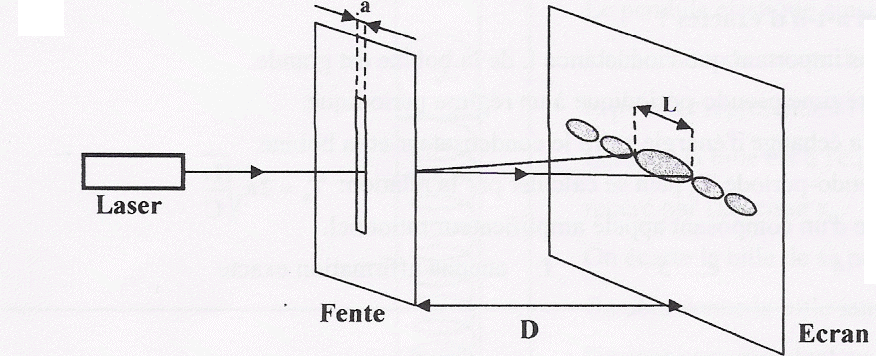
1.
Comment se nomme le phénomène observé ?
Diffraction des ondes par une fente..
2 On rappelle que
l'écart angulaire entre le milieu de la tache centrale et la première
extinction vérifie la relation q
= l / a. Calculer
la longueur d'onde du laser.
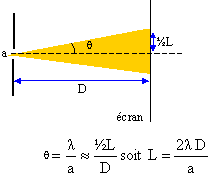
l = aL / (2D) = 4 10-5 x0,082 /
6=5,47 10-7 m = 547 nm.
3. La houle est un mouvement
ondulatoire de la surface de la mer formée par un vent lointain. Un
vent de 80 km/h engendre une houle dont les vagues font 1,5 m de
hauteur. Ces vagues sont espacées de 225 m. Elles s'enchainent toutes
les 10 s.
3.1. Calculer la
vitesse de déplacement des vagues à la surface de l'eau..
l =
225 m ; T = 10 s ; v = l
/T = 225 / 10 = 22,5 m/s.
3.2. Cette
houle arrive au niveau d'un port dont la largeur D = 1000 m et dont
l'entrée a une largeur a = 200 m. Un bateau est amarré au fond du port
à une distance de 400 m de l'entrée. Le bateau ressentira t-il les
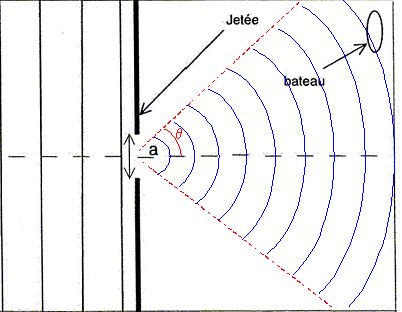
effets de la houle ? Pourquoi ? Faire un schéma explicatif.
Cette houle
arrive sur un port dont l'ouverture entre deux jetées a une
largeur a = 200 m, valeur du même ordre de grandeur que la longueur
d'onde des vagues : on s'attend donc à un phénomène de diffraction avec
q=l/a=
225/200 = 1,125 radian ou 64°.
Le bateau ressent donc les effets de la houle.
3.3. Donner
la définition d'une onde mécanique. La lumière est-elle une onde
mécanique ? La houle est-elle une onde longitudinale ou transversale ?
Justifier.
Une onde mécanique est la propagation
d'une perturbation dans un milieu matériel, avec transport d'énergie,
sans transport de matière.
La houle est une onde mécanique transversale : la direction de la
déformation est perpendiculaire à la direction de propagation.
La lumière est une onde électromagnétique.
|
|
|
|
Cinématique
du point. Hockey sur glace.
Un joueur
glisse sur une patinoire avec le palet guidé par sa crosse. Le patineur
se déplace à la vitesse VP par rapport à la patinoire telle
que ses composantes sont : VPx = -2 et VPy
=-6 . Il frappe le palet en lui donnant une vitesse v = 25 m/s
par rapport à lui, dans la direction du centre du but O. Au moment de
la frappe, le palet est en R de coordonnées xR = 4 ; yR
= 4.
1.
Rappeler les
caractéristiques d'un vecteur.
Un vecteur est défini par son point d'application, sa direction, son
sens et sa norme.
2. Donner les
caractéristiques du vecteur
vitesse du palet par rapport au joueur qui le frappe. Exprimer ensuite
les composantes de cette vitesse dans le repère.
3. Déterminer la
vitesse du palet par rapport au repère fixe.
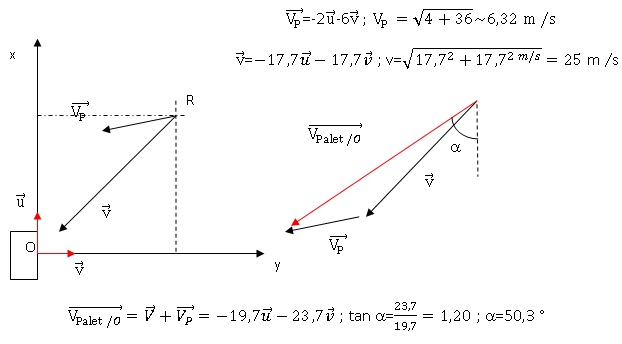
4. La largeur du but est de1,83 m
et le gardien n'est pas assez rapide pour bloquer le palet. Le but
est-il marqué ?
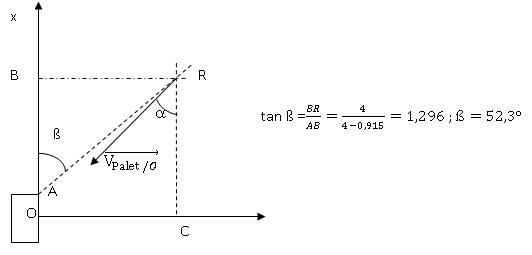
ß > a : le but
est marqué.
|
|
Champ électrostatique
d'une sphère chargée en surface.
O centre de la sphère de rayon R ; Q >0, charge surfacique de la
sphère.
1. Exprimer le
vecteur champ électrostatique en un point M situé à la distance r du
centre de la sphère.
Soit un point M situé à l'intérieur de la
sphère, à une distance OM=x du centre.
Par raison de symétrie le champ est radial.
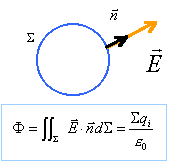
On considère une sphère S
, de centre O et de rayon x.
D'après le théorème de Gauss, le flux du vecteur champ
électrique à travers la surface S
est nul car il n'y a pas de charge à l'intérieur de S.
si x < R, le champ électrique est nul à l'intérieur
de la sphère.
Soit un point M situé à une distance x > R
F = E 4px²
D'autre part la charge contenue à l'intérieure de S est la charge totale de la sphère de
rayon R : Q = s 4pR².
d'où E = s R² / (e0x²)
On retrouve la discontinuité de la composante normale du
champ (s / e0) à la traversée d'une surface chargée.
2.
En déduire le potentiel électrostatique V(M).
( le potentiel
électrique est nul à l'infini).
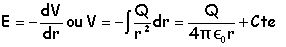
La constante
d'intégration est nulle, le potentiel électrique étant nul à l'infini.
A l'extérieur de la sphère : V = Q/(4p
e0 r).
A la surface de la sphère : V = Q/(4p
e0 R).
Il y a continuité du potentiel à la traversée de la surface de la
sphère.
Potentiel constant à l'intérieur de la sphère V0 = Q/(4p e0 R).
Mécanique.
On remplit un verre
d'eau contenant des glaçons à ras bord. Que se passe t-il lorsque les
gmaçons vont fondre ?
Trois propositions sont faites.
1. La glace occupe un plus grand volume que le liquide, le niveau de
l'eau va donc baisser dans le verre.
2. Comme pour les glaces aux pôles qui vont faire monter l'eau des mers
avec le rechauffement climatique, l'eau va déborder du verre.
3. Le niveau de l'eau ne va pas changer dans le verre.
Quelle est la bonne explication ? Justifier.
1 est fausse, car une partie de la glace est immergée ( 90 %) et
une autre partie émerge ( 10 %).
2 est fausse, le niveau des mers montera à cause de la fonte des
glaces continentales et de la dilatation de l'eau.
3. est vraie.
Générateur de Thévenin.
1. Déterminer le schéma équivalent de Thévenin pour chaque circuit.
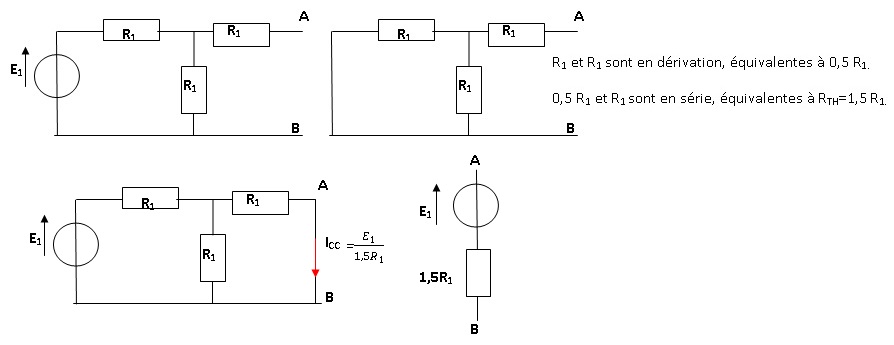
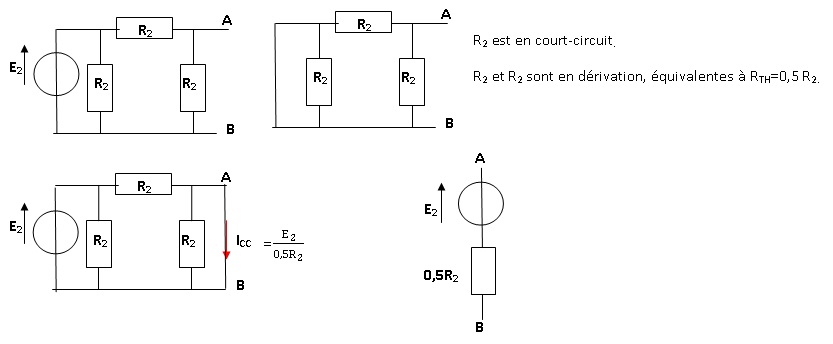 . .
2. Quelles relations doit-on avoir entre E1, E2, R1, R2 pour que ces deux circuits soient équivalents ?
E1 = E2 et 1,5 R1 = 0,5 R2.
|
|
|
|