Radioactivité,
mécanique, Doppler, induction, électronique,
concours EMIA 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Désintégration du potassium 40 en argon 40.
1. Donner la
signification de 4019K.
Le noyau de potassium compte 19 protons et 40-19 = 21 neutrons.
2.
Ecrire l'équation de cette réaction nucléaire. Quelles lois sont
utilisées ? De quel type de radioactivité s'agit-il ?
4019K ---> 01e
+4018Ar.
Conservation de la charge : 19 = 1 +18 ; conservation du nombre de
nucléons : 40 = 0 +40.
Radioactivité de type ß+ : émission d'un positon.
3. On donne la période radioactive
du potassium 40 : t½ = 109 ans.
a. Qu'appelle -ton
période radioactive ?
La période radioactive est la durée au bout de laquelle la moitié des
noyaux initiaux se sont désintégrés.
b. Exprimer en fonction du temps, le
nombre d'atomes de potasssium 40 ( NK) et d'argon ( NAr)
présents à une date t dans un échantillon contenant initialement N0
atomes de potassium 40.
NK = N0 exp(-l t) avec l t½ = ln(2).
NAr = N0-NK = N0(1-exp(-l t).
4.
Les cendres retrouvées sur un site contenaient du potassium 40. Au
moment de sa formation, cette cendre ne contenait pas d'argon ( gaz
volatil). L'âge de cette cendre est estimé à 3,7 millions d'années.
Quel est le rapport entre le nombre d'atomes d'argon 40 et le nombre
d'atomes de potassium 40 ?
NAr
/ NK = (1-exp(-l t) /
exp(-l t) = exp(l
t)-1.
lt
= ln(2) t / t½ =ln(2) x3,7 106 / 109=2,56
10-3.
NAr / NK =2,57 10-3.
Mécanique : voyage terre-lune.
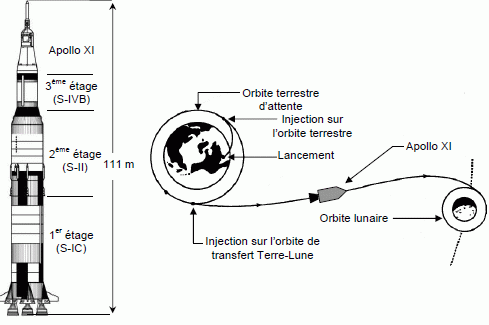 Le
premier étage de la fusée saturn V fonctionne pendant 160 s, il
contient environ 2 t de carburant et d'oxygène liquide permettant de
propulser la fusée à une altitude de 56 km. L'intensité supposée
constante de la force de poussée F des réacteurs est de 3,3 107
N.
Le
premier étage de la fusée saturn V fonctionne pendant 160 s, il
contient environ 2 t de carburant et d'oxygène liquide permettant de
propulser la fusée à une altitude de 56 km. L'intensité supposée
constante de la force de poussée F des réacteurs est de 3,3 107
N.
1.
Si on néglige "l'effet de fronde" quel référentiel supposé galiléen
peut-on choisir pour étudier dette première phase du mouvement ?
On peut utiliser un référentiel terrestre ou le référentiel
géocentrique au début du lancement.
2 :Faire
un inventaire des forces extérieures appliquées à la fusée en tenant
compte de
l’interaction de l’air avec la fusée. Les représenter au centre
d’inertie de la
fusée sur un schéma sans souci d’échelle (le décollage est supposé
vertical).
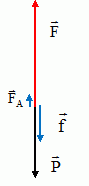
Le
poids P, la poussée des moteurs F, les forces de frottements f sur les
couches d'air, la poussée d'Archimède FA due à
l'air.
3. Après avoir énoncé la seconde loi
de Newton, expliquer pourquoi
ne peut-on pas l' appliquer , telle qu’elle est
énoncée, à
la fusée lors de son ascension ?
Dans
un référentiel galiléen, la somme vectorielle des forces extérieures
appliquées au système est égale à la masse du système multipliée par le
vecteur accélération de son centre d'inertie.
Les moteurs consomment du carburant et du comburant ( dioxygène liquide
) au décollage : la masse de la fusée n'est pas constante.
4. Quelle
hypothèse peut-on, cependant, poser pour appliquer cette loi au tout
début du
lancement ?
Sur une durée aussi petite que possible, la masse de la fusée est
à peu près constante.
5. En ne considérant
que le poids et la poussée, calculer la valeur de
l’accélération de la fusée à l’instant initial du lancement.
Masse de la fusée au moment du décollage
3037 t.
On écrit la seconde loi de Newton sur un axe orienté
vers le
haut : F-P = M a.
F-Mg=Ma ; a = F / M -g
; M =
3,037 x
10 3 tonnes =3,037 106 kg.
a = 3,3 x 10 7
/ ( 3,037 106
)-9,8 =1,067 ~1,07 m s-2.
Mise
en orbite autour de la
Terre du système {S-IVB +
Apollo XI}
A 68 km d’altitude,
les
réservoirs vides du premier étage sont largués et les cinq moteurs du
deuxième
étage sont allumés pendant 400 s. Après largage du deuxième étage,
l’unique
moteur du troisième étage est mis en fonction pendant 140 s permettant
la
satellisation sur une orbite circulaire d’attente à l’altitude h = 180 km.
Dans la
suite, on note {S} le système formé du troisième étage
et du vaisseau Apollo XI.
On étudie le
mouvement du système {S}, de centre
d’inertie G et de
masse m=120 t, dans le référentiel géocentrique supposé galiléen. On ne
tiendra
compte que de l’attraction gravitationnelle exercée par la Terre sur le
système
{S}..
 6.
Donner la définition du référentiel géocentrique.
6.
Donner la définition du référentiel géocentrique.
Le référentiel
héliocentrique a pour origine le Soleil et des axes
pointant vers des étoiles lointaines qui paraissent fixes.
Le référentiel géocentrique a pour origine le centre de la Terre et
des axes parallèles à ceux du référentiel héliocentrique.
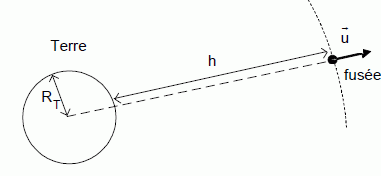
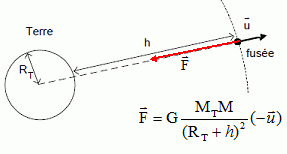
7. Donner
l’expression vectorielle de la force exercée par la Terre sur le
système
{fusée}
en utilisant le vecteur unitaire défini sur la
figure. Reproduire la figure sur la copie et représenter cette force
(sans souci d'échelle).
8. En appliquant la
deuxième
loi de Newton, établir l'expression vectorielle de l'accélération du
centre
d’inertie du système {fusée}. En supposant que le mouvement du système
{fusée}
est circulaire dans le référentiel géocentrique, montrer que le vecteur
accélération est centripète. En déduire que le mouvement est uniforme.
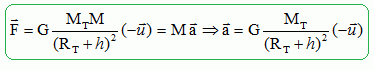
Le vecteur accélération est colinéaire au
vecteur unitaire et de sens contraire ; le vecteur accélération
étant dirigé vers le centre de la Terre est centripète.
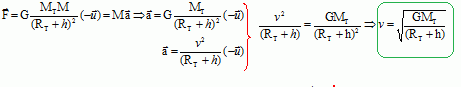
La valeur de la vitesse étant constante, le mouvement
est
uniforme.
9.
Calculer la
valeur de la vitesse du centre d’inertie G du système {S}.
RT+h =6,37 x
10 3 +180 km =6,55 106 m
v =[6,67 10-11
*5,98 x
10 24 / 6,55 106]½=7,80 103
m/s = 7,80 km/s ~
7,8 km/s.
Une
fois placée en orbite basse la système effectue un tour et demi autour
de la terre. Puis le moteur du troisième étage est allumé pour injecté
l'ensemble sur une orbite de transfert vers la lune. Une fois arrivé à
proximité de la lune, le moteur du module de commande est allumé pour
freiné la descente. Si ce freinage n'est pas réalisé, la trajectoire
permet au vaisseau de revenir se placer en orbite terrestre après avoir
fait le tour de la lune sans utiliser ses moteurs. Pour quelle mission
Appolo cette disposition a-t-elle été fort utile ?
Appolo 13, suite à l'explosion d'un réservoir d'oxygène.
|
|
|
Physique des ondes.
On cherche à déterminer la vitesse d'un véhicule de police se déplaçant
sirène hurlante. La sirène émet un son de fréquence f = 580 Hz. Le
véhicule se déplace vers la droite à la vitesse v.
1. Généralités sur
les ondes.
1.1 Définir une
onde mécanique progressive
.Une onde mécanique progressive est la propagation d'une perturbation
dans un milieu matériel sans transport de matière, mais avec transport
d'énergie.
1.2. Pourquoi une
éventuelle communication par onde sonores entre la terre et la lune ne
serait-elle pas possible ?
Les ondes sonores ne se propagent pas dans le vide.
1.3 Donner un
exemple d'onde pouvant se déplacer dans le vide.
Les ondes électromagnétiques.
1.4
Dans le cas d'une onde sonore, la direction de la perturbation est
parallèle à celle de la direction de la propagation. Comment peut-on
qualifier ces ondes ?
Ondes mécaniques longitudinales.
2. Dans un premier
temps, le véhicule se rapproche d'un observateur immobile..
Pendant l'intervalle de temps T, le son parcourt la distance l. Pendant ce temps le
véhicule parcourt la distance d = vT. La longueur d'onde l' perçue par l'onbservateur
à droite de la source S a donc pour expression l' = l -vT.(1).
2.1. Rappeler la relation liant la
vitesse de propagation c d'une onde, la longueur d'onde et la fréquence.
l = c
/ f.
2.2 La relation (1)
permet d'écrire f ' = f c / (c-v). f ' étant la fréquence sonore perçue
par l'observateur.
2.3. Le son perçu
est-il plus grave ou plus aigu ? Justifier.
c / (c-v) est supérieur à 1 ; f ' est donc supérieure à f : le son
perçu est plus aigu.
3. Dans un deuxième temps, le véhicule s'éloigne de l'observateur à la
même vitesse v.
3.1 Donner sans
démonstration, les expressions de la nouvelle longueur d'onde et de la
nouvelle fréquence perçue par l'observateur.
l ''=
l +vT. f '' = f c / (c+v).
3.2.
Le son perçu est-il plus grave ou plus aigu ? Justifier.
c / (c+v) est inférieur à 1 ; f '' est donc inférieure à f : le son
perçu est plus grave.
4. Exprimer en km /
h, la vitesse du véhicule qui se rapproche de l'observateur sachant que
ce dernier perçoit un son de fréquence f ' = 610 Hz.
f ' = f c / (c-v) ; f ' (c-v) = f c ; f c
/ f ' = c-v ; v = c(1-f / f ') = 340(1-580 / 610) =16,7 m/s
ou 16,7 x3,6=60,2 km /h.
5. Quel nom porte le phénomène mis
en évidence ? Effet Doppler.
|
|
|
|
Cinématique
du point.
Un
nageur parti de A se déplace à la vitesse V par rapport à l'eau d'une
rivière de largeur d. On suppose que le courant de cette rivière
possède une vitesse constante Ve par rapport aux berges. Ve
< V.
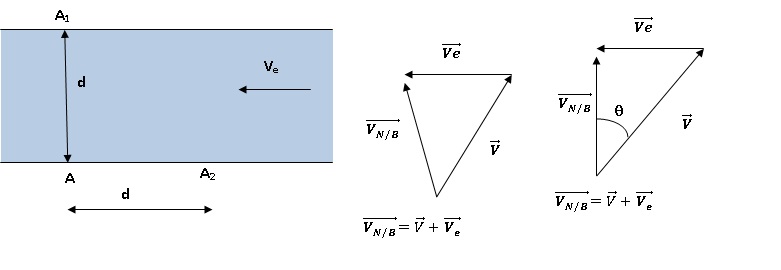
Partie I . Le
nageur effectue les trajets aller-retour AA1A en un temps t1
et AA2A en un temps t2.
1. Rappeler les
caractéristiques d'un vecteur. Donner les caractéristiques du vecteur
vitesse de l'eau par rapport à la berge.
Un vecteur est défini par son point d'application, sa direction, son
sens et sa norme. Le vecteur vitesse de l'eau est
horizontal, dirigé vers la gauche, de norme Ve .
2. Donner une
relation entre la vitesse du nageur par rapport à l'eau, la vitesse de
l'eau par rapport à la berge et une troisième vitesse que vous
définirez. Représenter graphiquement cette relation.
On note VN/B, la vitesse du nageur par rapport à la berge.
Voir ci-dessus.
3. Exprimer t1
en fonction de d, V et Ve.
VN/B est perpendiculaire à la rive.
VN/B =(V2-Ve2)½.
t1 = 2d / (V2-Ve2)½.
4. Exprimer t2 en
fonction de d, V et Ve.
A l'aller, VN/B a même direction et même sens que Ve,
au retour VN/B a même direction et le sens contraire de Ve
:
t2 = d /(V+Ve) +d / (V-Ve)=2Vd /
[(Ve+V)(V-Ve) ]= 2Vd / (V2-Ve2).
5. Exprimer le
rapport t2 / t1 en fonction de Ve/V.
t1 / t2 =(V2-Ve2)½
/ V = [1-(Ve/V)2]½ .
6. Sachant que t2
= 2t1
= 7 min, déterminer la direction de la vitesse V du nageur par rapport
à la berge qui se déplace à contre-courant pour atteindre A1
et le temps t0 qu'aurait mis le nageur pour parcourir
l'aller-retour AA1A en absence de courant. Ve = 1,8 km/h. d
= 98 m.
0,25=1-(Ve/V)2 ; (Ve/V)2 =0,75 ; Ve/V=0,866 ; sin
q
=0,866 ; q =60°.
t0 = 2d /V avec V = 1,8 / 0,866=2,078 km/h ou 2,078 /
3,6=0,577 m/s.
t0 =2 x98 / 0,577=339,5 s ou 5 min 40 s.
Partie II.
Le nageur quitte le bord A au moment où il se trouve à la distance d de
l'avant d'un bateau, de largeur L, qui se déplace à la vitesse
constante U par rapport à l'eau, en suivant le bord de la rivière dans
le sens A vers A2.
7. Faire un schéma
illustrant le problème en indiquant la trajectoire du nageur pour
éviter le bateau.
8. Déterminer la
direction et la grandeur de la vitesse absolue minimale du nageur pour
éviter le bateau. L = 20 m ; U = 19,8 km/h.
9. Déterminer alors
la direction et la grandeur de la vitesse V du nageur par rapport à
l'eau.
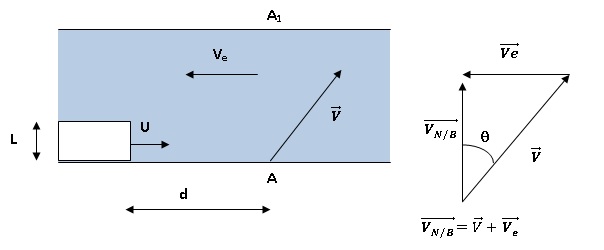
Vitesse du bateau par rapport à la berge : UB/B =U-Ve. Le
bateau parcourt la distance d en t seconde : t = d /(U-Ve).
Vitesse du nageur par rapport à la berge VN/B. Le nageur
parcourt la distance L en t' seconde : t' = L / VN/B.
Le nageur évite le bateau si t' < t : L / VN/B <d /(U-Ve)
; VN/B >L(U-Ve) /d = 20(19,8-1,8) / 98 = 3,67 km/h.
V = [V2e +V2N/B ]½= [1,82
+3,672 ]½=4,09 km/h.
sin q = Ve / V
= 1,8 / 4,09 = 0,440 ; q=26°.
|
|
Induction électromagnétique.
Un conducteur de L=40 cm de longueur se déplace en glissant sur un
circuit fermé à vitesse constante v= 3 m/s. L'ensemble est placé dans
un champ ùmagnétique uniforme perpendiculaire au plan contenant le
circuit et le barreau de norme B = 0,05 T.
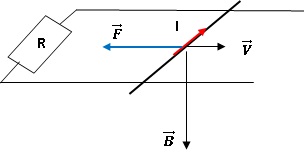
1. Quel est le champ électromoteur magnétique induit dans le barreau ?
La fem induite e associé au champ
électromoteur est égale à la
circulation du champ électromoteur sur le circuit
C.
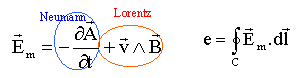 ; Em = v B = 3 x0,05 = 0,15 V m-1. ; Em = v B = 3 x0,05 = 0,15 V m-1.
2. Quelle est la fem induite dans le barreau ?
e = -dF /dt avec dF =B Lvdt, flux coupé pendant la durée dt.
e= -BLv = -0,05 x0,40 x3 = -0,06 V.
3.On note R =0,1 ohm la résistance du circuit, quelle est la valeur du courant
induit ?
i = -e /R = -0,06 / 0,1 = -0,6 A. Le signe indique que le courant induit a le sens contraire de I.
4. Quelle force faut-il exercer sur le barreau pour lui conserver une
vitesse constante ?
Le sens du corant induit est tel que par ces effets
électromagnétiques il s'oppose au
déplacement de la barre. La force de Laplace induite
est colinéaire à la vitesse mais de sens
contraire.
F = i LB = 0,6 x0,40 x0,05 = 0,012 N.
5. Quelle puissance mécanique doit-on fournir ?
Fv = 0,012 x3 = 0,036 W.
6. Quelle puissance électrique récupère-t-on ?
Puissance électrique totale : e i = 0,06 x0,6 = 0,036 W.
Puissance dissipée par effet Joule Ri2 = 0,1 x0,62 = 0,036 W.
Electronique.
1. L'association de la source idéale de tension de fem E1 et de la résistance R1 modèlise quel type de dipôle réel ?
Générateur réel de tension.
2. Déterminer l'intensité i dans la résistance R3 :
2.1 à partir du théorème de Millman ou du principe de superposition.
2.2 A partir du théorème de Thévenin ou de Norton.
A.N : R1 = 20 ohms ; R2 = 50 ohms ; R3 = 100 ohms ; E1 = 4 V ; I2 = 1 A.
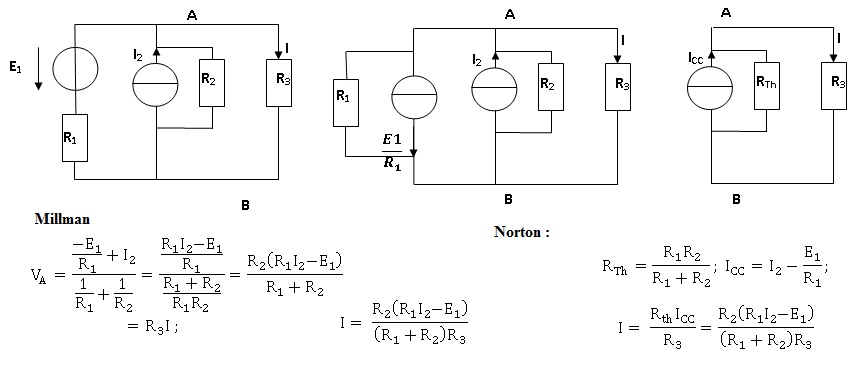
I = 50 x(20-4) / ((20+50) x100)=0,114 A.
Montage avec amplificateur opérationnel idéal.
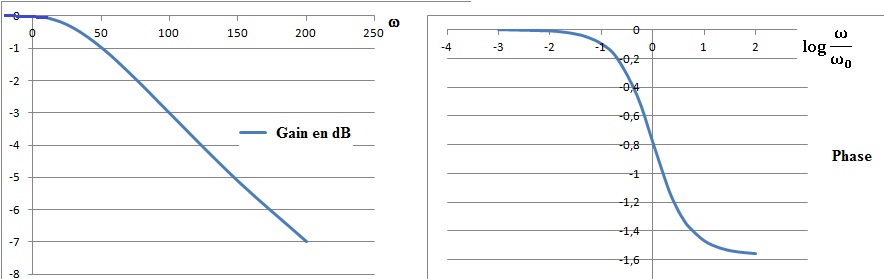
1. Calculer la fonction de transfert H(jw).
2. En déduire le gain et la phase.
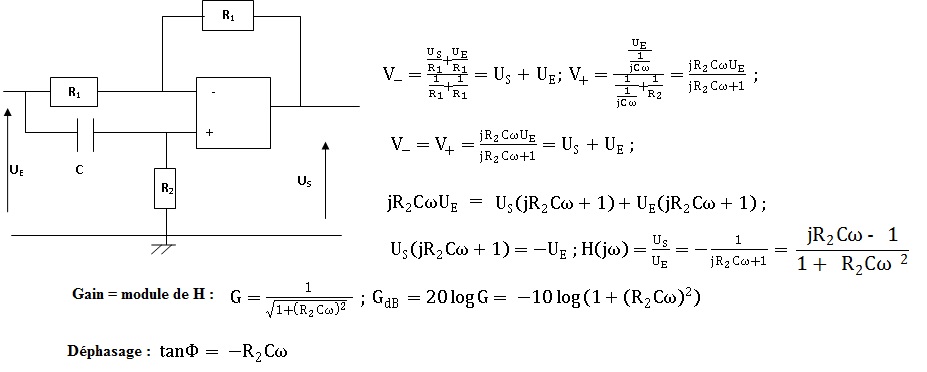
3. Tracer le diagramme de Bode. A quoi peut servir ce montage ?
Filtre passe bas actif du premier ordre.
4. Calculer l'impédance d'entrée du montage.
L'impédance d'entrée est égale à la tension d'entrée divisée par l'intensité d'entrée.
En basse fréquence, le condensateur se comporte comme un interrupteur ouvert.
L'impédance d'entrée est égale à l'impédance de la résistance d'entrée R1.
|
|




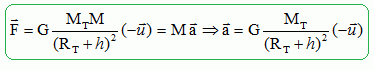
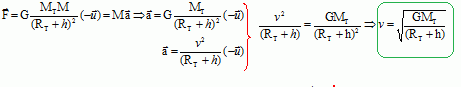



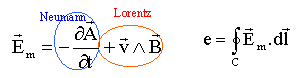 ; Em = v B = 3 x0,05 = 0,15 V m-1.
; Em = v B = 3 x0,05 = 0,15 V m-1.

