Voiture soumise à
une puissance constante, suspension Concours CGE 2010
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
1.
La voiture réduite à un point matériel.
On considère un véhicule, assimilé à un point matériel de masse m, en
mouvement rectiligne horizontal. Sa position est repérée par son
abscisse x et on ne considérera que les composantes des forces
colinéaires au vecteur directeur de l’axe Ox.
Dans tout le problème, on se place dans le référentiel terrestre
supposé galiléen.
1.1. L’automobile
n’est soumise qu’à l’action de son moteur qui développe une puissance
constante P. Elle part du repos en x = 0. Les frottements sont négligés.
Déterminer, en fonction du temps, les expressions de la vitesse v(t),
de l’accélération g(t), de
l’abscisse x(t).
La voiture est soumise à son poids, à l'action du sol opposée au poids
et à la force motrtice F horizontale et constante. Entre o et t, seule
la force motrice travaille.
Ecrire le théorème de l'énergie cinétique entre 0 et t : Pt = ½mv2
; v =( 2Pt / m)½.
L'accélération est la dérivée de la vitesse par rapport au temps : g = dv
/dt=( P / (2mt))½.
La position est une primitive de la vitesse et si on chosit l'instant
initial à l'origine des abscisses :
x=2 /3 ( 2P / m)½ t1,5.
1.2. Déterminer
l’expression de x en fonction de la vitesse v.
v2 = 2Pt / m ; t = mv2/ (2P) ; repport dans
l'expression de x :
x2 = 4/9 2P / m [mv2/(2P)]3 = m2v6
/ (9P2) ; x = mv3/(3P).
1.3. Au bout de
quelle distance le véhicule aura-t-il atteint la vitesse de 90 km/h ?
On donne : m = 1200 kg et P = 75 kW.
v=90/3,6=25 m/s ; P = 75000 W.
x = 1200 *253/(3*75000)=83,3 m.
1.4. La voiture est
maintenant soumise, en plus de l’action du moteur, à une force de
résistance de l’air, de norme k m v2, où k est une constante
positive.
1.4.1. En utilisant
le théorème de l’énergie cinétique, pendant une durée infinitésimale
dt, établir l’équation différentielle : dx =mv2dv / (P-kmv3).
Entre les instant t et t+dt : ½m(v+dv)2-½mv2 =
Pdt - kmv2dx = Pdt-kmv3dt = (P-kmv3)dt.
En négligeant le terme du second ordre dv2 :
mvdv=(P-kmv3)dt avec dx = vdt.
mv2dv=(P-kmv3)dx
; dx = mv2dv / (P-kmv3).
1.4.2. En intégrant cette équation
différentielle, exprimer x en fonction de v, sachant que x(0)=0 et
v(0)=0.
On pose u =P-kmv3 ; du = -3kmv2dv d'où : dx =du/
(-3ku)
Intégrer : x = -1/(3k) lnu +cste ;
xt=0)=0 = -1/(3k) ln P +cste ; cste =
1/(3k) ln P.
x = 1/(3k)[ ln P-ln(P-kmv3)]
x= 1/(3k) ln( P /(P-kmv3)).
1.4.3. Montrer
qu’il existe une vitesse limite Voo.
e3kx=P / (P-kmv3) ; P-kmv3 =
Pe-3kx.
Quand x devient grand, e-3kx tend vers zéro.
P-kmvoo3
=0 ; voo =[P /(km)]1/3.
1.4.4. Donner x en fonction de v et
de Voo.
x=1/(3k) ln( 1 /(1-(v/voo)3)).
1.5. On donne Voo = 180
km/h. (180/3,6)=50 m/s.
1.5.1. Calculer la
valeur de k.
k =P /(mvoo3)=75000 /(1200*503)=5 10-4m-1.
1.5.2. Au bout de quelle distance X,
le véhicule aura-t-il atteint la vitesse de 90 km/h ?
x=1/(3k)
ln( 1 /(1-(v/voo)3))=1/ (1,5 10-3) ln(1/(1-0,53))=89
m.
|
|
|
1.6. Pour déterminer l’accélération
de l’automobile, on utilise un accéléromètre hydrostatique.
Il est constitué d’un tube en U, de faible section S, rempli d’un
liquide de masse volumique μ.
On l’accole solidairement à la carrosserie de sorte qu’il subit la même
accélération constante et horizontale γ que la voiture.
On constate une différence de niveau entre les surfaces libres A et B
du liquide.
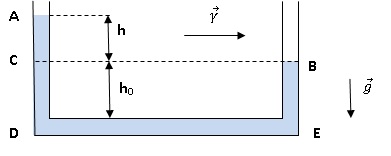
On
donne : L = 12 cm = DE, g = 10 m/s² et h = 3 cm.
1.6.1. Calculer la
différence de pression DP
= PD – PE.
DP
= µgh
1.6.2. En déduire la force qui agit
sur la colonne horizontale de liquide entre D et E.
F = DP S = µgh S
1.6.3. Montrer que l’accélération de
l’automobile s’écrit g
= g h / L. Calculer sa valeur.
F = m g avec m =
SL µ ; F = SL µ g.
SL µ g = µgh S ;
g = g
h / L=10*12/3=40 m s-2.
|
|
|
|
Etude de la suspension.
On considère le système (S) formé par le quart de la
voiture de centre de masse G et décrit ci-dessous.
On supposera que (S), de masse m = 300 kg, n’est pas couplé avec le
reste de l’automobile.
Le point O correspond à la position de G lorsque le système (S) est
immobile par rapport à l’axe vertical Oz.
Le système (S) est relié au sol par un ressort (R) de raideur k = 22
kN/m et il est soumis de la part d’unamortisseur (A), à une force de
frottement fluide f avec μ = 800 kg/s.
Dans tout le problème, la voiture roule sur une route horizontale avec
une vitesse constante.
La voiture rencontre une bosse à l’instant initial. À cet instant z(0)
= z0 = 5 cm et (dz/dt) (0)= 0.
4.1. Écrire
l’équation du mouvement vertical de G, satisfaite par z(t).
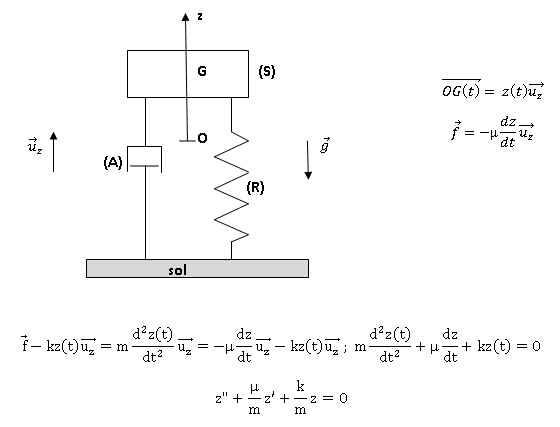
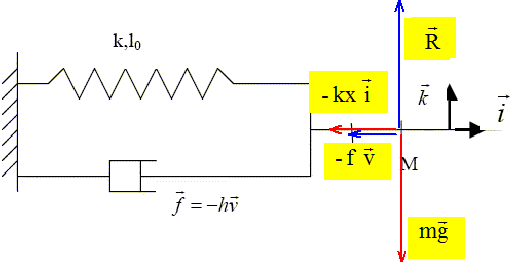
4.2. Montrer, en
utilisant les valeurs numériques, que le mouvement de G est
pseudo-périodique.
µ / m = 800 / 300= 8 / 3 ~2,67 s-1 ; k/m=22000 /300
=73,3 s-2.
Equation caractéristique : r2 +2,67 r +0,0733=0
Discriminant : 2,672-4*73,3 ~-286.
Le déterminant étant négatif, il n'y a pas de racine réelle. Le
mouvement est donc pseudo-périodique.
4.3. La fonction z
étant alors de la forme z(t) = A exp(-at) cos(wt + F), donner l’expression de a en
fonction μ et m ainsi que l’expression de w en fonction de μ , m et k.
On pose a = µ / (2m) ; w02 =
k / m ; -D = 4(w02-a2)=4w2.
Solutions de l'équation caractéristique : a ±w.
w2 =k/m -µ2
/ (4m2)=k /m [1-µ2 / (4km)] = w02[1-µ2
/ (4km)].
w=w0[1-µ2
/ (4km)]½.
4.4. Calculer la
valeur numérique de la pseudo-période T du mouvement.
T = 2p /w ; w0 = (22000 / 300)½=8,56
rad / s.
µ2 / (4km) =8002 / (4*22000*300)=0,0242 ; [1-µ2
/ (4km)]½=0,9878 ; w=8,56*0,9878=8,46
rad/s ; T = 6,28/8,46=0,743 s.
4.5. Exprimer A et
tan F en fonction
de z0, a
et w. Calculer
les valeurs numériques de A et F.
z(t) = A exp(-at)
cos(wt + F).
z(0) = A exp(0) cos(0 + F)
; z0=A cos(F).
vitesse z'(t) = -A exp(-at)
[acos(wt + F) + w sin(wt + F) ]
z'(0) = 0 = acos( F)+w sin( F) ; tan F = -a /w ;
a = µ /(2m) = 800/600=4 /3 ; w =8,46 rad / s ; tan F = -4/(3*8,46)= -0,1576 ; F = -8,96°.
cos2 F
= 1/(1+tan2F)
= 1/(1+a2/w2)=w2/ (a2
+w2).
z0=A cos(F)
; A= z0 (a2 +w2)½ /w.
cos(F) =0,9878 ; A
= 0,05 / 0,9878=0,0506 m.
4.6. La voiture
roule sur une route ne présentant pas de bosses. Les amortisseurs sont
déréglés.
Tout se passe comme si le système (S) ne subissait que les forces qui
s’exerçaient sur lui lors de l’étude précédente. Ces forces sont
inchangées ; par contre la valeur du coefficient μ est modifiée. La
voiture rencontre la même bosse à l’instant initial.
On s’intéresse toujours au mouvement vertical de G, qui est, à partir
de cet instant apériodique critique.
4.6.1. Quelle est
la relation entre m, k et μ ? En déduire la nouvelle valeur de μ .
Le discriminant de l'équation caractéristique est nul :
(µ / m)2 = 4k / m ; µ =2 (km)½ = 2(22000*300)½
=5138 kg / s.
4.6.2. Donner la
nouvelle expression de z(t) en fonction de z0 et w0 .
z(t)= zmax(1+at)exp(-at).
z(0)=z0 = zmax ; z(t)= z0(1+at)exp(-at).
.
|
|
Allumage automatique des feux de position.
L’automobile est munie d’un allumage automatique des
feux de position. Celui-ci se fait en fonction de
l’éclairement extérieur E, et est réalisé grâce au circuit
ci-dessous comprenant un amplificateur
opérationnel (AO) et une diode (D).
L’amplificateur
opérationnel est considéré comme parfait et fonctionne en régime
linéaire.
La diode (D) est une photodiode. Polarisée en sens inverse, elle est
parcourue par un courant dont l’intensité I ne dépend que de
l’éclairement E qu’elle reçoit. L’éclairement E se mesure en W/m².
On donne : I = I0 + a E avec I0 = 4 μA, a = 65x10-9
SI et R = 10 kΩ.
3.1. Exprimer le
gain G = Us/Ue en fonction de R1 et R2.
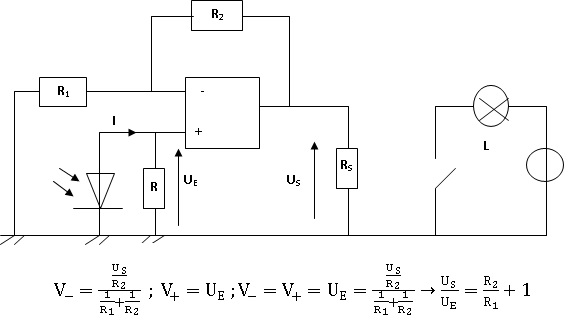
3.2. Quelle valeur
faut-il donner au rapport R2 / R1 pour avoir G = 50 ?
50 = R2 / R1 +1 ; 49 = R2
/ R1.
3.3.
Exprimer UE en fonction de I, puis de E.
UE = RI =R(I0+aE).
3.4. Mettre Us
sous la forme : Us = U0 + KE. On donnera les
valeurs de U0 et K.
US = UE(R2/R1+1)=R(I0+aE)(R2/R1+1) = RI0
(R2/R1+1)+Ra(R2/R1+1)
E.
U0 = RI0
(R2/R1+1)=10
* 4 10-3 *50 =2 V ; K = Ra(R2/R1+1)=10*65 10-9
*50 =3,25 10-5V m2W-1.
3.5.
À la sortie de l’amplificateur opérationnel se trouve un relais
électromécanique qui s’enclenche si Us = 8 V, ce qui ferme
le circuit contenant une lampe à halogène (L).
Pour quelle valeur de l’éclairement le relais s’enclenche-t-il ?
Us = U0 + KE ; E =
(Us-U0) / K = (8-2) /(3,25 10-5) =1,85
105 Wm-2.
|
|