Neutron, neutrino,
relativité, pendule dans un wagon.
Concours Avenir 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
5.
Le neutron est une particule de masse m = 1,7 10-27
kg. Sur terre, il est présent dans le noyau de la plupart des
atomes mais il peut également exister de façon indépendante. Loius de
Broglie a démontré en 1924 que le mouvement d'une particule peut aussi
être assimilé à une onde nommée " onde de matière". h = 6,6 10-34
Js.
39. La relation
entre la longueur d'onde l
et la quantité de mouvement p est
:
lp=h, vrai ; l p h = 1, faux ; lh = p, faux ; l = hp, faux.
40. Un neutron " lent " a une
vitesse v = 2,0 km/s. Sa quantité de mouvement est ( en kg m s-1
) :
8,5 10-28 ; 3,4 10-27 ; 8,5 10-25 ; 3,4 10-24.
Vrai.
p = mv = 1,7 10-27 *2,0 103 = 3,4 10-24.
41.
La longueur d'onde de De Broglie est ( en m) :
1,9 10-13
; 1,9 10-10 , vrai ; 1,9 107 ; 1,9
1010.
h / p = 6,6 10-34 / (3,4 10-24) =1,9 10-10
m.
42.
On manipule maintenant un autre neutron, d'énergie cinétique 10 000
fois plus élevée que celle du neutron précédent. Sa vitesse vaut ( en
m/s) :
A . 2,0 105 , vrai ; B. 2,0 107 ; C.
2,0 108
; D. relativiste ( trop proche de la vitesse de la lumière dans le vide
pour être simplement calculée avec les formules de la mécanique
classique ).
Pour la mécanique classique, si l'énergie cinétique est multipliée par
10 000 , alors la vitesse est multipliée par 100 ( la masse restant
constante ).
2 103 *100 = 2 105 m/s.
43 . La longueur
d'onde de De Broglie associée à ce neutron rapide est :
A. plus courte que celle associée au neutron lent, vrai l = h / (mv) ;
B. égale à celle associée à un neutron lent ;
C. plus grande que celle associée au neutron lent ;
D. il manque une donnée pour comparer les deux longueurs d'onde.
Exercice 6.
Le neutrino est une particule électriquement neutre et très légère,
prédite par la théorie en 1930. Sa masse est estimée à 10-37
kg et sa vitesse est pratiquement égale à la célérité de la lumière
dans le vide. Sur terre, nous recevons chaque seconde, des milliards de
neutrinos provenant essentiellement du soleil. Ils nous traversent sans
être ralentis, comme si la terre était transparente. Seuls quelques uns
sont absorbés. On étudie la durée de propagation des neutrinos
provenant du soleil.
44.
La vitesse du neutrino dans le référentiel héliocentrique est ( en m
/s) :
2,97 105 ; 3,00 105 ; 2,97 108 ; 3,00 108, vrai.
45. La distance terre soleil est
d'environ ( en m) :
1,5 106 ; 1,5 108 ; 1,5 109 ; 1,5 1011.
Vrai.
46. Dans le
référentiel héliocentrique, la durée du parcours du neutrino du soleil
à la terre est ( en s ) : 200 ; 500,
vrai ; 2000 ; 5000. .
1,5 1011 / (3,00 108)=500 s.
|
|
|
47. Chaque neutrino d'origine
solaire porte une énergie d'environ 10 MeV ( 1 eV = 1,6 10-19
J). Dans l'unité fondamentale, cette énergie vaut ( en J) :
1,6 10-13 ; 6,2 10-13 ; 1,6 10-12
, vrai ; 6,2 10-12.
10 *106 *1,6 10-19 = 1,6 10-12 J.
48. L'énergie des
neutrino permet d'estimer leur facteur relativiste g ~108. Quelle
est la seule affirmation vraie ?
A. La durée du parcours, dans le référentiel propre du neutrino est 20
µs.
500 / 108 = 5 10-6 s = 5 µs.
B. La
durée du parcours, dans le référentiel propre du neutrino est 2 1010
s.
C. Lorsqu'ils traversent les océans, les neutrinos sont plus rapides
que la lumière ( dans l'eau la vitesse de la lumière vaut 75 % de sa
valeur dans le vide ). Vrai.
D. Plus le facteur relativiste g
est grand, plus la célérité de la lumière dans le vide est faible dans
le référentiel propre du neutrino.
49. En astronomie "neutrino" on
s'intéresse aux neutrinos venant d'autres étoiles ou d'autres galaxies.
Il est possible d'identifier des neutrinos provenant du grand
nuage de Magellan, une galaxie située à 150 000 années de lumière de
nous ( soit une distance d = 1,4 1021 m ). Dans le
référentiel propre du neutrino, la durée du parcours est :
1,5 10-6 an = 47 s ; 1,5
10-5 an = 4,7 102 s ; 1,5 10-4 an = 4,7 103
s ; 1,5 10-3 an = 4,7 104 s, vrai.
Dt =( 1,4 1021
/ 3 108 )~ 4,7 1012 s ;
durée propre : Dt0
= Dt
/ g = 4,7 1012 / 108 =4,7
104 s.
Les
détecteurs à neutrinos actuels sont de grandes piscines d'eau pure,
profondément enterrées sous le sol. Un neutrino qui interagit avec la
matière se transforme en un muon ( particule semblable à un électron,
mais 200 fois plus lourde ) que l'on détecte parce qu'il provoque dans
l'eau une traînée de lumière. Le muon est instable : en moyenne sa
durée de vie propre est de l'ordre de 2 µs. Des mesures ont permis
d'établir sa vitesse dans le référentiel du laboratoire vmuon
/ c = ~0,87~(3 / 4)½.
50.
Dans le référentiel du laboratoire, la distance moyenne parcourue par
le muon avant de se désintégrer est d'environ ( en km ) : 1 , vrai; 10 ; 100 ; 1000.
g =
[1-(vmuon/c)2]-½ ~ [1-3 /
4]-½ ~ [1 / 4]-½
~2
Durée
mesurée : 2*2 = 4 µs. 4 10-6 * 0,87 *3 108 ~ 103
m ~ 1 km.
|
|
|
|
Exercice 7. 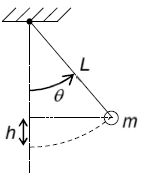
Dans
un wagon fermé, on fixe au plafond un pendule constitué d'un solide
supposé ponctuel, de masse m, libre d'osciller au bout d'un fil de
longueur L et de masse quasi-nulle.
51. La hauteur h entre la position du pendule ( à un instant quelconque où il est écarté de sa position d'équilibre d'un angle q par rapport à la verticale) et la position d'équilibre est :
L sin q ; L cos q ; L(1-sin q) ; L ( 1-cos q), vrai.
Pour les oscillations de faible amplitude, les oscillations sont décrites au cours du temps par une loi horaire de la forme q(t) = q0 cos ( wt) où q0 représente l'amplitude des oscillations et w leur pusation.
52. La loi horaire décrivant l'accélération angulaire du pendule est :
A. d2q / dt2 = w2q0 sin ( wt) ;
B. d2q / dt2 = -w2q0 sin ( wt) ;
C. d2q / dt2 = w2q0 cos ( wt) ;
D. d2q / dt2 = -w2q0 cos ( wt) ; vrai.
53. La période des oscillations du pendule est :
2p ( g / L)½ ; 2p ( L /g)½ , vrai ; 2p ( m / g)½ ; 2p ( m / L)½ .
54.
La période des oscillations de grande amplitude du pendule est indépendante de :
A. la masse du pendule ; vrai ;
B. l'amplitude des oscillations ; faux ;
C. la longueur du fil ; faux ;
D. la valeur du champ de pesanteur. Faux.
Le wagon est maintenant en mouvement circulaire
uniforme dans un virage. Dans le référentiel lié au wagon, le pendule
est maintenant à l'équilibre dans une position inclinée par rapport à
la verticale d'un angle ß = 6 °.
55. Dans le réfréentiel terrestre ( considéré comme galiléen ), les forces exercées sur la masse suspendue au bout du fil sont :
A. le poids uniquement, faux ;
B. le poids et la tension du fil, vrai ;
C. le poids, la tension du fil et les frottements de l'air, faux ;
D. le poids, la tension du fil, les frottements de l'air et la force centrifuge. Faux.
Dans le référentiel galiléen du wagon, une force supplémentaire apparaît, la force centrifuge. Elle s'exprime sous la forme Fc = mv2 /R ( v : vitesse du train, R rayon de la trajectoire circulaire ).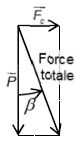
56. La relation entre ß, P et Fc est :
Fc = P sin ß ; Fc = P cos ß ; Fc = P tan ß vrai ; Fc = P cos ß / sin ß.
57. La vitesse du train est ( en m/s) : ( avec R = 400 m ; g = 10 m s-2 ; sin 6° ~0,10 ; cos 6° ~0,99 ; tan 6°~0,10 ).
9 ; 20 vrai ; 36 ; 64.
mv2/R = mg tan ß ; v2 = Rg tan ß = 400 *10 *0,10 = 400 ; v = 20 m/s.
58. Au cours du temps, l'énergie mécanique du pendule :
A. reste constante, faux ;
B. diminue à cause du travail du poids, faux ;
C. Diminue à cause du travail des forces de frottements, vrai ;
D. augmente, faux.
59. La loi horaire qui décrit les oscillations libres amorties du pendule est ( avec t une durée caractéristique) :
A. q(t) = q0 exp(-t / t).
B. q(t) = q0 sin ( 2pt / t) cos(wt).
C. q(t) = q0 exp(-t / t)cos(wt). Vrai.
D. q(t) = q0 exp(+t / t)cos(wt).
La mesure de la pseudopériode des oscillations libres amorties est une
autre méthode pour calculer la pesanteur "apparente" ressentie g' dans
le wagon. La mesure fournit T = 1,97 ±0,03 s. On mesure par ailleurs la
longueur du fil L = 1,000±0,002 m. On donne la relation permettant de
calculer l'incertitude relative Dg' / g' = DL / L + 2DT /T.
60. La valeur de la pesanteur apparente g', avec son incertitude , est ( en m s-2) :
10,1 ± 0,3 vrai ; 10,17 ±0,03 ; 10,172 ±0,003 ; 10,1724 ±0,0003.
g' = g / cos ß =10 / 0,99 ~ 10,1 m s-2.
Dg' / g' =0,002 + 0,06 / 1,97 = 0,032 ; Dg' = 10,1 *0,032 ~0,3 m s-2.
|
|