Ultrasons,
satellite.
Concours Avenir 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1.
L'échographie
est une technique d'imagerie médicale : des ultrasons sont envoyés dans
l'organisme par une sonde appliquée sur la peau. En changeant de milieu
de propagation ( en entrant ou en sortant d'un organe, par exemple ),
une partie de l'onde est réfléchie et retourne vers la sonde.
1. Les ultrasons sont
:
A) des ondes mécaniques progressives ; vrai
;
B. des ondes mécaniques stationnaires; faux ;
C. des ondes électromagnétiques progressives ; faux ;
D. des ondes électromagnétiques stationnaires
; faux.
2. Les
ultrasons :
A. se propagent plus rapidement dans les gaz que dans les liquides ;
faux ;
B. se propagent en ligne droite sauf quand ils sont réfléchis ;
faux ;
C. se propagent à la même vitesse que le son ( en considérant que dans
l'organisme les sons graves et aigus ont la même vitesse ) ; vrai ;
D. sont constamment
déviés, la diffraction étant dans ce cas plus importante que pour les
sons. Faux.
3. La
diffraction limite la taille des petits détails qu'il est
possible d'observer avec cette technique. Le demi-angle q de la tache centrale de
diffraction produite, quand une onde de longueur d'onde l arrive sur un objet de
diamètre a est :
a / l ; l / a ( vrai) ; l / a2 ; a2/l.
4.Les ultrasons utilisés ici
ont une fréquence de l'ordre de f = 10 MHz. Dans le corps humain (
majoritairement constitué d'eau ), leur célérité vaut v = 1500 m/s. La
longueur d'onde des ultrasons dans le corps humain est :
v f ; v / f, vrai ; f /
v ; 1 / (vf).
5. Les plus petits
détails observables produisent alors une tache de diffraction dont
l'angle q est de
l'ordre de 1 rad. La taille alimite des plus petits détails
observables est donc :
150 µm , vrai ; 1,5
mm ; 6,7 mm ; 1,5 cm.
l = v
/ f = 1500 / (10 106)=1,5 10-4 m ;
alimite =l
/ q = 1,5
10-4 / 1 = 1,5 10-4
m = 150 µm.
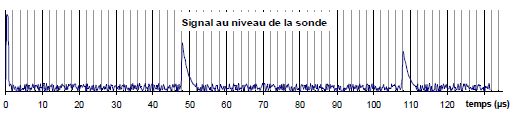
Pour permettre la mesure du signal renvoyé au niveau
de la
sonde, les ultrasons ne sont pas émis en continu : on envoie des salves
de durée très courte ( sur l'oscillogramme ci-dessous, c'est le premier
pic, à l'extrème gauche ). De cette façon on visualise clairement le ou
les échos qui reviennent au capteur ( ici, il y en a deux : les deux
pics reçus à 48 µs et à 108 µs). L'axe vertical du graphe correspond à
la tension aux bornes du capteur.
6.
Soit v la célérité des ultrasons et Dt la durée de propagation,
la distance d entre la sonde et l'objet sur lequel les ultasons sont
réfléchis, est :
v / Dt ; v / (2Dt) ; v Dt ; v Dt / 2,
vrai.
Distance aller + distance retour = 2 d = v Dt.
7.
Les deux échos correspondent ici auc ultrasons réfléchis à
l'entrée puis à la sortie d'un même organe. L'épaisseur e ( en cm ) de
l'organe mesurée dans la direction de propagation de l'onde est : 1,2 ;
2,5 ; 4,5, vrai ; 9,0.
e = ½*1500 ( 108-48) 10-6 = 4,5 10-2 m = 4,5 cm.
|
|
|
L'échographie
peut aussi être associée à un capteur Doppler. Il est alors possible de
détecter et de localiser d'éventuels caillots ( thrombose ) dans les
vaisseaux sanguins. En effet, un caillot provoque un rétrécissement qui
entraîne une augmentation locale de la vitesse de l'écoulement du sang.
Quand la sonde envoie des ultrasons, les globules rouges du sang, qui
se déplacent à la vitesse vglob réfléchissent eux aussi les
ultrasons et les renvoient vers la sonde.
8. Du fait de
l'effet Dopler, la longueur d'onde lR des ultrasons
qui reviennent au capteur est :
A. inférieure à la longueur d'onde propre émise l0 ;
B.
supérieure à la longueur d'onde propre émise l0 ;
C. invariante danc égale à la longueur d'onde émise ;
D. tout dépend de l'orientation de la sonde par rapport au vaisseau
sanguin. Vrai.
En pratique, on ne mesure pas diectement l'écart entre la fréquence
reçue et la fréquence émise. Il est plus simple d'additionner l'onde
émise et l'onde reçue. On obtient alors des battements, c'est à dire un
signal dont l'amplitude varie périodiquement ( le graphe ci-dessous
représente en abscisse le temps et en ordonnée la tension totale aux
bornes du capteur ).
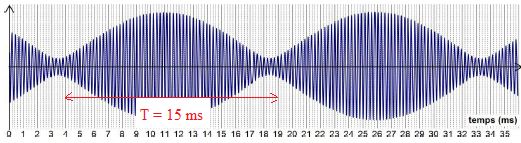
9.La période Tbatt
des battements est ( en ms) :
0,23 ; 3,4 ; 15 ( vrai) ; 30.
La vitesse des globules rouges est donnée par la relation vglob
= v Df / 2f où v
est la célérité des ultrasons, f leur fréquence et Df le déclage en fréquence
dû à l'effet Doppler.
Par ailleurs la période des battements est donnée par Tbatt
= 2 / Df.
On donne v = 1500 m/s et f = 10 MHz.
10.
La vitesse des globules rouges est ( en cm/s) : 1,0 ( vrai) ; 6,7 ; 10 ; 67.
Df
= 2 / Tbatt = 2 /(0,015) =133,3 Hz ; vglob
= v Df / 2f
= 1500 *133,3 / (20 106) =1,0 10-2 m/s = 1,0 cm/s.
|
|
|
|
Exercice 2.
On veut placer un satellite de1,6 tonnes sur une orbite
géostationnaire, c'est à dire une orbite circulaire pour laquelle
le satellite se trouve à tout moment à la verticale du même point
de la terre. On donne l'énergie potentielle de gravitation Ep
d'un corps de masse m à la distance r du centre de la terre : Ep
= -GmM / r ( supposée nulle à distance infinie ) avec M masse de la
terre et G la constante de gravitation universelle.
On prendra GmM ~6,5 1017 SI.
11. Dans le système
internationnal, la grandeur GmM peut d'exprimer en :
J m ( vrai) ; J m2
; Jm-1 ; J m-2.
12. En orbite
géostationnaire, un satellite fait un tour de la terre en :
88 min ; 104 min ; 24 heures (
vrai) ; 1 an.
Mouvement rectiligne uniformément
accéléré.
13.
En orbite géostationnaire, le vecteur accélération du satellite, dans
le référentiel géocentrique, est :
A. orienté vers le centre de la terre ; vrai ;
B. orienté tangentiellement à la trajectoire, vers l'avant ;
B. orienté tangentiellement à la trajectoire, vers l'arrière ;
D. orienté en biais ( une composante tangentielle et une composante
radiale).
14.
La vitesse d'un satellite sur une orbite circulaire de rayon R et de
période T est :
RT / (2p ) ; 2pT/R ; 2pR / T, vrai ; aucune de ces
relations, elle varie au cours du temps.
15. Au cours du
lancement, on
installe dans un premier temps le satellite sur une orbite circulaire
provisoire, à 120 km d'altitude ( soit R = 6500 km). D'après la 3è
loi de Kepler, la période orbitale du satellite est alors :
[ R3 4p2 /
(GM)]½, vrai ; [ R3 4p2 / (GM)]1/3
; [ 4p2 / (R3GM)]½, [ 4p2
/ (R3GM)]1/3.
16. L'énergie
cinétique du satellite en orbite circulaire à 120 km d'altitude est Ec
= 5 1010 J. Son énergie mécanique est ( en J) :
-1 1011 ; -5 1010 ( vrai) ; 5 1010 ; 1 1011.
Ep
= -GmM / R = -6,5 1017 / (6500 103) = -1,0 1011
J.
Em = Ec + Ep = -5 1010 J.
On veut maintenant modifier l'orbite du satellite. POur cela, on
augmente quasi instantanément sa vitesse ( en allumant son
réacteur ). Le satellite passe ainsi d'une vitesse v1 = 7,8
km/s à une vitesse v2 ( dont il s'agira de déterminer la
valeur ) en une durée très réduite ( en pratique Dt
= 50 s). Sa trajectoire devient alors une ellipse : au plus près de la
terre il est toujours à l'altitude de 120 km, mais au plus loin, il
passe à 35 800 km d'altitude ( R' = 42 200 km du centre de la terre).
17. Pendant le
passage de v1 à v2, l'accélération due au moteur
du satellite est constante et vaut a = 50 m s-2. La valeur
de v2 est ( en km/s) :
7,9
; 8,3 ; 9,3 ; 10,3. Vrai.
a =(v2-v1) / Dt ; v2=v1
+a Dt= 7800
+50*50 =10,3 103 m/s = 10,3 km/s.
Pendant cette
phase d'accélération le satellite perd une masse Dm
de combustible. Les gaz de combustion sont éjectés par une tuyère à la
vitesse w = 2,4 km/s par rapport au satellite. On notera 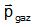 la
quantité de mouvement totale des gaz éjectés, la la
quantité de mouvement totale des gaz éjectés, la 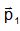 quantité de
mouvement du satellite à la vitesse v1 et quantité de
mouvement du satellite à la vitesse v1 et 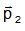 sa
quantité de mouvement à la vitesse v2. sa
quantité de mouvement à la vitesse v2.
La durée de la phase d'accélération étant courte, ces vecteurs sont
supposés colinéaires.
18. L'ensemble {satellite + gaz éjectés} formant un système
isolé, la relation entre les vecteurs quantités de mouvement est :
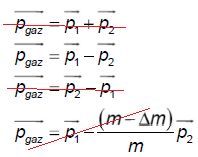
Conservation de la quantité de mouvement du système :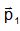 = =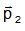 + +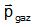 . .
19. En projetant cette relation sur l'axe portant les vecteurs, la relation devient, Dm étant positive :
A. Dm (w+v2) = m(v2-v1). Vrai.
mv1 = -Dmw +(m-Dm)v2.
Dm (w +v2)= m(v2-v1).
B. Dm (w-v2) = m(v2+v1).
C. Dm (w+v2) = m(v2+v1).
D. Dm (w-v2) = m(v2-v1).
20. La masse ejectée par le satellite ( en %) est :
Dm / m < 5 % ; 5 % < Dm / m < 15 % ; 15 % < Dm / m < 25 % , vrai ; 25 % < Dm / m < 35 %.
Dm / m = (v2-v1) / (w+v2) = (10,3-7,8) / (10,3+2,4) ~0,20 ( 20 %).
On repète l'opération lorsque le satellite atteint l'altitude voulue.
Une deuxième phase d'accélération permet de le stabiliser sur l'orbite
géostationnaire en lui donnant sa vitesse définitive.
|
|