Optique, ondes à la surface de l'eau, se protéger du bruit. Concours Caplp maths sciences 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Phénomènes optiques. L’enseignant aborde le module SL1 « Comment dévier la lumière ? » avec sa classe. C.1.1. Le document ci-dessous sert de support à sa première séance. Formuler une question de type « situation déclenchante » qui pourrait accompagner ce document. Proposer, sous la forme d’un tableau clair et concis, un déroulement de séance correspondant à son exploitation en classe. La vision dans l'air est-elle identique à la vision sous l'eau ? Dans l'air, l'image d'un objet éloigné se forme sur la rétine ; sous l'eau, sans masque, elle se forme derrière la rétine. La vision sous l'eau n'est pas nette. La lumière solaire subit des modifications en passant sous la surface. - 5 % des rayons incidents sont réfléchis ; - le passage d'un rayon lumineux de l'air dans l'eau se traduit par un changement de direction, perçu par le plongeur comme une déformation des images ( un bâton semi-immergé paraît brisé lorsqu'on le regarde depuis la surface) ; - la vision des couleurs est modifiée, le rouge étant rapidement absorbé. La correction de la vision peut être réalisée par le port d'un masque, créant une interface "eau /air / cornée " ; le pouvoir convergent de la cornée est ainsi rétabli. La vision est nette à la fois en surface et dans l'eau, mais l'appréciation des distances est modifiée, la taille des images est augmentée. Tout cela est du au changement de l'indice de réfraction entre l'eau et l'air. C.1.2. L’enseignant propose ensuite une activité expérimentale autour de la loi de Descartes afin de la vérifier. Le dispositif expérimental à disposition des élèves est constitué d’une source de lumière émettant un faisceau de lumière de petit diamètre. Ce faisceau passe à travers un hémicylindre de plexiglas et émerge dans l’air. Un rapporteur permet de mesurer les angles d’incidence et de réfraction. C.1.2.1. Donner la définition et la signification de l’indice d’un milieu matériel. L'indice de réfraction d'un milieu matériel est égal au rapport de la vitesse de la lumière dans le vide à la vitesse de la lumière dans le milieu matériel. Les deux vitesses sont exprimées dans la même unité. cet indice est supérieur ou égal à 1. L'indice de réfraction décrit le comportement de la lumière dans un milieu matériel C.1.2.2. Annoter la figure suivante en localisant les deux phénomènes de réfraction mis en évidence. 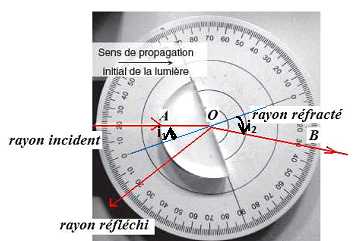En A et en B, le rayon incident est perpendiculaire à la surface séparant les deux milieux : il n'y a pas de déviation. L'angle d'incidence en O est nul, en conséquence l'angle de réfraction est nul. En O, on observe la réfraction du rayon incident à la surface séparant le verre de l'air. Une partie du faisceau incident est réfléchie sur ce dioptre. C.1.2.3. Expliquer pourquoi un seul des deux phénomènes de réfraction permet de vérifier la loi de Descartes pour différents angles d’incidence. Dans la suite, on s’intéresse exclusivement à ce phénomène de réfraction. En A et en B, le rayon incident est perpendiculaire au dioptre, quelle que soit la position du demi-cylindre en plexiglas. Rayon incident et rayon réfracté sont confondus. La loi de Descartes peut être vérifiée en O pour différents angles d'incidence. C.1.2.4. Annoter la figure ci-dessus en faisant apparaître la normale au dioptre, l’angle d’incidence i1 et l’angle de réfraction i2. Voir ci-dessus. 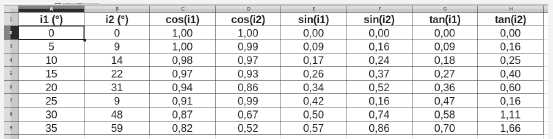C.1.2.5. Les mesures de i1 et de i2 relevées par un binôme d’élèves sont reportées dans un tableur. Ils calculent également le sinus, le cosinus et la tangente de chaque angle. Leur feuille de calcul est donnée. En utilisant ces valeurs, construire une représentation graphique permettant de vérifier la compatibilité des mesures avec la loi de Descartes. Commenter le graphe obtenu et en déduire la valeur de l’indice du plexiglas. définition et la signification de l’indice d’un milieu matériel.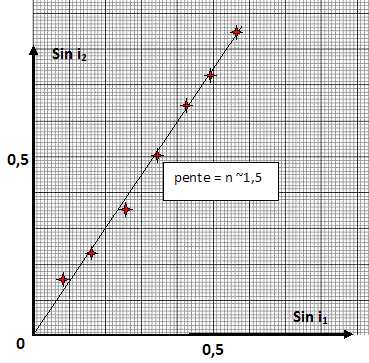 C.1.2.6. Expliciter la raison pour laquelle les élèves n’ont pas réalisé de mesures pour des angles d’incidence supérieurs à 35° ? Citer un dispositif technologique dans lequel ce phénomène est mis à profit. Angle d'incidence limite : sin ilim = 1/n = 1/1,5 =0,667 ; ilim ~42°. Si l'angle d'incidence est supérieur à 42°, il y a réflexion totale. Cela est mis à profit dans la fibre optique pour la transmission d'informations codées en signal lumineux. C.1.3. Dans le cadre des séquences de l’accompagnement personnalisé, il est proposé aux élèves de travailler sur la vision sous l’eau, avec ou sans masque. C.1.3.1. Détailler le défaut optique provoqué par la vision sous l’eau sans masque. Indiquer le défaut de l’oeil humain correspondant. 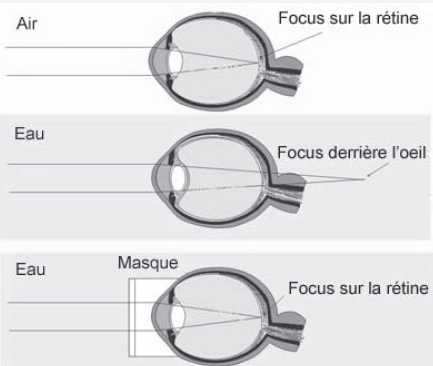Vision sous l’eau sans masque : l'image se forme derrière la rétine, elle est floue. Tout se passe comme si l'oeil n'était pas assez convergent et se comportait comme un oeil hypermérope. C.1.3.2. En utilisant le matériel utile à l’étude des lentilles, proposer une expérience (schéma et protocole) permettant d’illustrer ce défaut optique. Associer le matériel utilisé à la modélisation d’un oeil simplifié. 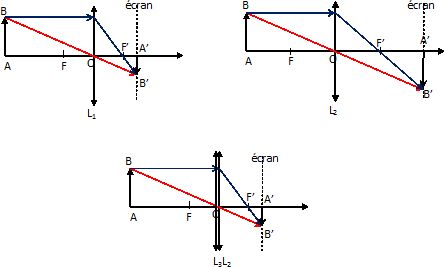Placer sur un banc d'optique un objet lumineux "F" sur la graduation zéro, une lentille convergente L1 de distance focale 10 cm sur la graduation 30 cm et un écran derrière la lentille. Déplacer l'écran afin d'obtenir une image nette de la lettre "F". Cette position servira de repère. L'oeil est assimilable à l'ensemble lentille-écran. Hypermétropie : remplacer la lentille L1 par une lentille L2 de distance focale 15 cm et déplacer l'écran pour retrouver l'image de la lettre "F". Correction de ce défaut : placer une lentille convergente L3 de distance focale 30 cm devant L2. Des ondes à la surface de l’eau. L’enseignant aborde le module SL2 « Comment un son se propage-t-il ? ». Afin de concrétiser la notion d’onde auprès de ses élèves, il exploite l’analogie de comportement entre l’onde sonore et l’onde de surface se propageant le long de la surface libre de la piscine. C.2.1. La photographie suivante présente une portion de la surface libre de l’eau de la piscine, prise de profil. On suppose qu’une onde de surface quasi sinusoïdale se propage. Annoter cette photo en faisant apparaître la longueur d’onde de l’onde associée. C.2.2. Sur un axe gradué en fréquences, placer les domaines correspondant aux infrasons, aux ultrasons, aux sons graves, aux sons aigus et aux sons médiums. Préciser l’ordre de grandeur des fréquences aux frontières des domaines. Les fréquences des médiums sont comprises entre 300 et 1600 Hz. C.2.3. Citer une différence entre les ondes sonores et les ondes se propageant à la surface de l’eau. Les ondes sonores sont longitudinales à trois dimensions. Les ondes à la surface de l'eau sont transversales à deux dimensions. À l’occasion d’une activité expérimentale, l’enseignant propose à ses élèves de mesurer la vitesse des ultrasons dans l’air. Le dispositif expérimental est présenté. L’émetteur d’ultrasons est alimenté par un générateur basse fréquence délivrant un signal sinusoïdal de fréquence f. Deux récepteurs, notés A et B, sont situés respectivement à une distance dA et dB de l’émetteur. Les tensions aux bornes des récepteurs sont visualisées à l’aide d’un oscilloscope (voie 1 pour le récepteur A, voie 2 pour le récepteur B). Les positions des récepteurs sont repérées à l’aide d’une règle graduée. On note xA et xB leurs abscisses. Deux captures d’écran d’oscilloscope réalisées lors de la séance sont présentées. On relève, lors d’une première expérience, xA,1 = 90 mm, xB,1 = 236 mm et puis, lors d’une seconde expérience, xA,2 = 90 mm et xB,2 = 322 mm. Les tensions des voies 1 et 2 de l’oscilloscope sont en phase lorsque le récepteur B est en xB,1. Le récepteur B est déplacé de l’abscisse xB,1 à l’abscisse xB,2 atteinte lorsque les deux tensions sont en phase à nouveau pour la dixième fois consécutive. C.2.4. Proposer une expérience analogue pour les ondes se propageant à la surface de l’eau. Utiliser une cuve à ondes ( vibreur à la fréquence de 10 Hz ) et un stroboscope. C.2.5. En annotant l’une des captures d’écran, déterminer la valeur de la fréquence f des ultrasons. En déduire la célérité c des ultrasons dans l’air. 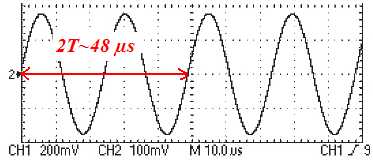T = 2,4 10- 5 s ; f = 1 / T = 4,2 104 Hz. 9 l = xB,2 -xB,1 =322-236 =86 mm ; l = 9,56 mm. c = l f = 9,56 10-3 *4,2 104 = 4,0 102 m/s. En préparant la séance, l’enseignant explore d’autres possibilités offertes par le matériel dont il dispose. L’émetteur d’ultrasons est alimenté par un générateur délivrant une tension périodique correspondant à des « salves ». Cette tension est visualisée sur la voie 1 de l’oscilloscope. La tension aux bornes du récepteur A est visualisée sur la voie 2. Des captures d’écran d’oscilloscope sont présentées. C.2.6. En annotant l’une des captures d’écran , déterminer la distance séparant l’émetteur du récepteur A. 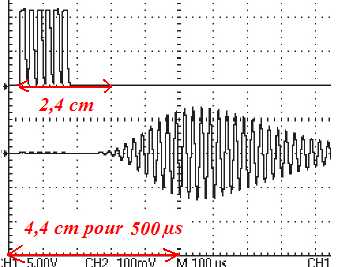Dt = 2,4*500 / 4,4=273 µs. Distance = 4,0 102 *273 10-6 ~0,11 m ~11 cm. C.2.7. En utilisant les propriétés des microphones et des haut-parleurs, expliquer la raison pour laquelle le signal reçu par le récepteur B n’a pas la même forme que le signal alimentant l’émetteur La directivité d'un microphone correspond à sa sensibilité aux sons par rapport à la direction de la source sonore. Lors de la conversions d'un signal sonore en signal électrique, le système microphone  + amplificateur altère le signal audio. Se protéger du bruit. Le maître-nageur sauveteur (MNS) est soumis en moyenne à un niveau acoustique de 85 dB pendant huit heures. On note I0 = 1· 10−12W· m−2 l’intensité acoustique de référence. C.3.1. Calculer l’intensité acoustique moyenne correspondante. En considérant que la surface utile de l’oreille a une aire S = 8· 10−5 m2, calculer la puissance acoustique reçue par l’oreille du maître-nageur. l = I0 10 8,5 = 3,16 10-4 ~3,2 10-4 W m-2. P = I S = 3,16 10-4 *8 10-5 = 2,53 10-8 ~3 10-8 W. Dans le cadre du module HS3, l’enseignant souhaite mettre en place une activité ayant pour thème les protections auditives portées par les MNS en piscine. Au cours de son élaboration, il réalise l’expérience photographiée ci-dessous. L’enseignant obtient ainsi le spectre du son émis par la flûte et perçu au niveau du microphone, en présence ou en l’absence de protection auditive. Ces spectres sont reproduits. C.3.2. Justifier l’utilisation d’une soufflerie dans cette expérience. Dans un instrument à vent, le son est produit par la vibration d'une colonne d'air provoquée par le souffle. C.3.3. Définir la hauteur d’un son, le timbre d’un son et un harmonique. La hauteur d'un son, exprimée en hertz, est la fréquence du mode de vibration fondamentale. En musique, le timbre  des caractères du son, en référence à un instrument donné. Un harmonique est la composante d'un son périodique dont la fréquence est un multiple entier de la fréquence fondamentale. C.3.4. Dans le cadre du module HS3, proposer une exploitation, possible avec les élèves, des spectres obtenus et reproduits ci-dessous. Les cris, facteur principal de fatigue auditive en piscine, sont des sons médium à aigus. 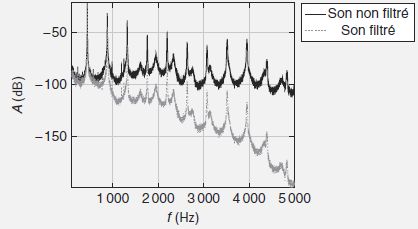Les sons médium sont peu atténués ; les sons aigus sont fortement atténués. C.3.5. L’enseignant souhaite présenter en classe une expérience plus simple montrant l’effet des protections auditives en utilisant un sonomètre. Donner le nom de la grandeur physique qu’il va mesurer. Proposer une expérience possible (un schéma et un protocole succinct sont attendus). Le sonomètre mesure le niveau d'intensité acoustique en décibel. Matériel : sonomètre, GBF, plaques isolantes acoustiques ( divers matériaux ). Mesurer le niveau d'intensité acoustique pour deux fréquences ( 250 Hz et 1000 Hz) avec ou sans plaques isolantes. Conclure : différents matériaux n'ont pas les mêmes qualités d'isolation acoustique et celles-ci dépendent de la fréquence du son. C.4. Glisser sur un toboggan. Dans le cadre de la préparation d’un groupe d’élèves à la poursuite d’études supérieures, le professeur leur propose de réfléchir aux phénomènes physiques mis en jeu dans un toboggan aquatique. C.4.1. On suppose dans un premier temps qu’un enfant glisse sur le toboggan sec. Sa vitesse initiale est nulle. Proposer une modélisation de la situation. Introduire les grandeurs physiques nécessaires sur un schéma. Par un raisonnement clairement explicité, calculer numériquement la valeur de la vitesse maximale que l’enfant pourrait atteindre en bas du toboggan. Un tobogan de plage est constitué par : - une piste DO qui permet à l'enfant partant de D sans vitesse initiale d'atteindre le point O - une piscine de réception : la surface de l'eau se trouve à une distance H au dessous de O. On donne : masse m de l'enfant m = 35 kg ; g = 10 m s-2 ; h = 5,0 m. On choisit le point O comme référence pour l'énergie potentielle de pesanteur. Epp D = m g h. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. Or la vitesse initiale en D est nulle : l'énergie cinétique en D est donc nulle. Par suite : Em D =Epp D= m g h. Or l'énergie potentielle de pesanteur est nulle en O ( référence). Par suite : Em O =Ec O = ½m v20. En absence de frottement, seul le poids travaille et l'énergie mécanique se conserve : Em O = Em D = ½m v20 = mgh. v20 = 2gh ; v0 = [2gh]½. v0 = [2*10*5,0]½ =10 m /s. En réalité la vitesse en ce point n'est que de 5,0 m/s. Les frottements sur le support et sur les couches d'air ne sont pas négligeables et l'énergie mécanique diminue au cours de la glissade sur le tobogan. C.4.2. On suppose dans un second temps que de l’eau coule le long du toboggan mais que personne ne glisse dessus. La vitesse de l’eau est supposée nulle au sommet du toboggan. À l’aide de la relation de Bernoulli, déterminer la valeur de la vitesse de l’eau en bas du toboggan. ½mv12 +mgz1 +p1 = ½mv22 +mgz2 +p2. L'indice 1 corespond au départ ( point D), l'indice 2 à l'arrivée ( point O). p1 = p2 = pression atmosphérique ; v1 = 0. mgz1 = ½mv22 +mgz2 ; g(z1-z2) = ½v22 ; v22 =2gh = 2*10*5,0 = 100 ; v2 = 10 m/s. C.4.3. Proposer une justification à la présence du filet d’eau dans les toboggans aquatiques. L'enfant glisse sans frottement  avec la même vitesse que l'eau. C.4.4. Expliciter les objectifs qui pourraient être poursuivis au cours de la séance d’accompagnement personnalisé. .

menu