Etude
de fonction, équation différentielle.
Bts chimiste 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie A :
La loi de refroidissement de Newton s’énonce ainsi : « la vitesse de
refroidissement d’un corps chaud inerte est proportionnelle à la
différence de température entre ce corps et le milieu ambiant. ». On
appelle T0 la température (en °C) du milieu
ambiant, f (t ) la température (en °C) d’un produit chimique à
l’instant t (en min).
D’après la loi énoncée, f est solution de l’équation différentielle :
(E) : y′ = a(y
−T0).
où y est une fonction de variable t définie et dérivable sur [0 ; +oo[,
y′ sa fonction dérivée et a un
coefficient de proportionnalité non nul.
1.
Résoudre sur [0 ; +oo[ l’équation différentielle (E0)
: y′ −ay
= 0.
y = A exp(-a
t), avec A une constante.
2.
Déterminer un réel c tel que la fonction h constante définie sur [0 ;
+oo[ par h( f ) = c soit une solution particulière de l’équation
différentielle (E).
h' = 0, repport dans E : a(c −T0)
=0 ; c = T0.
3. En déduire la
solution générale de (E).
y
= A exp(-a
t) +T0.
4. Dans une pièce où
la température est T0 = 20 °C, une personne
verse dans un récipient un produit chimique dont la température
initiale est 80 °C.
Montrer que la température du produit à l’instant t vérifie : f (t )
=60 exp(-a t) +20.
y(0) = A exp(0) +20 = 80 ; A =
60 °C.
f (t ) =60 exp(-a t) +20.
5. Sachant que 2
minutes plus tard, le produit est à 60 °C.
a.
Déterminer par le calcul algébrique la valeur exacte de a.
b.
Vérifier que a~
−0,2.
f (2 ) =60 exp(-2a ) +20 = 60 ; .
40 / 60 = exp(-2a )
; 2 /3 = exp(-2a )
;
-2a
= ln(2/3) ; a =0,5
ln 1,5) ~0,2.
|
|
|
Partie B.
On considère la fonction f définie sur [0 ; +oo[ par
f (t )= 60exp(−0,2t) +20.
La représentation graphique C de f dans un repère orthogonal est donnée.
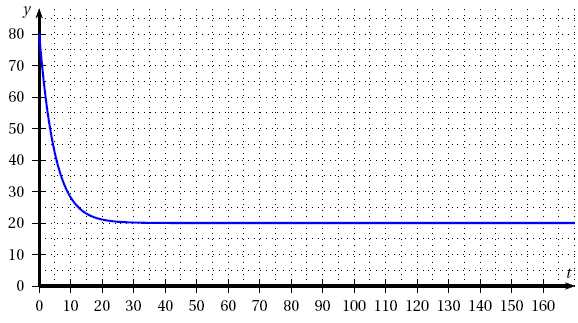
1.
Interpréter l’ordonnée du point de C d’abscisse 0.
80°C est la température initiale.
2. a.
À l’aide du graphique, déterminer la limite de f en +oo.
b. Interpréter ce résultat : à
quoi correspond-il dans le contexte de la partie A ?
La limite de f(t) est 20 lorsque
le temps devient grand.
La température finale du produit est 20°C, température de la pièce.
|
|
|
|
.
3.
Soit g la fonction définie par 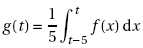
où t est supérieur ou égal à 5.
g désigne la température mesurée par un appareil plongé dans le corps.
a.
Calculer g (t ). En donner une interprétation.
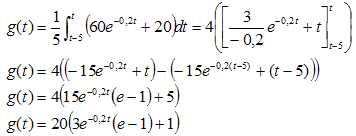
g(t) représente l'aire comprise entre la courbe C, l'axe des abscisses
et les droites d'équation x = 5 et x=t. Cette aire est divisée par 5.
b.
Compléter le tableau de valeurs (on arrondira à 10−1)
fourni, puis tracer la courbe de g sur le graphique donné.
Quelle remarque peut-on faire ?
| t |
5 |
10 |
15 |
20 |
25 |
50 |
100 |
150 |
| g(t) |
57,9 |
33,9 |
25,1 |
21,9 |
20,7 |
20,0 |
20,0 |
20,0 |
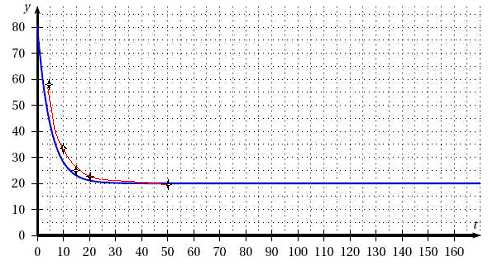
Au bout d'un temps supérieur à 50 minutes, g(t) est constante, égale
àla température de la pièce..
|
|