Lois normale, binomiale, test d'hypothèse. Bts chimiste 2016. . . Partie A : Dans cette partie, les résultats seront donnés arrondis à 10−2. Sur l’ensemble de la production, on prélève de façon aléatoire 500 fioles (prélèvement non exhaustif ) dont les volumes en mL se répartissent dans les 10 classes du tableau suivant : x :entre de  la classe (mL) 11,55 11,65 11,75 11,85 11,95 12,05 12,15 12,25 12,35 12,45 n :effectifs 11 27 53 85 104 97 60 30 18 15 (m-x)2 0,185 0,109 0,053 0,017 0,001 0,005 0,029 0,073 0,137 0,221 n(m-x)2 2,035 2,943 2,809 1,445 0,104 0,485 1,74 2,19 2,47 3,315 1. Donner les valeurs de la moyenne m et de l’écart-type s de cette série. Moyenne m =(11,55 *11 + 11,65 * 27 +11,75 *53 +11,85 *85 +11,95 *104 +12,05 *97 +12,15 *60 +12,25 *30 +12,35 *18 +12,45 *15 ) / 500. m=( 127,05 +314,55 +622,75 +1007,25 +1242,8 +1168,85 +729 +367,5 +222,3 +186,75) / 500 m =11,98 mL. Variance V = (2,035 +2,943 +2,809 +1,445 +0,104 +0,485 +1,74 +2,19 +2,47 +3,315) / 500 =0,039. Ecart type s = V½ =0,039½ =0,197 ~0,20. 2. Soit X la variable aléatoire qui à toute fiole associe son volume en mL.On admet que X suit la loi normale de moyenne 12 et d’écart-type 0,2. a. Calculer la probabilité P(X <=11,8). (11,8-12) /0,2 = -1 ; les tables donnent : 1-P(1) = 1-0,841 =0,159 ~0,16. b. Justifier, éventuellement à l’aide d’un graphique, que pour tout h réel positif, P(12−h <= X <=12+h) = 1−2P(X <=12−h). Donner alors la probabilité P(11,8<= X <=12,2) à partir de celle calculée à la question précédente. 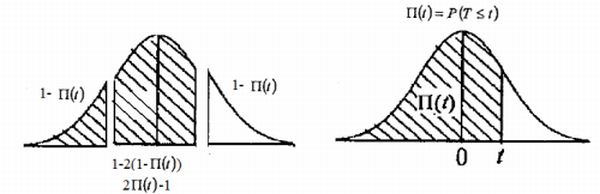P(11,8<= X <=12,2) = 2*0,841 -1 = 0,682 ~0,68. 3. Calculer le nombre h tel que P(12−h <= X <=12+h) = 0,85. 2P(X <=12−h) -1 = 0,85 ; P(X <=12−h) =0,925 ; Les tables donnent : t = 1,44 ; par suit h = t s = 1,44 *0,2 =0,288 ~0,29. Partie B : Un processus de contrôle de la conformité des fioles a été mis au point par l’entreprise. On s’intéresse dans cette partie aux risques d’erreurs de ce contrôle et on suppose que la proportion p de fioles conformes est égale à 0,85. On prélève une fiole au hasard dans l’ensemble de la production. On note : C l’évènement « la fiole prélevée est conforme » ; on a donc P(C) = 0,85. A l’évènement « la fiole prélevée est acceptée par le contrôle ». Une étude préliminaire a permis d’estimer les risques d’erreurs de ce contrôle : - la probabilité de refuser une fiole sachant qu’elle est conforme est 0,05. - la probabilité d’accepter une fiole sachant qu’elle n’est pas conforme est 0,1. Pour les questions suivantes, on pourra faire un arbre de probabilités. 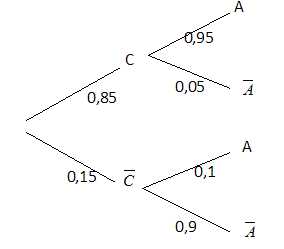1. Déterminer la probabilité qu’une fiole soit acceptée sachant qu’elle est conforme. 0,85*0,95 = 0,8075 ~0,81. 2. Déterminer la probabilité qu’une fiole soit acceptée par le contrôle. 0,85*0,95 +0,15 *0,1 = 0,8225 ~0,82. 3. Déterminer la probabilité qu’une fiole ne soit pas conforme sachant qu’elle a été acceptée par le contrôle. (Arrondir le résultat au millième).  0,15 *0,1 / 0,8225 = 0,0182. . . Partie C. À l’occasion d’une commande, un laboratoire reçoit des fioles de l’entreprise, laquelle lui assure que les fioles ont bien une contenance de 12 mL. Il envisage d’effectuer un test de conformité de la commande reçue, avec la valeur µ = 12 annoncée par l’entreprise. Pour réaliser ce test d’hypothèse bilatéral, il effectuera un prélèvement aléatoire, assimilé à un prélèvement avec remise de 100 fioles prises dans le lot reçu. Soit X la variable aléatoire qui, à un tel prélèvement, associe le volume moyen des 100 fioles. Construction du test. À l’hypothèse nulle H0 : µ = 12, on oppose l’hypothèse alternative H1 : μ différe de 12. Sous l’hypothèse nulle H0, on admet que X suit la loi normale de moyenne 12 et d’écart type s /10 =0,02. 1. En se plaçant sous l’hypothèse H0, déterminer la valeur arrondie à 10−2 du réel h tel que la probabilité P (µ-h <= X <=µ+h) soit égale à 0,95. h = 1,96 s = 1,96 *0,02 =0,0392~0,04. 2. En déduire l’intervalle d’acceptation de l’hypothèse H0 au seuil de risque de 5%. Énoncer alors la règle de décision du test. [ 12-0,04 ; 12 +0,04 ] soit [ 11,96 ; 12,04 ]. Si le volume moyen des fioles appartient à cet intervalle, H0 est vraie, sinon on retient H1. 3. Le laboratoire, après avoir prélevé 100 fioles, constate un volume moyen de 11,79 mL sur cet échantillon. Appliquer le test à l’échantillon puis conclure. 11,79 n'appartient pas à cet intervalle, donc le volume moyen différe de 12 mL. . Partie D. L’entreprise souhaite évaluer le rendement Y , nombre de fioles produites par la machine par minute, en fonction de deux paramètres : T (température de travail du verre donnée en degré Celsius) et P (pression de soufflage du verre donnée en bar). Les niveaux extrêmes pris en compte sont : T (température de travail du verre) : 1 050 °C à 1 200°C P ( pression de soufflage du verre) : 20 bars à 30 bars. X1 est le facteur représentant la température de travail du verre et X2 celui représentant la pression de soufflage du verre. On a : X1 = −1 pour T = 1050 °C et X1 = 1 pour T = 1200 °C X2 = −1 pour P = 20 bars et X2 = 1 pour P = 30 bars. Le plan complet est formé de 4 combinaisons possibles, les résultats sont consignés dans le tableau suivant : Expérience X1 X2 Y N° 1 -1 -1 75 N° 2 1 -1 85 N° 3 -1 1 80 N° 4 1 1 70 On considère que l’expression du modèle est de la forme : Y = a0 +a1X1 +a2X2 +a12X1X2 +e où e est l’erreur commise. 1. Compléter la matrice des expériences et des effets construite selon l’algorithme de Yates; calculer une estimation ponctuelle de chacun des coefficients du  modèle. Expérience Moyenne X1 X2 X1X2 Y N° 1 -1 -1 +1 75 N° 2 +1 -1 -1 85 N° 3 -1 +1 -1 80 N° 4 +1 +1 +1 70 Effet a0 a1 a2 a12 77,5 0 -2,5 -5 Effet global : a0 =(75 +85 +80 +70) / 4 = 77,5. Effet de la température a1 =(85+70) / 2 -77,5 =0,0. Effet de la pression a2 =(80+70) /2 --77,5 =-2,5. a12 = (75+70) / 2 -77,5 = -5. 2. a. Donner l’expression du modèle Y = 77,5 -2,5X2 -5 X1X2 +e. b. À l’aide de ce modèle, quel rendement peut-on prévoir pour une température de 1 100 °C et une pression de 27 bars ? On donnera le résultat arrondi à 10−1. X1 = -1 +  50 *2 / 150 = -0,333 ; X2 = -1 +  7 *2 / 10 = 0,4 ; Y = 77,5 -2,5 *0,4 -5 (-0,333) *0,4 =77,16 ~77,2. . .

menu