Etude de fonction,
équation différentielle.
Bts 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Une
entreprise d’injection plastique est chargée de réaliser par moulage
des hélices de mini-drones dans un nouveau matériau plastique.
La fabrication s’effectue en deux temps :
Phase 1 : injection sous pression de la matière fondue à une
température initiale de 240°C et maintien sous pression de la matière
pendant les 3 premières secondes du refroidissement.
Phase 2 : poursuite du refroidissement et éjection de l’hélice.
À l’issue de ces deux étapes le moule est refermé et une nouvelle
hélice est introduite.
Pour être utilisable, on estime que le matériau plastique ne doit pas
avoir perdu plus de 20% de sa température initiale lors des 3 premières
secondes du refroidissement.
Lors de la fabrication, afin de maîtriser le refroidissement de
l’hélice, on étudie la température T à laquelle le moule doit être
maintenu. En effet, pour garantir un remplissage homogène du moule, le
matériau plastique ne doit pas refroidir trop vite lors de son
injection dans le moule.
Partie I.
Des
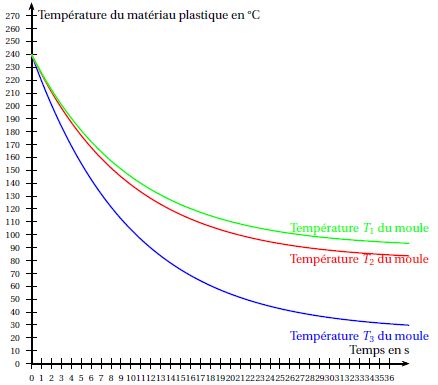
séries de mesures ont permis de réaliser trois courbes de
refroidissement. Elles représentent l’évolution de la température du
matériau plastique (exprimée en degrés Celsius) en fonction du temps
(exprimé en secondes), pour trois valeurs différentes de la température
du moule, T1, T2 et T3.
1. Les trois
températures satisfont-elles aux conditions souhaitées de fabrication
d’une hélice ?
Détailler la réponse.
Le matériau
plastique ne doit pas avoir perdu plus de 20% de sa température
initiale lors des 3 premières secondes du refroidissement.
La température finale du matériau àprès 3 s de refroidissement doit
être supérieure à :
240 *0,8 = 192 °C, ce qui est confirmé graphiquement pour T1
et T2. Par contre T3 ne convient pas.
2.
On estime de plus que le matériau a suffisamment durci et que l’hélice
peut être éjectée sans risque de déformation lorsque sa température
atteint les 100 degrés.
Parmi les températures qui satisfont aux conditions de fabrication,
quelle est la température du moule qui permet de fabriquer le plus
d’hélices dans un temps donné ? Expliquer.
La température de 100°C est atteinte au bout de 22 s pour T2
et au bout de 28 s pour T1.
T2 permet de fabriquer le plus d'hélices en un temps donné.
|
|
|
Partie 2.
On
décide de maintenir le moule à une température de 80°C. On s’intéresse
à la fonction donnant la température du matériau plastique (exprimée en
degrés) en fonction du temps (exprimé en secondes).
On admet que cette fonction est solution de l’équation différentielle
(E) :
(E) : y′+0,1y = 8.
Dans cette équation, y désigne une fonction de la variable réelle t ,
définie et dérivable sur [0 ; +oo[.
1. Déterminer
l’ensemble des solutions de l’équation différentielle
(E0) : y′+0,1y = 0.
y = A exp(-0,1t) avec A une constante.
2. Déterminer le
réel a tel que la fonction g , définie sur [0 ; +oo[ par g (t ) = a
soit une solution particulière de l’équation (E).
g'(t) = 0 , repport dans E :
0+0,1 a = 8 soit a = 80°C.
3. En déduire
l’ensemble des solutions de l’équation différentielle (E).
f(t) = A exp(-0,1 t) +80.
4. Déterminer la
fonction f définie sur [0 ; +oo[, solution de l’équation différentielle
(E) satisfaisant aux conditions de température du problème.
f(0) = 240 = A exp(0) +80.
240 = A +80 soit A = 160.
f(t) = 160 exp(-0,1t) +80.
|
|
|
|
Partie 3.
On considère la fonction f définie sur [0 ; +oo[ par :
f (t )= 80(1+2e−0,1t ).
Cette fonction f donne la température de l’hélice (en degrés) en
fonction du temps t (en secondes) lorsque le moule est maintenu à une
température de 80°C.
1. a. Justifier par
le calcul le sens de variation de la fonction f.
f '(t) = 80 * 2*(-0,1) e−0,1t = -16 e−0,1t
.
Le terme en exponentielle est positif ; f ' (t) est négative et f (t)
est strictement décroissante.
b. Calculer la
limite de f(t) quand t tend vers l'infini.
Le terme en exponentiel tend vers zéro quand t tend vers l'infini ;
f(t) tend vers 80 lorsque t devient grand.
c. Est-il possible
d’interpréter ces résultats dans le contexte du problème ? Si oui,
détailler.
L'hélice atteint la température du moule ( maintenue à 80°C) au bout
d'un temps suffisamment long.
2. a. Résoudre
l’équation f (t )= 100 et donner une valeur approchée par excès à 10−1
de la ou des solutions éventuelles.
100 = 80 (1+2e−0,1t ) ;
1,25 = 1+2e−0,1t ; 0,25 = 2e−0,1t ;
0,125 = e−0,1t ;
ln(0,125) = -0,1 t ; t =20,8 s.
b. Interpréter ce
résultat dans le contexte du problème.
L'hélice dont la température vaut 100°C, peut être éjectée du moule au
bout de 20,8 s.
3. On souhaite de
plus que la température moyenne du matériau plastique, durant la
première phase de fabrication, c’est-à-dire durant les trois premières
secondes, ne soit pas inférieure à 210°C.
On donne ci-dessous une copie d’écran obtenue avec un logiciel de
calcul formel.
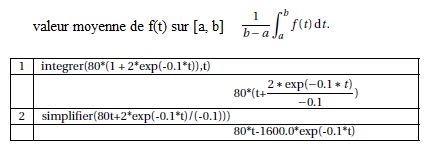
a. En utilisant
cette copie d’écran, calculer la valeur moyenne de f sur l’intervalle
[0 ; 3].
[80 t-1600 exp(-0,1t)]03 / 3 =[80*3-1600
exp(-0,3)] /3 +1600 / 3 =218,2 °C.
b. La fonction f
satisfait-elle la contrainte sur la température moyenne ?
La température moyenne du matériau plastique est voisine de 218°C
durant les trois premières secondes. La contrainte est respectée.
|
|