Etude de fonction, équation différentielle, algorithme.
Bts 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Une société utilise, dans le cadre de son activité de nettoyage de vitres, une nacelle élévatrice
à mât télescopique vertical. On souhaite étudier la durée nécessaire pour que la nacelle
atteigne sa hauteur opérationnelle. On note f (t ) la hauteur, en mètre
de la nacelle à l’instant t , en seconde. On suppose que f une fonction
de la variable t définie et dérivable sur [0 ; +oo[.
A. Résolution d’une équation différentielle.
On considère l’équation différentielle (E) :
y′ +0,3y = 3,6
où y est une fonction inconnue de la variable réelle t , définie et
dérivable sur l’intervalle [0 ; +oo[ et y′ la fonction dérivée de y.
1. Résoudre l’équation différentielle (E0) :
y′ +0,3y = 0.
y= A exp(-0,3t) avec A une constante définie par les conditions initiales.
2. Vérifier que la fonction g , définie sur [0 ; +oo[ par g (t )= 12, est une solution de l’équation différentielle (E).
g'(t) = 0, repport dans (E) : 0+0,3*12= 3,6.
Cette égalité est vérifiée, g(t) = 12 est solution de (E).
3. En déduire l’ensemble des solutions de l’équation différentielle (E).
f(t) = A exp(-0,3 t ) +12.
4. Cette question est une question à choix multiples. Une seule réponse est exacte. On ne demande aucune justification.
On a représenté ci-dessous â l’aide d’un logiciel, certaines solutions de l’équation différentielle (E).
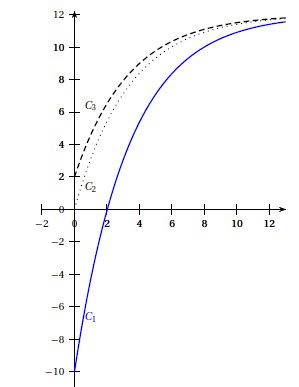
La courbe représentative de la solution f de l’équation différentielle
(E) qui vérifie la condition initiale f (0) = 2 est : la courbe C1, la courbe C2, la courbe C3, au regard de l'oordonnée à 'origine.
|
|
|
B. Étude de fonction et application.
Soit f la fonction définie sur [0 ; +oo[ par f (t ) = −10 exp(−0,3t) +12.
On rappelle que f (t ) désigne la hauteur de la nacelle, exprimée
enmètre, à l’instant t , exprimé en seconde. On désigne par C la courbe
représentative de f dans un repère (O, i, j).
1. Déterminer la hauteur de la nacelle à l’instant t = 0.
f(0) = -10 +12 = 2 m.
2. a. Justifier que la courbe C admet une asymptote dont on donnera une équation.
Quand t temps vers l'infini, le terme en exponentielle tend vers zéro ;
f(t) tend vers 12 quant le temps devient grand. La droite d'équation y
=12 est asymptote.
b. Déterminer le signe de f ′(t ) sur [0 ; +oo[ puis on déduire le sens de variation de la fonction f sur cet intervalle.
f '(t) = -10(-0,3) exp(-0,3t) = 3 exp(-0,3t) ; la dérivée est positive sur cet intervalle.
La fonction f(t) est strictement croissante sur cet intervalle.
c. La vitesse de la
nacelle, en mètre par seconde, à l’instant t , exprimé en seconde, est
modélisée par f ′(t ). Calculer la vitesse de la nacelle à l’instant t
= 0.
f ' (0) = 3 exp(0) = 3 m s-1.
|
|
|
|
Algorithme.
On considère que la nacelle est stabilisée dès lors que sa hauteur f (t ) à l’instant t vérifie l’encadrement :
11,9<= f (t )<=12.
L’objectif de cette partie est de déterminer à partir de quel instant la nacelle peut être considérée comme stabilisée.
1. On considère l’algorithme suivant :
Variable : t est un nombre réel
Initialisation : t prend la valeur 0
Traitement : Tant que f (t ) < 11,9
t prend la valeur t +1
Fin de Tant que
Affichage : Afficher t
Faire tourner cet algorithme « à la main» en complétant le tableau ci-dessous.
Etapes
|
Valeur de t
|
Valeur de f(t)
|
Condition
f(t) <11,9
|
Affichage
|
étape 1
|
0
|
f(0)=2
|
Vraie
|
aucun
|
étape 2
|
1
|
f(1) ~4,59
|
Vraie
|
aucun
|
étape 3
|
2
|
f(2)~6,51
|
Vraie
|
aucun
|
étape 4
|
3
|
f(3) ~7,93
|
Vraie
|
aucun
|
étape 5
|
4
|
f(4) ~8,99
|
Vraie
|
aucune
|
étape 6
|
5
|
f(5)~9,77
|
Vraie
|
aucun
|
étape 7
|
6
|
f(6) ~10,3
|
Vraie
|
aucun
|
étape 8
|
7
|
f(7) ~10,8
|
Vraie
|
aucun
|
étape 9
|
8
|
f(8) ~ 11,1
|
Vraie
|
aucun
|
étape 10
|
9
|
f(9) =11,3
|
Vraie
|
aucun
|
étape 11
|
10
|
f(10) ~ 11,5
|
Vraie
|
aucun
|
étape 12
|
11
|
f(11) ~11,63
|
Vraie
|
aucun
|
étape 13
|
12
|
f(12) ~11,73
|
Vraie
|
aucun
|
étape 14
|
13
|
f(13) ~11,8
|
Vraie
|
aucun
|
étape 15
|
14
|
f(14) ~ 11,85
|
Vraie
|
aucun
|
étape 16
|
15
|
f(15) ~11,89
|
Vraie
|
aucun
|
étape 17
|
16
|
f(16) ~11,92
|
Faux
|
16
|
2. À partir de quel instant t0, arrondi à la seconde, peut-on considérer que la nacelle est stabilisée ?
t0 = 16 s.
3. Proposer une modification de l’algorithme précédent afin qu’il permette d’obtenir une valeur approchée de t0 arrondie au dixième.
Initialisation : t prend la valeur 15
Traitement : Tant que f (t ) < 11,9
t prend la valeur t +0,1.
|
|