Une conduite forcée en travaux. BTs géomètre topographe 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .   A.  Photographie d'un tube. Un géomètre a pris des photographies de la conduite avant travaux. Son appareils est modélisé par deux lentilles minces, permettant d'obtenir l'image nette d'un objet situé à grande distance. L'objectif est constitué de deux lentilles L1 ( f '1 = 250 mm ) et L2 ( f '2 = 5,00 mm). 1. Une image intermédiaire est obtenue par la lentille L1 de centre optique O1. 1.1. Calculer la vergence V1 de cette lentille. Préciser si la lentille est convergente ou divergente en justifiant. V1 = 1 / f '1 = 1 / 0,250 = +4,00 d, valeur positive, la lentille est convergente. 1.2. On considère un objet AB à l'infini. Préciser où se forme son image A1B1 par rapport à la lentille. L'image d'un objet situé à l'infini se trouve dans le plan focal image de la lentille, 25 cm à droite de celle-ci. 1.3. Compléter le schéma suivant. 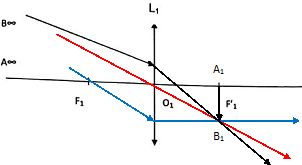2. On utilise ensuite une lentille L2 de centre optique O2 pour permettre une projection de l'image A1B1 sur un capteur situé à une distance constante de L2. 2.1. L2 se trouve à une distance de 10,0 mm après A1B1. Calculer la distance entre les deux lentilles. 250 +10,0 = 260 mm. 2.2. Déterminer par le calcul la position de l'image A'B' de l'objet A1B1 obtenue par L2. 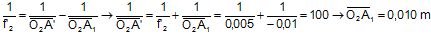2.3. Compléter le schéma suivant. 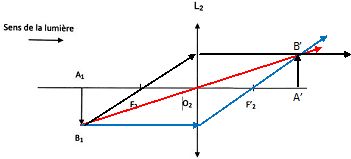On considère maintenant un objet de 2,00 m de haut situé à une distance de 7,00 m avant la lentille L1. 3.1 Calculer la nouvelle position de l'image A1B1 de l'objet AB par rapport à L1. 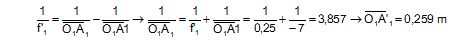3.2. Pour obtenir une image nette sur le capteur, on déplace L1 par rapport à L2. Calculer le nouvel écartement entre les deux lentilles. 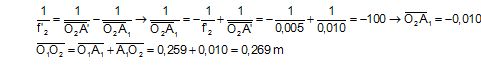3.3. Calculer le grandissement de l'appareil photographique. 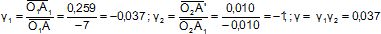3.4.Calculer la taille de l'image A'B'. 2,00 *0,037 = 0,074 m. B. Chute d'une pierre dans une conduite. Les frottements sont négligés. 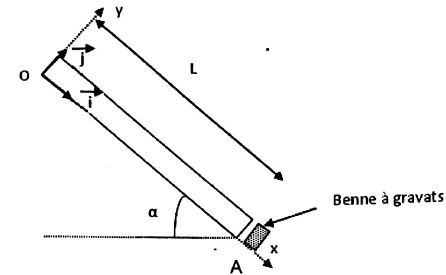L = OA = 9,00 m ; a = 40,0° ; masse de la pierre m = 500 g ; g = 9,81 m s-2. 1. Bilan des forces. 1.1 Faire le bilan des forces extérieures appliquées au centre de gravité de la pierre pendant son mouvement. La pierre est soumise à son poids, verticale, vers le bas, valeur mg = 0,500*9,81 = 4,91 N et à l'action du support, perpendiculaire au support, vers le haut, valeur mg cos a = 4,905 cos40 =3,76 N 1.2 Représenter ces forces sur un schéma. 1.3. Etablir l'expression du vecteur accélération de la pierre et le représenter sans souci d'échelle. 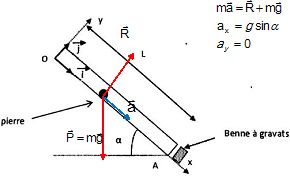1.4. Montrer que les équations horaires du mouvement de la pierre sont :  x(t) = ½g sin at2 ; y(t) = 0. Vitesse initiale et position initiale sont nulles. vx = axt = g sin a t ; vy = 0 ; x(t) = ½g sin at2 ; y(t) = 0. 1.5. Au bout de quelle durée la pierre resortira-t-elle de la conduite ? t = [2L / g sin a)]½ = [18 / (9,81 *sin 40)]½ =1,69 s. 1.6. Quelle sera la vitesse de la pierre en A ? vA = g sin a t = 9,81 *sin 40 *1,69 ~10,7 m s-1. 2. Etude énergétique. 2.1. Enoncer le théorème de l'énergie cinétique. La variation de l'énergie cinétique du système entre les instants t1 et t2 est égale à la somme des travaux des forces extérieures appliquées au système entre ces deux instants. 2.2. Exprimer puis calculer le travail des forces extérieures s'appliquant à la pierre entre O et A. L'action du plan perpendiculaire à la vitesse ne travaille pas. Travail moteur du poids en descente : W = mg OA sin a = 0,500 *9,81 *9,00 *sin 40 ~28,4 J. 2.3. Calculer la variation d'énergie cinétique entre O et A. La vitesse initiale étant nulle, la variation de l'énergie cinétique est égale à ½mv2A = W = 28,4 J 2.4. Calculer vA. vA = [2W / m]½ = [2*28,4 / 0,500]½ =10,7 m /s, valeur identique à celle trouvée ci-dessus. C. Etude de la conduite en fonctionnement. L'eau considérée comme un fluide incompressible parfait, remplit totalement la conduite cylindrique ( de diamètre constant ) du barrage jusqu'à la centrale.       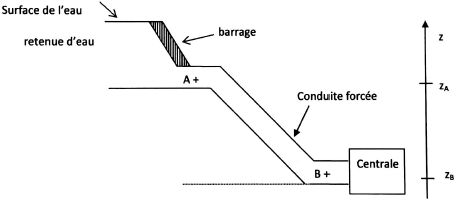1. Etude statique. Une vanne ferme la conduite en bas au point B. 1.1. Calculer la valeur de la pression au point B de la conduite. Pression au point A de la conduite : pA = 15,0 105Pa ; altitudes des points A et B : zA = 1406 m ; zB = 906 m. Masse volumique de l'eau r = 1,00 103 kg m-3. pB -pA = r g (zA-zB)= 1000 *9,81 *500 = 4,91 106 Pa ; pB = 4,91 106 + 15,0 105 =6,40 106 Pa. 1.2. On considère que la pression est constante sur toute la paroi verticale fermant la conduite en B. Calculer la valeur de la force pressante appliquée sur cette paroi. Diamètre de la conduite : D = 1,20 m. Section de la conduite S = pD2 /4 =3,14 *1,22 / 4 = 1,1309 m2. Force pressante F = S pB = 1,1309 *6,405 106 =7,24 106 N. 2. Etude dynamique. La conduite est ouverte et l'eau s'écoule avec un débit massique Qm constant. L'écoulement est considéré comme stationnaire. 2.1. Calculer Qv, le débit volumique. Qm = 11,0 103 kg s-1. Qv = Qm / r = 11,0 103  / 1000 = 11,0 m3 s-1. 2.2 Calculer la vitesse de l'eau dans la conduite. v = Qv / S =11,0 /  1,1309 = 9,73 m s-1.  2.3. Déterminer la valeur de la pression au point B et la comparer avec celle de l'étude statique.. pA + ½rv2A + rgzA =pB + ½rv2B + rgzB. vA=0, la surface de l'eau dans le lac est très supérieure à la section de la conduite ; vB= v. pA + rgzA =pB  ½rv2+ rgzB. pB  = pA + rg(zA -zB) +½rv2. pB  =6,40 106 + 0,5*1000*9,732 = 6,45 106 Pa, valeur supérieure à celle de l'étude statique. .

menu