Lunette, Bernoulli
; grue.
Bts géomètre 2011.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Lunette de
chantier.
Une lunette de chantier est constituée de :
- un objectif, assimilé à une lentille convergente L1 de
distance focale f'1 = 20,0 cm
- une lentille convergente L2 de distance focale f'2=
2,0 cm servant d'oculaire.
L'utilisateur possède un æil normal et on considérera que cet æil
n'accommode pas.
1.1 La lunette
étant afocale, à quelle distance de I'objectif doit-on placer
I'oculaire pour
observer un objet AB situé à I'infini ?
L'image définitive est à l'infini ; l'image intermédiaire, objet pour
l'oculaire, se trouve dans le plan focal objet de l'oculaire. L'image
intermédiaire d'un objet à l'infini se trouve dans le plan focal de
l'objectif. La distance des deux lentilles est égale à f'1+f'2
= 22,0 cm.
1.2 Placer la lentille L2
en utilisant une échelle ½ selon I'axe optique. Construire les images
successives, notées A1B1 et A'B', de I'objet AB
situé à I'infini (A étant sur l'axe optique et AB perpendiculaire à cet
axe).
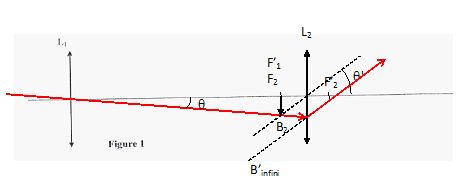
1.3 lndiquer sur
la figure le diamètre apparent q
de I'objet AB et le diamètre apparent q'
de I'image A'B'. Exprimer ces angles considérés comme petits et en
déduire I'expressionet la valeur du grossissement G de la lunette.
tan q = A2B2
/ f'1 ~ q
; tan q' = A2B2
/ f'2 ~ q'.
G =q'
/ q=
f'1 /
f'2
~20 / 2 = 10.
1.4 Le cercle oculaire est I'image
de la monture de I'objectif par l'oculaire. Déterminer par
le calcul sa position et sa taille "d" sachant que I'objectif possède
un diamètre D=5,0 cm.
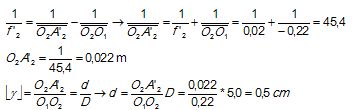 On éloigne L1 de L2
de façon à placer entre ces deux lentilles une troisième lentille
convergente L3.
On éloigne L1 de L2
de façon à placer entre ces deux lentilles une troisième lentille
convergente L3.
L3 est placée à 26,0 cm de l'objectif L1. La
distance focale de cette lentille a pour valeur f'3 = 4,0
cm. On note A1B1 I'image de AB par rapport à L1.
On note A2B2 I'image de A1B1 par rapport à L3.
On note A'B' I'image de A2B2 par rapport à L2.
2.1 Trouver par le
calcul la position de A1B1 par rapport à L3.
A1B1 se trouve
dans le plan focale de L1, l'objet étant à l'infini.
2.2 Trouver par le calcul la
position de A2B2 par rapport à L3.
2.3 A quelle
distance de I'objectif L1 doit-on placer I'oculaire L2
pour que l'æil précédent
puisse voir sans accommoder, l'objet AB situé à I'infini ?
L'oeil n'accommode pas si l'image A'B' se trouve à l'infini. A2B2 est dans le
plan focal objet de L2.
O1O2 = O1O3 +O3A2 +F2O2
=26 +12 +2 =40 cm.
2.4 Construire I'image A1B1
de AB par la lentille L1, l'image A3B3
de A1B1 par L3, l'image A'B' finale.
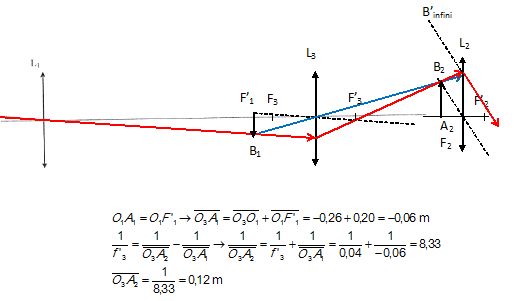
2.5 Quel est
l'intérêt d'ajouter la lentille L3 ?
L'image A'B' est droite par rapport à l'objet.
|
|
|
Ecoulement
de l'eau dans un réservoir en régime permanent.
Accélération de la pesanteur g = 9,8 m.s-2.
Pression atmosphériquet p0 = 1,0 x 105 Pa.
L'eau est considérée comme un fluide parfait (non visqueux) et
incompressible de masse volumique : r= 1,0 x 103 kg.m-3.
La relation de Bernoulli peut s'écrire, en notant z la cote d'un point
sur un axe vertical orienté vers le haut : p + r v2/2 + rgz =constante.
Un réservoir cylindrique d'axe vertical de rayon R = 100 m et contenant
une hauteur d'eau H = 2,5 m est relié à une canalisation cylindrique de
rayon a = 20 cm. ll y a une dénivellation h = 5,0 m entre la prise
d'eau B du réservoir et la sortie C de la canalisation
En régime d'écoulement permanent la sortie C de la canalisation
est à l'air libre et la hauteur H sera considéré comme pratiquement
constante. Le niveau de référence (z = 0) est le niveau de fond du
réservoir. On veut calculer, en régime permanent, la vitesse
d'écoulement vC de I'eau à la sortie de la canalisation.
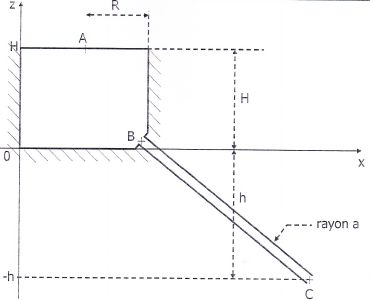
1. Que
peut-on dire du débit volumique qv à l'entrée B et à la
sortie C de la canalisation ?
En déduire une relation entre la vitesse de l'eau vB en B et
la vitesse de l'eau vc en C.
Le débit volumique reste constant ; le diamètre de la canalisation
étant constant, la vitesse de l'eau en B est égale à la vitesse de
l'eau en C. vB =vc.
2. Ecrire la relation liant les
pressions pB et pC. Simplifier cette relation en
utilisant la
question 1 et donner une expression de pB.
pB + r vB2/2
+ rgzB
=pC + r vC2/2
+ rgzC
;
pB
+ rgzB
=pC +
rgzC
;
pC - pB
= rgzC
- rgzB
= rgzC ; pB - pC =rgh.
3. Écrire la relation liant les
pressions pA en A et pB en B. Justifier le fait
que l'on puisse
négliger la vitesse du fluide vA dans le réservoir.
Simplifier alors la relation précédente et
donner une expression de pB.
pB
+ r vB2/2
+ rgzB
=pA + r vA2/2
+ rgzA.
La surface du réservoir étant très grande devant le diamètre de la
canalisation, vA est
proche de zéro. De plus pA = p0 et zB=0.
pB + r vB2/2
=p0 +
rgH.
pB
-p0
= rgH -r vB2/2.
4. Montrer que la vitesse
d'écoulement peut s'écrire : v =[2g(H+h)]½.
Calculer numériquement cette vitesse.
pC = p0, l'eau en C se trouve à l'air libre.
p0
- pB =rgh
et pB -p0
= rgH -r vB2/2.
-rgh= rgH -r vB2/2
;
vB2/2
= gH+gh ; v =[2g(H+h)]½
= [2*9,8 *7,5 ]½ =12,12 ~12 m /s.
5. Calculer le débit volumique Qv
de l'eau dans la canalisation.
Qv
= v p a2
= 12,12 *3,14 *0,22 = 1,53 ~1,5 m3 s-1.
6. Calculer le débit massique Qm
de l'eau dans la canalisation.
Qm
= r Qv =1,5 103
kg s-1.
|
|
|
|
Oscillations
de la charge d'une grue.
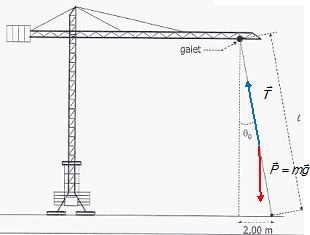
Une grue soulève une charge, assimilée à un point matériel, de masse m
= 1500 kg à l'aide d'un câble d'attache de longueur l = 30 m de masse
négligeable par rapport à m. On donne I'accélération de la pesanteur: g
= 9.8 m.s-2.
Dans toute la suite du problème, on négligera toutes les forces de
frottements et on notera q
I'angle que fait le câble avec la verticale.
1. A I'instant ou
la charge décolle du sol, elle est décalée de 2 mètres par rapport à la
verticale passant par le galet de la grue .
Calculer l'angle q0
que fait le câble avec la verticale à cet instant.
tan q0
= 2 / L = 2 / 30
=0,0667 ; q0 = 3,81 ~3,8 °.
2. Préciser le
référentiel d'étude.
Référentiel terrestre supposé galiléen.
3. Faire le bilan
des forces s'exerçant sur la charge, à un instant t quelconque après le
début du mouvement. Les représenter sur un schéma.
La charge est soumise à son poids et à la tension du câble.
4. Ën appliquant le
théorème de l'énergie cinétique, exprimer puis calculer la vitesse
linéaire v avec laquelle la charge passe à la verticale du galet de la
grue.
La charge oscille entre les positions q0 et -q0. Le travail de la
tension est nul, celle-ci étant à chaque instant perpendiculaire à la
vitesse.
Travail moteur du poids entre les positions q0 et 0 : W =mg l(1-cosq0)
Variation
de l'énergie cinétique : ½mv2 -0 = ½mv2.
Théorème de l'énergie cinétique : ½mv2 = mg l(1-cosq0).
v = [2g l(1-cosq0)]½ =[2*9,8 *30(1-cos 3,8)]½
=1,14 ~1,1 m/s.
5. L'application du théorème du
moment cinétique conduit à l'équation différentielle suivante:
q" +g
/ l sin q = 0.
5.1 Dans
l'approximation des oscillations de faible amplitude, montrer que I'on
a un oscillateur harmonique.
sin q ~q et q" +g / l q = 0.
5.2 Donner
I'expression de la période des petites oscillations et calculer sa
valeur.
w = [g
/ l ]½ ;
T = 2p / w = 2p [ l /g]½ =
2*3,14 [ 30 /9,8]½ ~ 11 s.
|
|