Le thé japonais et
la radioactivité, viscosité d'un lait.
BTS Bioanalyses et controles 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
A. Le thé japonais et la radioactivité.
15 juin 2011 : un
thé provient du Sud-ouest de Tokyo, ville touchée par la catastrophe
nucléaire de Fukushima. les feuilles de thé ayant capté des quantités
importantes de Césium 137, ce lot de thé est radioactif. Après infusion
des feuilles contaminées dans un litre d'eau chaude, on détecte une
activité radioactive de 40 Bq..
1.
Donner la composition du noyau de césium 13755Cs.
55 protons et 137-55 = 82 neutrons.
2. Le césium 137 est un isotope du
césium 134. Donner la signification du terme isotope.
Des isotopes ne diffèrent que par leur nombre de neutrons. Ils ont le
même numéro atomique.
3. Le césium 137
est radioactif ß-. L'équation de désintégration du césium
137 est de la forme :
13755Cs
---> AZX + 0-1e.
Déterminer les valeurs de A et Z, identifier X en précisant les lois
utilisées.
Conservation de la charge : 55 = Z-1, d'où Z = 56 ; on identifie le
baryum Ba.
Conservation du nombre de nucléons : 137 = A +0, d'où A = 137.
4.
L'activité d'un kilogramme de ce thé a été mesurée à 1000 Bq, ce
qui est supérieur à la norme autorisée.
4.1.
Indiquer ce que représente une activité de 1 Bq.
1 Bq correspond à une désintégration radioactive par seconde.
4.2. Définir la
demi-vie radioactive t½.
La demi-vie
radioactive est la durée au bout de laquelle l'activité initiale a été
divisée par deux.
4.3.
Si ce kilogramme de thé radioactif n'avait pas été détruit, son
activité aurait atteint la norme autorisée en 2041. En déduire la
valeur de l'activité correspondant à cette norme autorisée.
Demi-vie du Césium 137 : t½ = 30 ans.
A = A0 exp (-l
t) ; l = ln
2 / t½ = ln2 / 30 = 0,0231 an-1.
2041-2011 =30 ans.
A = 1000 exp(-0,0231 *30) =500 Bq par kg de thé..
5.
Le sievert ( Sv) est une unité qui permet d'évaluer les effets
biologiques des rayonnements sur le corps humain. Le millisievert est
couramment amployé pour exprimer la dose efficace D reçue par une
personne exposée à la radioactivité. Dans le cas d'une ingestion d'un
aliment contaminé, la conversion de l'activité A de l'aliment en dose
efficace D est donnée par la relation :
D = F A où F est un facteur de dose par ingestion ( en mSv par Bq).
Pour le Césium 137, F = 1,4 10-5 mSv Bq-1.
5.1. Déterminer la
dose efficace D reçue par un consommateur buvant un litre de thé
radioactif d'activité A = 40 Bq, durant une journée.
D = 40 *1,4 10-5 = 5,6 10-4 mSv.
5.2. En considérant
l'activité constante sur une année, montrer que le sonsommateur reçoit
une dose efficace proche de 0,20mSv par an.
5,6 10-4 *365 ~0,20 mSv an-1.
5.3.
Les sources d'exposition aux rayonnements radioactifs naturels ou
artificiels sont multiples. Par exemple, la dose reçue peut atteindre
0,30 mSv lors d'une radiographie des poumons. Dans ces conditions, la
seule consommation du thé contaminé
mettrait-elle la santé des consommateurs en danger
?
Il n'y a pas de mise ne danger, la dose efficace due au thé est
inférieure à celle reçue lors d'une radio des poumons.
|
|
|
B. Viscosité d'un lait de vache.
Plus
la viscosité d'un liquide est élevée, plus celui-ci s'écoule
difficillement. Dans le cas du lait, les teneurs en protéines et en
matière grasse influent de façon importante sur la viscosité.
Lors d'une recherche, une étudiante a trouvé pour un lait de vache une
viscosité double de celle de l'eau. Elle souhaite valider ou infirmer
cette information.
Pour cela, elle utilise un viscosimètre à chute de bille qui comporte
un long tube de verre vertical, remplit de lait écrémé et dans lequel
elle laisse tomber une bille sphérique. Le mouvement vertical
descendant est uniforme entre deux repères X1 et X2.
L'étudiante mesure la durée moyenne Dt nécesaire au déplacement de la
bille entre ces deux repères séparés d'une distance d = 30,0 cm.
1. La durée moyenne Dt vaut 15,8 s. Montrer que la vitesse moyenne de la bille est v = 1,90 10-2 m/s.
v = d / Dt = 0,30 / 15,8 = 1,90 10-2 m /s.
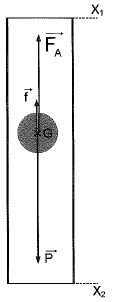
Les forces appliquées à la bille lors de sa chute rectiligne et uniforme, sont représentées ci-dessous.
Poids : P = mg ; poussée d'Archimède F = rLVg avec rL : masse volumique du lait en kg m-3 et V volume de la bille ( m3).
Force de frottement fluide f = 6 p r hL v.
|
|
|
|
2.
En appliquant le principe d'inertie au mouvement de la bille, on montre
que P = f +F. En déduire que la viscosité du lait est donné par la
relation : hL = (P-F) / (6p r v).
P -f = f = 6 p r hL v , par suite : hL = (P-F) / (6p r v).
3. Pour déterminer la viscosité du lait, il est nécessaire de connaître le poids de la bille.
Rayon de la bille r = 1,00 mm ; masse volumique de la bille rB =1050 kg m-3.
3.1. Calculer la masse de la bille.
Volume de la bille V = 4 / 3 p r3 = 4 / 3 *3,14 *(10-3)3 =4,189 10-9 m3.
masse de la bille m = rB V =1050 *4,189 10-9 ~ 4,4 10-6 kg.
3.2. Montrer que le poids de la bille a pour valeur P = 4,31 10-5 N.
P = mg = 4,4 10-6*9,81 = 4,31 10-5 N.
4. L'étudiante a déterminé la masse volumique du lait afin de calculer la poussée d'Archimède. Elle aboutit à F = 4,24 10-5 N.
4.2. Proposer un protocole pour déterminer expérimentalement la masse volumique du lait.
Mesurer un volume précis de lait ; peser ce volume : rL = m / V avec m en kg et V en m3.
4.2. Calculer la viscosité du lait.
hL = (P-F) / (6p r v) = (4,31-4,24) 10-5 / (6*3,14*10-3 *1,90 10-2)=1,95 10-3 Pa s.
5. L'étudiante peut-elle valider ou invalider l'information trouvée sur internet ?
La viscosité de l'eau est égale à 1,00 10-3 Pa s.
La viscosité trouvée pour ce lait est voisine du double de la viscosité de l'eau.
L'information est validée.
|
|