Combustion
du propane, Bernoulli, principe d'un manostat. Bts agro-équipement 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Consommation d'un
chauffe-eau.
On considère le fonctionnement d'un chauffe-eau durant une minute. Ce
chauffe-eau utilise du propane C3H8
comme combustible. Il permet sur cette durée, de porter à la
température qf
=60 °C un volume V =3,0 L d'eau de température initiale qi
= 15°C.
1.
Montrer que l'énergie thermique Q reçue par les 3 L d'eau vaut 564 kJ.
Q = meau ceau (qf -qi ) =3,0 *4180 (60-15) =5,64 105
J = 564 kJ.
2.
La combustion du propane pour chauffer ces 3 L d'eau a libérée une
énergie E = 806 kJ. Calculer le rendement de ce système.
Energie utile / énergie consommée =564 / 806 ~ 0,70 ( 70 %).
3.
Le pouvoir calorifique du propane est Pc = 4,6 104
kJ kg-1. Calculer la masse de propane nécessaire.
m =E / Pc
= 806 / (4,6 104) =0,0175 kg = 17,5 g.
4. Montrer que la quantité de
matière correspondante vaut n = 0,40 mol environ.
M(propane) = 3*12+8 = 44 g/mol ; n = m /M(propane) = 17,5 /44
=0,398 ~0,40 mol.
5. Ecrire l'équation
de la combustion complète du propane.
C3H8(g) +5O2(g)
= 3 CO2(g) + 4H2O(g).
6. Calculer le
volume de dioxygène nécessaire. Vm = 24 L mol-1.
n(O2) = 5 n = 5*0,40 ~ 2,0 mol.
V(O2) = n(O2) Vm
=2,0 *24 = 48 L.
7.
Quel réactif de cette réaction doit être en excès pour assurer une
combustion complète ? Comment peut-on s'en assurer ?
Le dioxygène doit être en excès pour que la combustion du
propane soit complète. On n'observe pas de dépôt noir de carbone, pas
de formation de monoxyde de carbone CO. La flamme est bleue et non pas
rouge.
Réservoir
de stockage d'eaux de lavage.
Le réservoir de stockage présente des dimensions très grandes par
rapport à celles de l'orifice d'évacuation situé à une profondeur L =
1,20 m au dessous de la surface libre du liquide. La vidange s'effectue
plus rapidement grâce à l'augmentation de la pression de l'air au
dessus de la surface libre du liquide jusqu'à la valeur p1
= p0 +p, où p0 représente
la pression atmosphérique et p = 7,0 103 Pa.
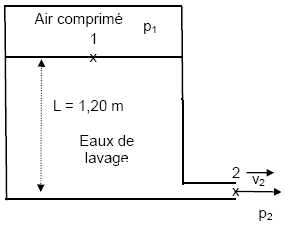
1.
Que vaut la pression p2 du liquide au niveau
del'orifice d'évacuation placé à l'air libre ?
p2 = p0, liquide en
contact avec l'air libre.
2.
La vitesse v1 d'écoulement en haut du réservoir
est considérée comme nulle. Calculer v2 si le
liquide a une masse volumique égale à celle de l'eau.
Equation de Bernoulli : ½(v22-v12)
+(p2-p1) / r +g(z2-z1)=0.
0,5 v22 -p / r
-gL = 0 ; v2
=(2(p
/ r +gL))½ =(7 103
/ 1000 +9,8 *1,2)½ =6,125 ~6,2 m /s.
3.
Dans certains cas, les eaux de lavage peuvent contenir des produits
organiques ; la masse volumique du liquide est alors inférieure à celle
de l'eau. Comment est modifiée v2 ?
Le terme p / r augmente, la vitesse v2
croît.
4.
Comment évolue v2 au cours de la vidange si p1
est constante.
Le terme gL diminue, v2 décroît.
|
|
|
Principe
d'un manostat pour compresseur.
Ce dispositif permet de couper l'alimentation du compresseur lorsque la pression de gonflage désirée est atteinte.
Etude du bloc n°1.
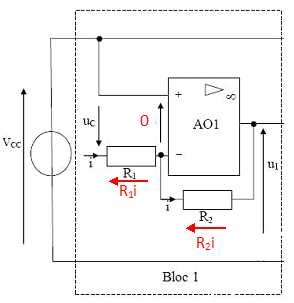
L'amplificateur fonctionne en régime linéaire. R1 = 1 kW ; R2 = 100 kW. Vcc = 12 V.
1.1. Ecrire les relations entre i, uc et R1 et entre Vcc, R2, i et u1.
uc = R1 i ; Vcc =u1+R2i.
1. 2. En déduire que u1 = Vcc-R2 / R1 uc.
i = uc / R1 ; Vcc =u1+R2 / R1 uc ; u1 = Vcc-R2 / R1 uc.
1.3. A l'aide de la caractéristique du capteur de pression, préciser les valeurs minimale uc min et maximale uc max de la tension uc délivrée par le capteur de pression.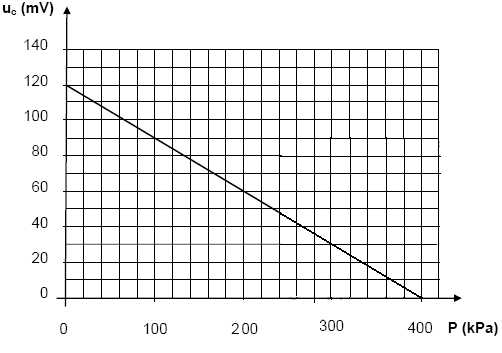
uc min = 0 ; uc max =0,12 V.
1.4. En déduire les valeurs minimale u1 min et maximale u2c max de la tension u1.
u1 min=12-100*0,12 = 0 V ; u1 max=12-100*0 = 12 V.
|
|
|
|
Etude du bloc 2.
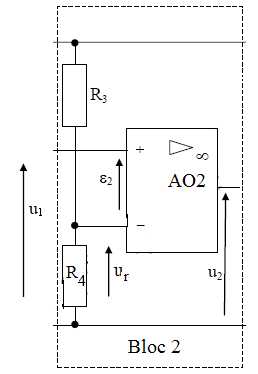
R3 = 860 ohms ; R4 variable de 0 à 3,3 kW.
2.1. Quel est le régime de fonctionnement de l'AO2 ? Justifier.
Mode saturé : il n'y a pas de liaison entre l'entrée inverseuse et la sortie.
2.2. Exprimer ur en fonction de R3, R4 et Vcc. En déduire que ur = 3,6 V quand R4 =370 W.
ur = R4 i' ; Vcc =(R3+R4) i' = (R3+R4) /R4 ur ; ur = R4 / (R3+R4) Vcc.
ur = 370 /(860+370) *12 =3,6 V.
2.3. Donner l'expression de e2 en fonction de u1 et ur.
e2 = u1-ur.
2.4. Quelle est la valeur de la tension u1 qui provoque la commutation de la tension u2 ?
Si u1 > ur, u2 = Vh = +12 V ; Si u1 < ur, u2 = Vb = 0 V ; u1 =3,6 V provoque la commutation.
2.5. En déduire la valeur de la tension uc correspondante. Déterminer la pression P correspondante, appelée pression de consigne.
u1 = Vcc-R2 / R1 uc = 12-100 uc ; uc =(12-u1) /100 = (12-3,6) /100 = 0,084 V = 84 mV.
Le graphe ci-dessus donne P = 120 kPa.
Synthèse.
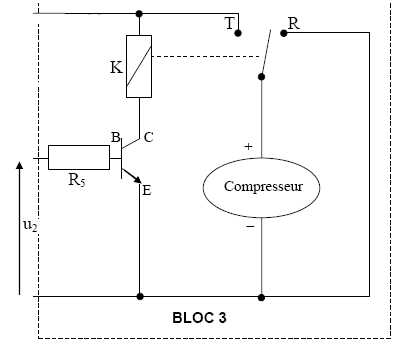
K est un relais ( 12 V , 1020 mA). Il assure le contact travail ( position T), quand sa bobine nest pas alimentée. R5 = 820 ohms.
3.1. Quel composant du montage permet le réglage de la pression de consigne ?
R4 variable de 0 à 3,3 kW.
3.2. Supposons
que la pression p dans le réservoir soit inférieure à la pression de
consigne P désirée, montrer alors que le compresseur est bien alimenté.
p est inférieure = 120 kPa, uc est supérieure à 0,084 V.
u1 = 12-100 uc devient inférieure à 3,6 V et u1 < ur, u2 = Vb = 0 V.
Le transistor, qui fonctionne en commutation, est bloqué : VCE = 12 V.
La bobine du relais est alimenté et assure le contact R, mise en route du compresseur.
|
|