Détection et
habitabilité d'une exoplanète. Bac S Amérique du nord 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Cet exercice aborde certains aspects du principe de détection d'une exoplanète et envisage sa possible habitabilité.
Principe de détection par vélocimétrie basée sur l'effet Doppler. Une
exoplanète tourne autour d'une étoile autre que le soleil. L'ensemble
des deux est appelé système {étoile-planète}. Le principe de la méthode
s'appuie sur l'étude de la trajectoire de l'étoile autour d'un point G appelé centre de symétrie du système {étoile-planète}. La
planète et l'étoile sont en mouvement de rotation autour du centre de
gravité G. On enregistre les spectres de raies de l'étoile sur des
cycles de plusieurs nuits, ce qui permetde mettre en évidence des
oscillations périodiques de la longueur d'onde des raies observées. Ces
oscillations peuvent être reliées, grâce à l'effet Doppler, au
mouvement de rotation de l'étoile autour du centre de gravité G du
système. La vitesse radiale de l'étoile ( vitesse suivant l'axe
d'observation terre-étoile ) peut alors être déterminée par cette
étude. Elle est composée d'une vitesse moyene ( vitesse du système par
rapport à l'observateur terrestre ) à laquelle s'ajoute une
perturbation qui varie périodiquement. La période de la perturbation
donne la période du mouvement de l'étoile qui est aussi la période du
mouvement de la planète. D'après
http://culturesciencesphysique.ens-lyon.fr. La méthode des vitesses
radiales utilisée permet de distinguer assez facilement les orbites
circulaires des orbites elliptiques. Les planètes en orbite circulaire
correspondent à des étoiles dont les variations de vitesse radiale sont
régulières et symétriques en forme de sinusoïde ( graphe de gauche ).
Lorsque la trajectoire est une ellipse allongée, il apparaît des pics
dans lacourbe de vitesses ( graphe de droite ). 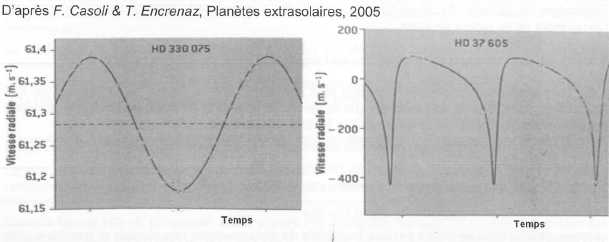 Le système HD 189733. Les
caractéristiques de l'étoile sont assez proches de celle du soleil :
températures de surface voisines, la masse de l'étoile est M = 0,82 M 0, où M 0 est la masse du soleil ( M 0 = 1,989 10 30 kg). Variation des vitesses radiales de cette étoile. 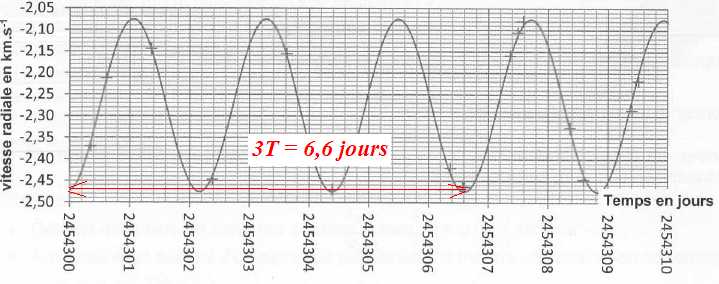
|
|
|
1.1.
Le décalage spectral est lié au mouvement de rotation de l'étoile
autour du centre de gravité G. On rappelle que le décalage spectral Dl = l -lmesurée, où l est une longueur d'onde de référence et lmesurée sa valeur perçue depuis la terre, permet de déterminer la vitesse v de déplacement du système par la relation : Dl / l = v / c. l = 656,2 nm ; c : célérité de la lumière dans le vide.
Quelles mesures, réalisées par l'observatoire de Hte Provence, ont permis de tracer la courbe ci-dessus. ? Expliquer la démarche des chercheurs.
Le
mouvement de la planète provoque en effet un léger déplacement des
raies d'absorption du spectre de l'étoile par effet Doppler. La
longueur d'onde de certaines raies d'absorption spectrales augmente et
diminue de façon régulière sur un intervalle de temps donné.
A
intervalle de temps réguliers, les chercheurs réalisent le spectre de
raies de l'étoile et isolent dans ce dernier la raie correspondant à la
longueur d'onde de référence ; ils déterminent la vitesse radiale
à partir de la relation ci-dessus.
1.2. Déterminer la période de révolution de cette étoile ainsi que celle de l'exoplanète de ce même système.
La période de la perturbation donne la période du mouvement de l'étoile qui est aussi la période du mouvement de la planète. T = 2,2 jours.
1. 3. Quelle est la nature de la trajectoire de l'exoplanète autour de son centre de gravité G ?
Les planètes en orbite circulaire correspondent à
des étoiles dont les variations de vitesse radiale sont régulières et
symétriques en forme de sinusoïde.
1.4.
La masse de l'étoile étant beaucoup plus importante que la masse de la
planète, on fera l'hypothèse dans la suite de l'exercice que le centre
de gravité G du système peut être confondu avec le centre de l'étoile,
les résultats établis restent valables. Montrer que le mouvement de
l'exoplanète de ce système est nécessairement uniforme.
Référentiel étoilo-centrique.
La
planète est soumise uniquement à la force de gravitation exercée par
l'étoile, celle ci est centripète, dirigée vers le centre de l'étoile.
La vitesse de l'exoplanète est portée, à chaque instant par la tangente
à l'orbite circulaire.
Une force perpendiculaire à la vitesse ne
travaille pas. L'énergie cinétique de l'exoplanète, et en conséquence
la valeur de sa vitesse, restent constantes. Le mouveent de
l'exoplanète est donc uniforme.
|
|
|
|
2. Habitabilité de cette exoplanète.
La
zone d'habitabilité se définit par une fourchette de distance
entre une planète et son étoile. Elle correspond à une zone dans
laquelle la quantité d'énergie reçue par la planète permet à l'eau
d'exister sous forme liquide. ( cas de la terre située à 1 U.A
qui reçoit environ 1000 W par m2 d'énergie rayonnée par le
soleil ). Si on s'approche du soleil et que l'on dépasse Vénus, située
à 0,723 U A, la quantité d'énergie est trop importante et l'eau
se vaporise. Si on s'éloigne et que l'on dépasse Mars située à 1,52 U
A, alors l'eau n'existe que sous frme de glace. Or seule l'eau liquide
permet à la vie d'exister sous la forme que nous lui connaissons. 1U A
= 1,50 108 km.
La taille et la position de la zone
d'habitabilité dépend naturellement de la puissance de l'étoile
qui émet le rayonnement lumineux. Sil'étoile est petite, la zone
d'habitabilité sera beaucoup plus proche d'elle que s'l sagit d'une
étoile géante.
D'après http://sciencesavenir.fr.
On se propose de déterminer la distance séparant l'étoile de son exoplanète.
2 .1 Enoncer la troisième loi de Kepler.
Le carré de la période de révolution T est proportionnel au cube du rayon r de l'orbite de l'exoplanète.
T2 = k r3 avec k une constante.
2 .2 Montrer,
en utilisant la deuxième loi de newton et en explicitant les différents
termes, que pour une trajectoire circulaire cette loi s'écrit :
T2 / r3 = 4p2 /(GM) avec M masse de l'étoile centrale.
L'exoplanète décrit la circonférence 2 p r à la vitesse v durant la période T : 2 p r = v T ;
d'une part v2 = GM/r ; d'autre part : v = 2 p r/ T soit : v2 = 4 p2 r2 / T2.
Par suite : GM / r = 4 p2 r2 / T2 ou T2/r3 = 4p2 / (GM).
2 .3 En déduire la distance moyenne entre la planète et l'étoile.
r3 = T2GM / (4p2) =(2,2 *24*3600)2 *6,67 10-11 *0,82*1,989 1030 / (4*3,142)=9,96 1028.
r = 4,63 109 m ou 4,63 109 /(1,50 1011 )=0,031 U A..
2 .4 Cette exoplanète appartient-elle à la zone d'habitabilité ?
Non, 0,031 < 0,723, elle est trop proche de son étoile.
|
|