L'orgue marin de
Blackpool. Bac S Amérique du Sud 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
L’orgue
marin de Blackpool (station balnéaire située au nord de Manchester en
Angleterre) est une sculpture musicale de 15,0 mètres de haut,
construite en 2002, et dont l’auteur a voulu qu’elle soit une «
manifestation musicale de la mer ».
La houle à marée haute pousse l’air dans des tuyaux placés dans la
digue face à la mer, ce qui fait alors sonner dix-huit tuyaux d’orgue
ouverts aux deux extrémités. Les longueurs des tuyaux d’orgue sont
choisies pour jouer une série harmonique en si bémol. Sur le panneau
explicatif placé au pied de la structure, on peut lire : « La note
jouée la plus basse est un si bémol (notée Si b) ; la hauteur de la
deuxième note jouée est le double de celle de la première, la hauteur
de la troisième est le triple de la hauteur de la première et ainsi de
suite… »
Question préliminaire :
Parmi les trois tuyaux représentés sur le plan à l’échelle de
l’orgue, indiquer celui qui joue la note la plus grave. Justifier.
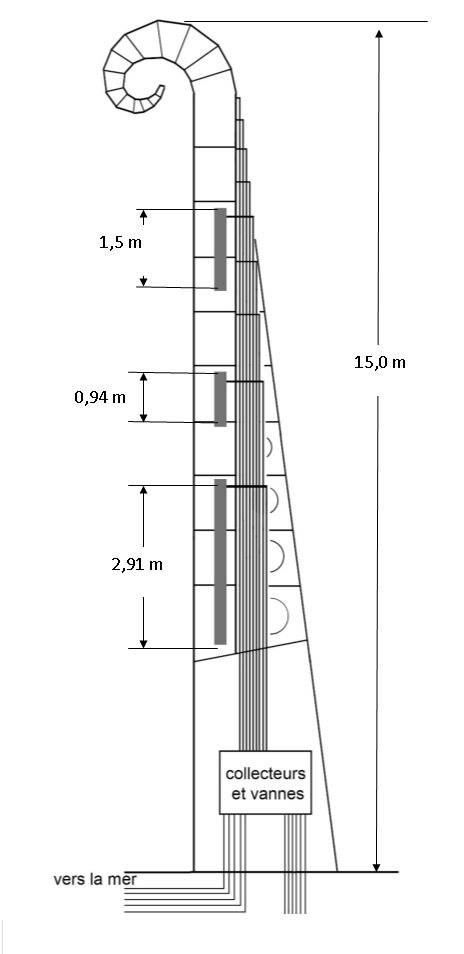
Seuls les trois plus grands tuyaux d’orgue sur les dix-huit au total sont représentés sur le schéma.
|
|
|
Fréquence fondamentale d’un tuyau d’orgue
Pour un tuyau d’orgue ouvert aux deux extrémités, la longueur L (en m)
du tuyau et la fréquence f (en Hz) du son émis sont liées par la
relation :
L = vson / (2f).
Les sons les plus graves ont les
fréquences les plus faibles, ce qui correspond au tuyau d'orgue ayant
la plus grande longueur ( 2,91 m).
|
|
|
|
Problème
: à l’aide des informations données par les différents documents,
vérifier la phrase inscrite sur le panneau explicatif (en gras dans le
texte introductif). Cette phrase est-elle vraie tout au long de l’année
? Justifier.
Fréquence de la note jouée la plus basse : fmini = vson / (2Lmax) avec Lmax = 2,94 m.
Vitesse du son dans l'air en hiver ( température moyenne 4 °C) :
vson = 331,5 +0,607 x 4 = 333,9 m /s.
fmini = 333,9 / (2x2,91) = 57,4 Hz.
La note est un peu inférieure au Si b, octave 0.
Vitesse du son dans l'air en été ( température moyenne 15 °C) :
vson = 331,5 +0,607 x 15 = 340,6 m /s.
fmini = 340,6 / (2x2,91) = 58,5 Hz.
La note se rapproche du Si b, octave 0 ( 58,3 Hz).
Fréquence de la note suivante :
en hiver : f = 333,9 /(2x1,5) ~111 Hz soit environ 2 x 57,4.
en été : f = 340,6 /(2x1,5)~114 Hz soit environ 2 x 58,5.
Fréquence de la note suivante :
en hiver : f = 333,9 /(2x0,94) ~177 Hz soit environ 3 x 57,4.
en été : f = 340,6 /(2x0,94)~181 Hz soit environ 3 x 58,5.
La phrase écrite en gras est vérifiée quant à la hauteur des notes. (
compte tenu de la précision des mesures faites sur le schéma).
Par contre en hiver, les fréquences des notes sont un peu inférieures à celles de l'été.
|
|