Implant cochléaire : IRM,  alimentation : pile zinc-air, hydrostatique. Bac STL Biotechnologies Métropole 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Partie I : imagerie par résonance magnétique pour un porteur d'implant cochléaire. I.1. Fonctionnement d'un appareil à imagerie par résonance magnétique (IRM). I.1.1. Préciser le rôle joué par chaque grandeur physique dans la réalisation d'une image par un dispositif d'IRM. Le champ magnétique ( T) permet au noyaux d'hydrogène de s'orienter comme de petits aimants. L'intensité du courant ( A) : une bobine traversée par un courant se comporte comme un aimant ; le champ magnétique est d'autant plus intense que l'intensité est grande. La résistance électrique ( ohm) : plus la résistance électrique est grande, plus les pertes par effet Joule sont importantes ;  l'intensité du courant devra être limitée. La température ( °C ou K) : la résistance de la bobine diminue à basse température ; elle peut s'anuler si le matériau devient supraconducteur. I.1.2. Sachant que la fréquence f de l'onde émise par les noyaux d'hydrogène est proportionnelle à la valeur B de l'intensité du champ magnétique et qu'elle vaut 42,58 MHz pour 1,00 T, calculer la fréquence de l'onde en Hz quand l'appareil est réglé pour 1,50 T. f = k B avec k une constante. 42,58 106 = k *1,00 ; f = 42,58 106 *1,50 = 6,387 107 Hz. I.1.3. Préciser à quel domaine de longueurs d’onde appartient l'onde émise par les noyaux d'hydrogène pour une intensité de champ magnétique de 1,50 T. Vitesse des ondes électromagnétiques dans le vide ou dans l'air : c = 3,00.108 m.s-1. l = c / f = 3,00 108 / (6,387 107) =4,70 m, ondes radioélectriques. I.1.4. Expliquer pourquoi la bobine supraconductrice permet d'obtenir un champ magnétique intense. La résistance électrique de la bbine étant nulle, elle peut être parcourue par des courants intenses ( l'effet Joule est nul). Le champ magnétique est proportionel à l'intensité du courant. I.1.5. Classer les champs magnétiques par intensité croissante. Comparer alors l'intensité du champ magnétique de l'appareil IRM à celles des champs magnétiques courants. 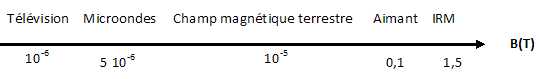Le champ magnétique de IRM et 1,5 millions de fois plus intense que celui d'une télévision, 150 000 fois plus intense que le champ terrestre et 15 fois plus grand que celui des aimants. I.2.Variations de l'intensité du champ magnétique autour de l'appareil IRM. I.2.1. Donner sur le document (zoom de la salle d'examen) un encadrement de la valeur de l’intensité du champ magnétique au point A. 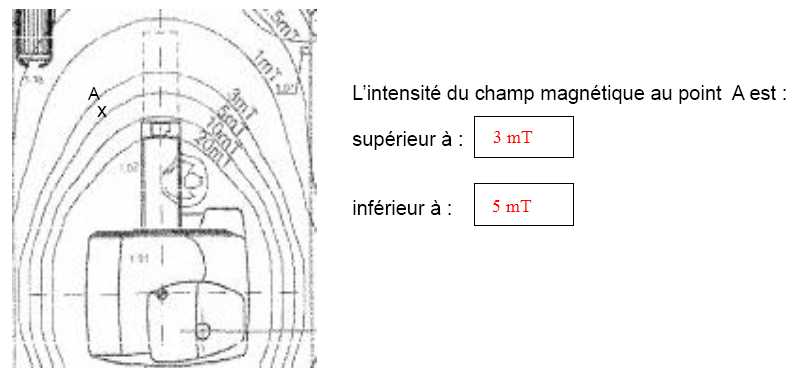I.2.2. Quel est le nom de l'appareil qui permet de mesurer la valeur d'un champ magnétique ? Le teslamètre. I.2.3. Comparer le champ magnétique régnant dans le local de commandes au champ magnétique terrestre. Champ magnétique terrestre 5 10-5 T ; champ magnétique dans la salle de commande : [ 5 10-5 ; 1,5 10-4 T ], c'est à dire une à trois fois supérieur au champ magnétque terrestre. I.2.4. Entourer  le(s) pictogramme(s) qui doivent figurer sur un appareil IRM. 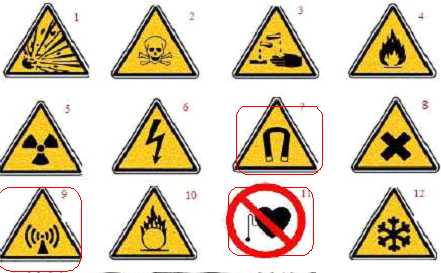Le n°7 indique un champ magnétique, le n°9 un champ de radiofréquence et le n°11 interdit les pacemaker. Partie II : alimentation de l'implant cochléaire. L'implant cochléaire fonctionne grâce à des piles zinc-air p675. L'électrolyte de la pile zinc-air est basique (il y a présence d'ions HO-). Les deux demi équations électroniques modélisant les réactions à chacune des électrodes sont : (1) Zn + 2 HO- = ZnO + H2O + 2 e- (2) O2 + 4 e- + 2 H2O = 4 HO-. II.1.Fonctionnement de la pile zinc-air II.1.1. D'après le schéma suivant et les demi-équations ci-dessus, dans quel sens circule le courant électrique dans le processeur de l'implant ? Justifier votre réponse. 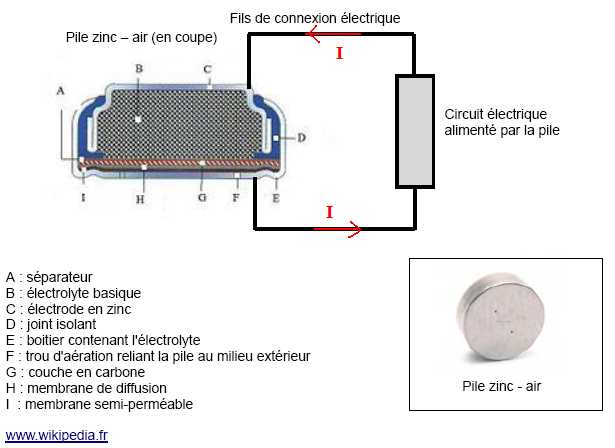Le zinc s'oxyde, il cède des électrons ;  il  constitue la borne négative de la pile. Le courant  parcourt le circuit extérieur en rentrant par l'électrode de zinc. II.1.2. Pour cette électrode de zinc, le couple oxydant/réducteur est ZnO/Zn. Quel est l'autre couple mis en jeu dans la pile ? O2 / HO-. II.1.3. Vérifier à partir des deux demi-équations électroniques que l'équation qui traduit le fonctionnement de la pile est : 2 Zn(s) + O2 = 2 ZnO(s). 2Zn + 4 HO- = 2ZnO +2H2O + 4 e- O2 + 4 e- + 2 H2O = 4 HO-. Ajouter et simplifier. 2Zn + 4 HO- + O2 + 4 e- + 2 H2O = 2ZnO +2H2O + 4 e- + 4 HO-. II.1.4. Justifier le nom de pile zinc-air. Les réactifs sont le zinc et le dioxygène de l'air. II.2.Utilisation de la pile zinc air p675. Les caractéristiques de la pile sont données ( Q = 570 mA h ). L'intensité moyenne du courant circulant dans l'implant vaut I = 8,00 mA. On se propose dans cette étude de déterminer la masse de zinc consommée pendant la durée de fonctionnement de la pile. Données : 1 A.h = 3600 C. Charge élémentaire = 1,6.10-19 C. Nombre d'Avogadro NA = 6,02.1023 mol-1. Masse molaire du zinc : M(Zn) = 65,4 g.mol-1. II.2.1. Évaluer, en heures, l'autonomie de fonctionnement de la pile de l'implant. t = Q / I = 570 / 8,00 = 71,3 h. II.2.2. En déduire la quantité de matière n(e-) d'électrons échangée. n(e-) = 0,570 *3600 / 96500 = 2,1264 10-2 ~2,13 10-2 mol. II.2.3 En utilisant l'équation de fonctionnement de la pile, justifier par un argument simple que le zinc est le réactif limitant. Le dioxygène de l'air ne risque pas de manquer, le zinc est donc le réactif limitant. II.2.4. À partir d'une demi-équation de fonctionnement de la pile, calculer la masse de zinc, m(Zn), consommée lors d'une décharge totale de la pile. n(Zn) = 0,5 n(e-) =1,063 10-2 ~1,06 10-2 mol. m = n(Zn) M(Zn) = 1,063 10-2 *65,4 = 0,695 g. II.2.5. La masse de la pile usée est-elle inférieure, supérieure ou égale à la masse de la pile neuve (la réponse est à justifier) ? Il se forme 1,06 10-2 *(65,4+16) ~0,86 g de ZnO et il disparaît 0,69 g de zinc : la masse de la pile usée est supérieure à la masse de la pile neuve. II.3. Aspects énergétiques de la pile zinc air p675. II.3.1. En effectuant une analyse des unités, choisir parmi les relations suivantes, celle qui relie W, énergie que peut fournir la pile à sa tension U et sa capacité (ou quantité d'électricité disponible) Q. La réponse est à justifier. (1) Q = W.U ; (2) U = W.Q ; (3) W = Q.U. W est en joule, soit une tension ( volt) fois une intensité ( ampère) fois un temps ( seconde). Q est en coulomb soit une intensité (A) fois un temps (s). W = QU (3). II.3.2. Vérifier que l'énergie, en joules, stockée dans la pile p675 vaut Epile = 2,98.103 J. Q = 0,570 Ah = 0,570*3600 =2,052 103 C  et U = 1,45 V. W = Q U = 2,052 103 *1,45 =2,98.103 J ou 2,98 103 / 3600 =  0,827 Wh. II.3.3. L'énergie massique de la pile p675 obtenue par un calcul à effectuer est-elle en cohérence avec les données [245  ; 455 Wh kg-1] ? Masse de la pile : m = 1,85 g. Energie massique E =0,827  /  (1,85 10-3) =447 Wh kg-1. Donc cohérence avec les calculs. II.3.4. Proposer un avantage de la pile p675 par rapport aux autres piles. Sa capacité est supérieure à celle des autres piles, il faudra la changer moins souvent, car elle durera plus longtemps. Partie III : contraintes de l'implant cochléaire. Le système électronique interne de l'implant cochléaire est contenu dans une capsule en céramique placée à l'intérieur de l'oreille interne. Elle est reliée aux électrodes véhiculant le signal électrique en provenance du capteur. Une face de la capsule est soumise à la pression extérieure à l'oreille et l'autre face à la pression intérieure qui demeure égale à la pression atmosphérique. Un porteur d'implant cochléaire décide, après avoir enlevé le processeur externe, de pratiquer un sport aquatique. III.1. Donner la valeur de la pression Pslibre à la surface de l'eau. Justifier brièvement. Pslibre = Patm, la surface de l'eau est en contact avec l'atmosphère. III.2. Le porteur d’implant peut-il pratiquer la natation ? La pression maximale extérieure admissible est Pmax = 5,0 atm. le porteur d'implant peut pratiquer la natation. III.3. Jusqu'à quelle profondeur Hmax le porteur d’implant peut-il nager ? Pmax = 5,0 *1,013 105 = 5,065 105 Pa. Pmax -Patm =reau g Hmax ; Hmax  = 4,052 105 / (1000*9,8) ~41 m. III.4. Le porteur d'implant envisage de nager sous l'eau à une profondeur H = 1,5 m. Quelle serait alors la force exercée sur la capsule en sachant que la pression dans l'oreille interne demeure égale à la pression atmosphérique ? Diamètre de la capsule  : D = 30 mm ; Scapsule = pD2/4 = 3,14 *0,0302 /4 = 7,069 10-4 m2. Pression intérieure : 1,013 105 Pa ;  force intérieure exercée sur la capsule : Fint = 1,013 105 * 7,069 10-4=71,6 ~72 N. Pression extérieure : reau g H + Patm = 1000*1,5*9,8 +1,013 105 = 1,16 105 Pa ;  force extérieure exercée sur la capsule ( en sens contraire de Fint)  : Fext = 1,16 105 * 7,069 10-4=82 N. Fext -Fint ~ 10 N. . .

menu