Mission spatiale
ATV5.
Bac Sti2d 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Objectifs de la mission ATV 5
A.1.1. Indiquer au minimum quatre objectifs de la mission ATV 5.
Apport de vivres et dioxygène aux occupants ; apports de nouveaux
instruments de recherche ; relever l'altitude de la station;
tester le nouveau système LIRIS ; enlever les déchets.
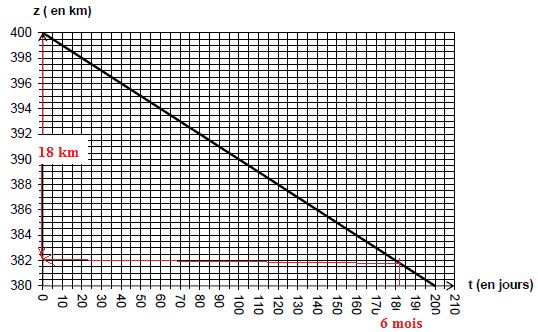
A.1.2. Préciser quelle est la cause de la baisse d’altitude de l’ISS au cours du temps.
Trainée atmosphérique, frottements sur les couhes atmosphériques.
A.1.3. Quelle est la durée approximative de la mission ?
6 mois.
A.1.4. Déterminer
la perte d’altitude totale subie par la Station Spatiale Internationale
au cours de la durée de la mission de l’ATV 5, si celui-ci n’avait pas
relevé régulièrement l’orbite de la Station.
On considèrera qu’un mois dure en moyenne 30,5 jours.
A.2. Préparatifs du lancement de l’ATV par Ariane 5.
A.2.1. Inspection du système d’arrosage de la table de lancement
Lors du décollage de la fusée, les tuyères (orifices de sortie) des
moteurs de la fusée éjectent des gaz très chauds et à très grande
vitesse. Pour protéger la table de lancement des effets néfastes des
gaz d’échappement et atténuer le bruit produit lors du décollage, les
gaz et la table sont arrosés d’eau par l’intermédiaire de 68 bouches de
projection de section S = 126 cm2 chacune. L’alimentation en
eau est assurée par un château d’eau raccordé aux bouches de projection
par un réseau de canalisations muni de vannes dont l’ouverture permet
de déclencher l’arrosage.
Ce système d’arrosage doit assurer un débit volumique d’eau total Dv = 30 m3.s-1 pendant une durée de 50 secondes lors du décollage.
A.2.1.a. Quel doit être le volume VR du réservoir d’eau du château d’eau pour assurer l’arrosage lors d’un décollage ?
30*50 = 1,5 103 m3.
A.2.1.b. Calculer le débit volumique Dv1 de l’eau projetée par une bouche.
30 /68 = 0,44 m3 s-1.
A.2.1.c. En déduire la vitesse v d’éjection de l’eau à chaque bouche de projection au moment du décollage.
v = Dv1 / S = 0,44 / (126 10-4)=35 m s-1.
A.2.1.d. Pour que
le système d’arrosage puisse fonctionner efficacement, la pression
minimale de l’eau au niveau des vannes doit être de 9 bars lorsque
celles-ci sont fermées. En déduire la hauteur minimale du niveau de
l’eau dans le château d’eau.
Pression de l'eau en surface : pA= 1 bar.
pvannes-pA= rg h = (9-1) 105 Pa.
h = 8 105 /(1000 *9,8) ~82 m.
A.2.2. Remplissage des réservoirs du moteur principal de la fusée.
Pour produire la force de poussée nécessaire à la propulsion de la
fusée, ses différents moteurs thermiques utilisent deux substances
chimiques appelées propergols. Les propergols nécessaires au
fonctionnement du moteur principal d’Ariane 5 (le moteur Vulcain) sont
le dihydrogène H2 et le dioxygène O2. Quelques
heures avant le décollage, on procède au remplissage en propergols des
deux réservoirs séparés, situés dans l’étage principal cryotechnique
(EPC) de la fusée.
A.2.2.a. Pendant et
après le remplissage des réservoirs, le dihydrogène est maintenu à la
température T = 20 K et sous la pression P = 2,2 bar. Le dioxygène est
maintenu à T = 90 K sous P = 3,6 bar.
Placer les points correspondant à ces valeurs sur les diagrammes P(T) du document-réponse.
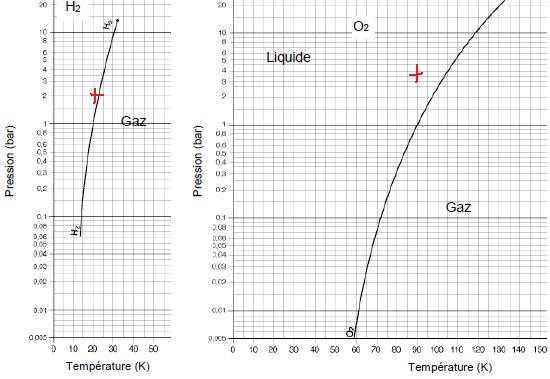
A.2.2.b. En déduire l’état physique des deux ergols stockés dans les réservoirs de l’EPC de la fusée.
Les propergols sont à l'état liquide.
|
|
|
B.1. Étude du fonctionnement du moteur Vulcain lors du lancement.
Certaines caractéristiques du moteur Vulcain sont données en annexe B1.
Lors du fonctionnement, le moteur est alimenté séparément en
dihydrogène et en dioxygène par deux turbopompes de forte puissance
permettant aux propergols d’acquérir un débit, une pression et une
vitesse élevés. Une fois mélangés, les deux propergols explosent,
produisant les gaz d’échappement à l’origine de la force de poussée qui
propulse la fusée.
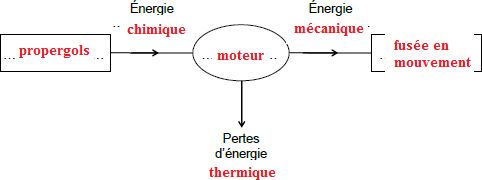
B.1.1. Compléter le
schéma énergétique du moteur à l’aide des termes suivants : moteur -
fusée en mouvement - propergols, et en indiquant la nature des
différentes énergies transférées.
B.1.2. Étude de la réaction
B.1.2.a. Réécrire
l’équation suivante de la réaction chimique qui a lieu entre les deux
propergols du moteur et la compléter à l’aide des coefficients
stoechiométriques appropriés :
.…2…H2 + ……O2 -->…2.H2O
B.1.2.b. Les réservoirs de propergols de la fusée contiennent 1,2.107 mol de dihydrogène et 4,7.106
mol de dioxygène. Calculer la quantité de matière d’eau produite lors
du fonctionnement du moteur, sachant que tout le dioxygène initialement
présent dans le réservoir sera consommé.
4,7 106 *2 = 9,4 106 mol.
B.1.2.c. En déduire que la masse d’eau produite vaut 170 tonnes.
M(eau) = 18 g/mol ; m = 9,4 106 *18 ~1,7 108 g =1,7 102 tonnes.
B.1.2.d. Sachant
que la masse de vapeur d’eau éjectée par le moteur correspond à la
masse de propergols consommée, déterminer, en exploitant la donnée
utile de l’annexe B1, la durée de fonctionnement du moteur.
Débit massique des propergols : 320 kg s-1 = 0,320 t s-1.
170 / 0,320 = 5,3 102 s.
B.2. Étude du décollage et de la phase d’ascension verticale de la fusée.
Dans cette étude, on néglige les forces de frottement dues à l’air et
on considère que la masse de la fusée est constante pendant la phase de
décollage.
B.2.1. On rappelle que l’intensité de la pesanteur au niveau du sol vaut g = 9,81 m.s-2.
Sachant que la masse de la fusée au décollage est de 774 tonnes, calculer l’intensité P du poids total de la fusée au décollage.
P = mg = 774 103 *9,81 = 7,59 106 N. (ou 7,59 103 kN).
B.2.2. L’intensité
de la force de poussée totale produite par les moteurs des deux EAP et
du moteur Vulcain de la fusée au décollage vaut FP = 13.103 kN.
Représenter, à partir du centre de gravité G, les forces agissant sur la fusée lors du décollage.
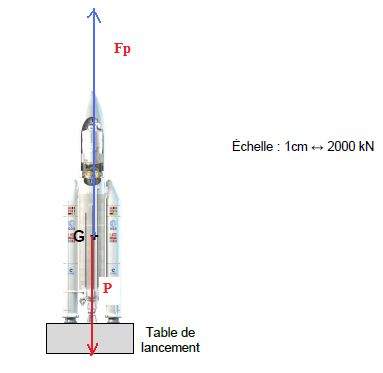
La chronologie du décollage et de l’ascension verticale de la fusée est détaillée en annexe B2.
B.2.3. Montrer que l’accélération a de la fusée au décollage et lors de la phase d’ascension verticale est égale à 7,0 m.s-2.
FP-P = ma ; a = FP/m-g = 13 106 / (774 103) -9,81 =6,98 ~7,0 m s-2.
B.2.4. En déduire l’altitude z atteinte par la fusée en fin d’ascension verticale.
z = ½a Dt2+ vi Dt +zi.
vi =0, vitesse initaiel ; zi = 0, altitude initiale, Dt = 13 s, durée écoulée depuis le début de l'ascension.
z = 3,5 (13)2 = 5,9 102 m.
B.2.5. En exploitant l’annexe B1, montrer que le travail Wvulc de la
force de poussée produite par le moteur Vulcain lors de l’ascension
vaut 6,5.108 J.
Force de poussée du moteur Vulcain : F = 1100 kN = 1,1 106 N.
W = F z = 1,1 106 *5,9 102 = 6,5.108 J.
B.2.6. En déduire l’énergie Eth nécessairement libérée durant
l’ascension par la réaction chimique qui a lieu entre les propergols du
moteur Vulcain.
Rendement du moteur : 40 %.
Eth = W / 0,40 = 6,5 108 /0,40 = 1,6 109 J.
|
|
|
|
B.3. Traitement de l’eau polluée.
Dans les instants qui suivent le décollage, on observe une forte
concentration en chlorure d’hydrogène HCl sur le pas de tir. Le
lendemain du décollage, les tunnels d’évacuation des gaz d’échappement
de la fusée, creusés dans la table de lancement, sont remplis d’eau
polluée acide qu’il faut évacuer. Pour ce faire, l’eau doit d’abord
être neutralisée pour obtenir un pH aux alentours de 7 : des bases
comme la soude sont ajoutées. À cause de ce processus de neutralisation
chimique, les tunnels d’évacuation sont inaccessibles pendant un mois
après chaque vol.
B.3.1. Quelle est
la nature chimique de la solution formée par dissolution du chlorure
d’hydrogène dans l’eau projetée sur le pas de tir de la fusée : acide,
basique ou neutre ?
La solution est une solution d'acide chlorhydrique, donc acide.
B.3.2. Pour éviter
que cette solution ne pollue l’environnement, faut-il augmenter ou
diminuer son pH avant de l’évacuer ? Faut-il augmenter ou diminuer la
concentration en ions H3O+ de la solution ? Que font les techniciens pour cela ?
Il faut augmenter son pH juqu'à environ 7, c'est à dire diminuer la concentration en ion oxonium H3O+par ajout d'une base.
B.3.3. Écrire
l’équation de la réaction acido-basique qui a lieu lorsqu’on neutralise
la solution sachant qu’elle met en jeu les deux couples acide - base : H2O / OH- et H3O+/ H2O.
H3O+aq + OH- aq --> 2 H2O(l).
C.1. Production et stockage de l’énergie nécessaire au fonctionnement du système de guidage de l’ATV.
Suite à son lancement par Ariane 5, l’ATV vole librement vers la
station spatiale en orbite circulaire à 400 km de la surface de la
Terre et s’y amarre.
Durant cette phase de vol libre, les 16 panneaux solaires de l’ATV,
répartis sur les 4 ailes solaires de l’appareil, et un ensemble de 4
batteries nickel-cadmium (Ni-Cd) fournissent l’énergie nécessaire au
fonctionnement du système de guidage automatique de l’appareil.
L’ATV en rotation rapide autour de la Terre est éclairé par le soleil
pendant 61 minutes : les panneaux alimentent alors le système de
navigation de l’ATV et rechargent les batteries.
Lorsque l’ATV est masqué par l’ombre de la Terre, durant 31 minutes, ce sont les batteries qui alimentent le système de guidage.
C.1.1. Compléter la
chaîne énergétique du dispositif pendant la journée à l’aide des termes
suivants : système de guidage - panneaux solaires - Soleil - batteries,
et en indiquant la nature des différentes énergies transférées.
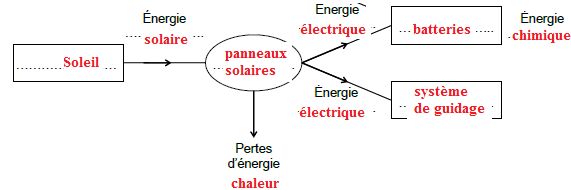
C.1.2. Le fonctionnement du système de guidage de l’ATV nécessite une puissance Psg = 900 W.
C.1.2.a. Pendant la journée, l’éclairement énergétique, supposé constant, reçu par les panneaux est de 1370 W.m-2.
En déduire, à l’aide de l’annexe C1 :
la puissance Pa reçue par les panneaux, la puissance Pu qu’ils fournissent, que la puissance reçue par les batteries vaut Pbat = 6,9 kW.
Surface totale des panneaux 33,6 m2.
Pa =33,6 *1370 =4,60 104 W.
Rendement des panneaux : 17 % ; Pu = Pa *0,17 = 4,60 104 *0,17 =7,8 103 W = 7,8 kW.
Pbat = Pu -Psg =7,8 -0,90 = 6,9 kW.
C.1.2.b. Calculer
l’intensité du courant débité par l’association de batteries pour
alimenter le système de guidage lorsque l’ATV n’est pas éclairé,
sachant que la tension aux bornes de l’ensemble vaut U = 57,6 V.
I = Psg /U = 900 / 57,6 =15,6 A.
C.1.2.c. Déterminer la charge Q consommée par le système de guidage lorsque l’ATV n’est pas éclairé.
Q = I t = 15,6* 31*60 =2,9 104 C soit 2,9 104 / 3600 = 8,1 Ah pour un tour.
C.1.2.d. La charge
initiale de l’ensemble des batteries étant de 160 A.h, ces batteries
permettent-elles de faire fonctionner correctement le système de
guidage ? Justifier la réponse.
Les batteries sont régulièrement rechargées par les panneaux solaires durant 61 min par tour.
Le système de guidage ne consomme que 8,1 Ah pendant 31 min, valeur 20 fois inférieure à la charge initiale des batteries.
C.1.3. L’ATV est également équipé de 4 piles Li-MnO2
non rechargeables fournissant l’énergie nécessaire au fonctionnement
des capteurs optiques de rendez-vous lors de la phase d’amarrage du
véhicule à l’ISS.
Chaque pile est constituée de deux électrodes, l’une en carbone C et en lithium Li, l’autre en dioxyde de manganèse MnO2 (voir document réponse DR5). Lors du fonctionnement de la pile, les atomes de lithium Li se transforment en ions lithium Li+ qui quittent l’électrode en carbone et traversent l’électrolyte pour venir s’insérer dans la structure du dioxyde de manganèse.
Préciser sur le document réponse DR5 :
le sens de déplacement des ions lithium dans l’électrolyte ;
le sens de circulation des électrons et du courant I dans le circuit électrique ;
le nom de chaque électrode, le nom de la réaction qui a lieu à
chaque électrode, ainsi que l’équation de la réaction qui a lieu à
l’électrode en carbone et en lithium.
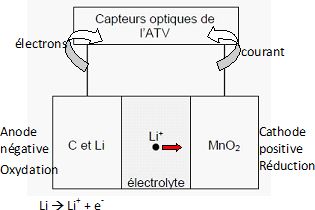
|
C.2. Mise en oeuvre du système optique lors de la phase d’approche et d’amarrage de l’ATV à la station spatiale.
Pour s’amarrer à la station, l’ATV 5 est équipé du système optique
LIRIS (Laser Infrared Imaging Sensors) constitué de 3 caméras et d’un
dispositif à émetteurs-récepteurs laser. Ce système sophistiqué permet
d’obtenir des images 3D de la station spatiale et de calculer en temps
réel la distance et la vitesse de l’ATV par rapport au point d’amarrage
de la station.
C.2.1. Les trois
caméras du système LIRIS détectent les ondes électromagnétiques émises
par la station spatiale dont l’énergie E est comprise entre 1,99.10-22 J et 2,48.10-19 J.
C.2.1.a. Déterminer l’intervalle des longueurs d’ondes l détectées par les caméras du système LIRIS. Justifier.
l = hc / E =6,63 10-34 *3,00 108 /(1,99 10-22)~ 1,0 10-3 m.
l = hc / E =6,63 10-34 *3,00 108 /(2,48 10-19)~ 8,0 10-7 m.
[8,0 10-7 m ; 1,0 10-3 m ] appartient au domaine infrarouge, limité par le visible et les micro-ondes.
C.2.2. Dès que
l’ATV s’est rapproché à moins de 250 m de la station, chaque émetteur
du système LIRIS envoie, à intervalles de temps réguliers, une brève
impulsion laser en direction de la station spatiale qui la réfléchit
dans la direction du récepteur correspondant de l’ATV . Le système
LIRIS mesure la durée Dt
écoulée entre l’émission de chaque impulsion laser et la réception de
son écho pour calculer la distance et la vitesse de l’ATV par rapport à
la station.
Aurait-on pu utiliser des émetteurs-récepteurs à ultrasons pour réaliser l’amarrage de l’ATV à la station ? Justifier.
Non, les ultrasons sont des ondes mécaniques qui ne se propagent pas dans le vide.
|
|