Le
diagnostic médical : rayons X, RMN, technique Western Blot. Bac STL
2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Partie A :
la radiographie par rayons X.
Un patient souffre d’une talalgie droite après effort (douleur au talon
droit). Son médecin traitant lui prescrit une radiographie des talons.
Une radiographie par rayons X permet de visualiser le squelette et, par
exemple, d’observer une fracture pour mieux la soigner. Elle permet
également de détecter des tissus endommagés par une maladie : les
radiographies des poumons, couramment
pratiquées, donnent au médecin d’importantes informations sur l’état de
santé du patient.
1. Les ondes
électromagnétiques.
1.1
Le symbole l
est associé à la longueur d’onde.
Donner l’unité de cette grandeur dans le « système international ».
Une longueur d'onde s'exprime en mètre.
1.2
Compléter le document suivant, afin de situer les domaines des
différentes ondes électromagnétiques (rayons X, rayonnement
visible, rayonnement infrarouge, rayonnement ultra-violet, rayons
gamma).
 2. Production de rayons X.
2. Production de rayons X.
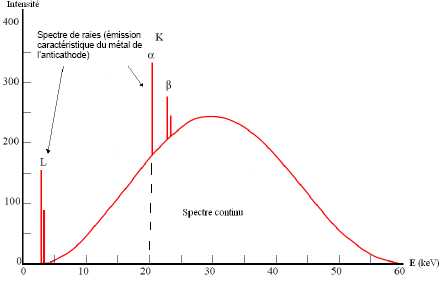
La production de rayons X est réalisée à l’aide d’un tube de Coolidge
dont l’anticathode est en rhodium. L’atome de rhodium a pour symbole 10345Rh
. Son spectre d’émission est présenté.
2.1.
Donner la composition du noyau atomique de rhodium.
45 protons ; 103-45 = 58 neutrons.
L’énergie de la raie d’émission Kß, de
l’anticathode au rhodium est EKß = 22,81 keV.
2.2. Convertir
cette énergie en joules.
22,81 103 *1,60 10-19 =
3,65 10-15 J.
2.3.
Calculer la valeur de la longueur d’onde lKß
associée à cette radiation.
lKß
= h c / EKß
=6,62 10-34 *3,00 108 /(3,65 10-15) =5,44 10-11 m.
2.4.
Montrer que cette raie Kß est due à
une transition électronique de la couche M vers la couche K.
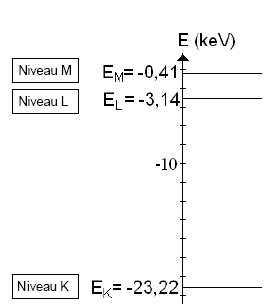
EM-EK =-0,41 -(-23,22) =
22,8 keV.
2.5.
Déterminer la valeur de l’énergie de la raie Ka. 20
keV.
2.6.
La longueur d’onde lKa
de cette raie est-elle supérieure ou inférieure à la longueur d’onde lKß
? Justifier.
lKa
> lKß
car EKß>
EKa.
3. Absorption des rayons X par
les tissus organiques - qualité de l’image.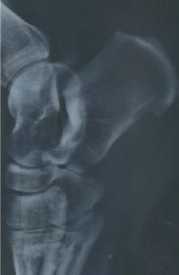
3.1.
En étudiant la radiographie du talon du patient, on distingue deux
types de zone (claire ou sombre). Que matérialisent ces zones ?
Préciser le constituant qui absorbe le plus les rayons X, d’après cette
radiographie.
3.2.
Proposer une explication justifiant la différence d'absorption qui
apparaît sur la radiographie.
Les os contiennent essentiellement du phosphore (symbole 15P)
et du calcium (symbole 20Ca). Les tissus « mous
» sont plutôt constitués de carbone, hydrogène, oxygène et azote.
Plus le numéro atomique de l'élément est grand,plus les rayons X sont
absorbés. Les os apparaissent en zone clair et les tissus mous en zones
sombre.
On donne la couche de demi-absorption (CDA) de différents tissus
(graisse et muscle) en fonction de l’énergie des photons X qui les
traversent.
| E(keV) |
20 |
30 |
40 |
50 |
60 |
| CDA
(graisse ) cm |
1,5 |
2,7 |
3,7 |
4,5 |
5,1 |
| CDA
(muscle) cm |
0,9 |
1,7 |
2,4 |
3,0 |
3,3 |
La
couche de demi-absorption (CDA) d’un tissu correspond à l’épaisseur
pour laquelle la moitié du flux incident (F0)
de rayons X a été absorbée.
3.3.
Quel est le tissu corporel qui absorbe le plus les rayons X ? Justifier
votre réponse.
Les muscles absorbent plus les rayons X que la graisse. La CDA des
muscles est inférieure à celle de la graisse.
Le coefficient d’absorption est donné par la relation : µ = ln(2) / CDA.
3.4.
Calculer la valeur du coefficient d’absorption µ pour la graisse et
pour le muscle sous un rayonnement de 40 keV.
µmuscle = ln2 / 2,4 = 0,288 ~0,29 cm-1
; µgraisse
= ln2 / 3,7 = 0,187 ~0,19 cm-1.
Données :
On appelle FM
le flux sortant pour le muscle et FG
le flux sortant pour la graisse.
Le flux sortant F
a pour expression F
=F0exp(-µd) avec
d = 4,0 cm, épaisseur du tissu traversé,
et F0 = 0,5 W.m–2
à 40 keV, flux entrant dans le tissu.
3.5.
Calculer la valeur des flux FG et FM puis,
compléter le tableau.
| Tissus
biologiques |
|
Unités |
valeurs
à 40 kHz |
| Graisse |
µG |
cm-1 |
0,19 |
| FG |
W
m-2
|
0,24 |
| Muscle |
µM |
cm-1 |
0,29 |
| FM |
W
m-2 |
0,16 |
Pour obtenir
des radiographies de bonne qualité, le contraste radiologique C doit
être élevé. Il est défini pour le muscle et la graisse par la relation
: C = (FG-FM) / (FG+FM).
3.6.
Calculer la valeur du contraste pour des photons X d’énergie 20 keV.
Calculer également la valeur du contraste pour des photons d’énergie 60
keV.
| Tissus
biologiques |
|
20
keV |
60
keV |
| Graisse |
FG |
0,079 |
0,26 |
| Muscle |
FM |
0,023 |
0,22 |
Cgraisse
= (0,079-0,023) / (0,079 +0,023) =0,55.
Cmuscle = (0,26-0,22)
/ (0,26 +0,22) =0,083.
3.7. En déduire
s’il faut utiliser des rayons de faible énergie (20 keV) ou de grande
énergie (60 keV) pour différencier, au cours d’une radiographie X, le
muscle de la graisse.
Le contraste est plus élevé pour les rayons X d'énergie 20
kHz. On choisit ces derniers.
|
|
|
Partie B : l’examen par résonance
magnétique nucléaire.
Le médecin d’un patient suspecte la présence d’une tumeur cérébrale et
l’oriente vers un neurologue. Celui-ci lui prescrit un examen par IRM
(Imagerie par Résonance Magnétique).
1. Principe
de l’IRM.
1.1 Donner
les avantages et les inconvénients d’un examen IRM.
Avantages
: faible consommation d'énergie ; image de grande précision, sans
danger pour le patient ( absence de traceur radioactif ).
Inconvénients
: examen assez long, l'intensité sonore est élevée. Le coût des
appareils est élevé.
1.2
Citer trois sources différentes de champs magnétiques.
Electroaimants, aimants naturels ( magnétite) ou artificiels ; champ
magnétique terrestre.
1.3
Quel type de source est utilisé pour l’IRM ?
Electroaimants avec bobines supraconductrices.
1.4
Donner l’avantage de la supraconduction.
L'effet Joule étant minimisé, il n'est pas nécessaire de refroidir les
bobines.
Dans un examen par IRM, le champ magnétique est créé par un solénoïde.
2. Champ
magnétique créé par un solénoïde.
Les caractéristiques du solénoïde utilisé sont indiquées.
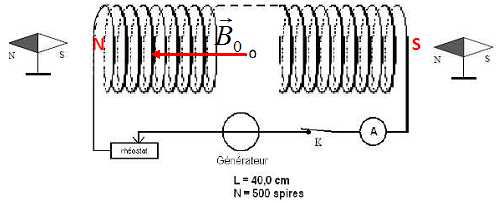
2.1 Nommer l’appareil, non représenté sur le schéma, permettant de
mesurer un champ magnétique. Le teslamètre.
Lorsque l’interrupteur K est fermé, un courant électrique continu
circule dans le solénoïde. Les petites aiguilles aimantées sur pivot
prennent alors la direction et le sens indiqué.
2.2
Compléter, en justifiant votre raisonnement en indiquant :
a. la nature magnétique des faces du solénoïde (face nord et face sud)
b. le vecteur champ magnétique B0 au centre O du
solénoïde.
L'extrémité S de la boussole pointe vers une face nord ; l'extrémité n
de la boussole pointe vers une face de nom contraire, sud. A
l'extérieur du solénoïde, les lignes de champ magnétiques sortent par
la face nord et rentrent par la face sud du solénoïde.
Au cours d’une séance de travaux pratiques, on se propose d’étudier
l’influence de l’intensité du courant électrique sur la valeur du champ
magnétique créé en son centre (le point O). Le solénoïde est considéré
comme long. Les résultats de l’expérience sont reportés dans le tableau
suivant :
| I(A) |
0,00 |
0,51 |
1,02 |
1,45 |
1,98 |
3,20 |
3,78 |
4,25 |
| B(mT) |
0,00 |
0,80 |
1,61 |
2,28 |
3,12 |
5,04 |
5,95 |
6,69 |
2.3 On rappelle que
pour un solénoïde suffisamment long : B =µ0NI /
L.
On considérera que la perméabilité magnétique de l’air est la
même que celle du vide µ0.
Préciser le nom des grandeurs N, L et I utilisées dans cette formule.
Donner les unités de L et de I dans le système international.
I : intensité du courant ( ampère) ; N : nombre de spire de la bobine ;
L : longueur de la bobine ( m).
On effectue avec une calculatrice une régression linéaire modélisant la
courbe B = f(I). On obtient les résultats suivants : B = 1,57 I +0,142
( I en A et B en mT)
2.4
Peut-on considérer que les résultats expérimentaux sont en accord avec
la formule ? Justifier.
Oui, B est une fonction afine de l'intensité : le champ magnétique est
proportionel à l'intensité du courant I. le coefficient de
proportionalité vaut µ0N/L = 4*3,14 10-7
*500 / 0,40 = 1,57 10-3 T A-1.
Au cours de la même séance de travaux pratiques, grâce à leurs mesures,
les élèves ont déterminé expérimentalement la perméabilité magnétique
du vide µ0. Leurs résultats sont reportés dans
le tableau suivant.
| µ0(T
m A-1) |
1,23
10-6 |
1,20
10-6 |
1,31
10-6 |
1,25
10-6 |
1,28
10-6 |
1,27
10-6 |
1,24
10-6 |
1,23
10-6 |
1,25
10-6 |
2.5 À l’aide de la
calculatrice, indiquer la valeur moyenne de la perméabilité magnétique
µ0(moyen) de cette série de mesures. µ0 moyen
=1,24 10-6
T
m A-1.
L’écriture
du résultat du mesurage a pour expression µ0=
µ0 moyen ± tnsn-1
/ n½.
avec tn =2,5 coefficient de Student, n nombre de
mesures effectuées,
sn-1 écart type
expérimental ayant pour valeur 3,22 x 10–8 U.S.I.
2.6
Calculer la valeur de l’incertitude associée au mesurage de µ0,
avec un niveau de confiance de 95 %.
± tnsn-1
/ n½ =± 2,5 *3,22 10-8 /9½
=2,7 10-8 ~3 10-8
T m A-1.
µ0=(1,24±0,03
)10-6 T m A-1.
2.7 Sachant que la
valeur théorique est µ0 théo = 4p×10–7
T.m.A–1, conclure sur la mesure effectuée.
µ0
théo =1,26 10-6
T.m.A–1appartient à l'intervalle [ 1,21 10-6
; 1,27 10-6] : la mesure éffectuée est correcte..
|
|
|
|
Partie C : l’étude virologique
par la technique « Western Blot ».
La technique « Western Blot » permet la détection d’anticorps anti-VIH,
basée sur la caractérisation d’anticorps contre chacune des protéines
virales. En vue de confirmer la séropositivité ou d’observer
l’évolution des anticorps du patient, cette méthode a été appliquée à
différentes dates. Les résultats de l’analyse montrent que le patient
n’est finalement pas infecté par ce virus.
Cette technique est utilisée, lors d’une recherche virologique du VIH,
pour confirmer le résultat obtenu par un test habituel qui s’est révélé
positif.
Dans le cadre de poursuite d’études dans le domaine des
biotechnologies, on peut être amené à utiliser ce procédé
d’identification (sur des substrats moins dangereux). On s’intéressera
à quelques aspects techniques intervenant dans la méthode « Western
Blot ».
On donne l’organigramme des différentes étapes de cette technique.
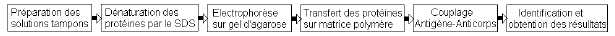
1.
Préparation de la solution tampon.
Les solutions tampon sont très souvent utilisées en biochimie. Leur pH
varie peu lors d’une addition modérée d’acide ou de base, ou lors d’une
dilution.
1.1
Rappeler la définition d’une espèce acide.
Un acide est une espèce, ion ou molécule, susceptible de céder un
proton H+.
1.2 a)
Rappeler la relation liant le pH d’une solution à la concentration en
ion oxonium [H3O+] pour
une solution diluée.
pH = - log [[H3O+].
On admet que cette relation est valable pour la solution d'acide
chlorhydrique utilisée ( c = 0,40 mol/L).
b)
Déterminer le pH de cette solution.
Pour un acide fort : pH = -log c = -log 0,40 ~0,40.
On
donne la réaction acido-basique qui a lieu lors de la préparation de
cette solution tampon : Tris + H3O+
= TrisH+ + H2O
1.3 Montrer
que la masse molaire de la molécule appelée « Tris » est 149,0 g.mol–1.
N(CH2-CH2-OH)3
ou C6H15O3N
: M = 6*12+15+3*16+14=149,0 g.mol–1.
1.4 La réaction
étant considérée comme totale, déterminer les quantités finales en TrisH+
et en Tris exprimées en moles.
m = 37,25 g de TRIS soit n = 37,25 /149 = 0,250 mol.
418 mL d'acide chlorhydrique à 0,40 mol/L : n' = 0,418*0,40 = 0,167
~0,17 mol.
L'acide chlorhydrique est en défaut : n(TRIS) finale =
0,250-0,167 =0,083 mol ; n(TRISH+)
finale =0,167 mol.
1.5 Calculer alors
les concentrations finales de ces deux espèces. V = 0,500 L.
[TRISH+] = 0,167 / 0,5 = 0,334 mol/L ; [TRIS]=0,083
/0,500 = 0,166 mol/L.
1.6 Sachant que le
pH de cette solution tampon est donné par la relation : pH = 8,1 + log([TRIS] / [TRISH+], vérifier que la valeur du pH
de la solution ainsi préparée est pH = 7,8.
pH = 8,1 + log(0,166 / 0,334)=7,8.
2.
Électrophorèse.
Une fois les protéines dénaturées par le SDS (dodécylsulfate de
sodium), elles sont placées en milieu basique et prennent une forme
anionique. Elles sont déposées dans des puits creusés dans un gel
d’agarose prévus à cet effet. Des électrodes, en contact avec le gel
sont ensuite reliées à une source de tension continue. Un schéma de
l’électrophorèse est donné.
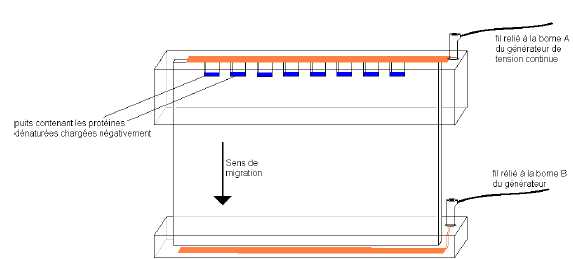
2.1
Rappeler la nature des porteurs de charge circulant dans les métaux
puis dans le gel d’agarose.
Les électrons sont les porteurs de charge circulant dans les métaux.
les ions sont les porteurs de charges du gel d'aragose.
2.2
Attribuer pour les bornes du générateur A et B, la polarité (+ ou -)
afin que les protéines puissent migrer dans le sens indiqué. Justifier.
Les protéines négatives migrent vers le fil B relié au pôle
positif du générateur.
2.3
À l’aide de l’affichage de l’appareil ( 184 V ; 272 mA ), calculer la
puissance électrique fournie par le générateur.
P = 184*0,272 = 50,0 W.
2.4
En déduire la valeur en joules de l’énergie électrique fournie par le
générateur sachant que la durée du processus de séparation des
protéines est de 56 minutes.
E = P t = 50,0 *56*60 = 1,68 105 ~1,7 105
J.
3. Transfert
sur une matrice polymère.
Une fois l’électrophorèse effectuée, les protéines fixées sur le gel,
sont ensuite transférées grâce à un générateur électrique sur un
polymère de masse molaire Mp = 17,2 kg.mol–1.
3.1
Rappeler la définition d’un polymère et du degré de polymérisation (n).
Un polymère est une macromolécules obtenue par polymérisation de n
motifs élémentaires, le monomère.
Le degré de polymérisation est le nombre de monomères constituant le
polymère.
3.2
Entourer un motif de ce polymère.

3.3
Après avoir calculé la masse molaire de ce motif, montrer que l’indice
de polymérisation du polymère étudié est n = 269.
M(monomère) =2*12+2+19*2 = 64 g/mol ; n = 17,2 103
/ 64 =269. |
4. Identification des protéines
par des anticorps.
Les protéines du virus (antigènes), une fois déposées sur le polymère,
sont mises en présence d’anticorps spécifiques au virus recherché,
synthétisés par un animal (lapin). Après interaction
antigène-anticorps, la matrice polymère est rincée, et mise en présence
d’anticorps « anti-lapin » portant un traceur. Les premiers traceurs
étaient radioactifs et portaient un noyau d’iode 125 ou de tritium
(hydrogène 3). La révélation se faisait avec une plaque photographique
et durait quelques heures avec les traceurs incluant un noyau d’iode
125 et quelques semaines pour ceux marqués au tritium.
Données :Iode 125 : 12553I.
Extrait de la classification périodique : 50Sn,
51Sb, 52Te, 53I,
54Xe, 55Cs, 56Ba.
4.1
Donner la composition d’un noyau d’iode 125.
53 protons et 125-53 = 72 neutrons.
4.2
La radioactivité de l’iode 125 est de type ß+.
Indiquer le nom et le symbole de la particule émise.
Positon 01e.
4.3
Écrire l’équation de désintégration nucléaire du noyau d’iode 125.
Préciser les règles de conservation utilisées.
12553I
--> 12552Te
+01e.
Conservation de la chaege et conservation du nombre de nucléons.
Le
temps de demi-vie (appelé aussi période radioactive) de l’iode 125 est
de 59 jours. Celle du tritium est de 12,3 ans.
4.4
Rappeler la définition du temps de demi-vie.
La demi-vie est la durée au bout de laquelle l'activité initiale est
divisée par deux.
Ce sont des rayons g
qui sont à l’origine de la révélation photographique avec la méthode au
tritium.
4.5
Quelle en est leur origine ?
Le noyau fils es dans un état excité. Il libère son surplus d'énergie
sous forme de rayons g
afin
de revenir à l'état fondamental de moindre énergie.
4.6
Justifier le fait que la révélation grâce aux noyaux d’iode 125 soit
plus rapide que dans le cas du tritium.
La demi-vie de l'iode 125 est très inférieure à celle du tritium. |
|