L'alanine en
infrarouge. Bac S Polynésie 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
1. L’alanine.
La formule semi-développée de l’alanine est :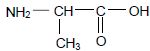
1.1. Molécule d’alanine.
1.1.1. Justifier que le nom donné à l’alanine en nomenclature officielle est l’acide 2-aminopropanoïque.
Le squelette carboné compte trois atomes de carbone., d'où propa.
L'alanine possède une fonction acide carboxylique : d'où acide.....propanoïque.
L'alanine possède un groupe amine port par le carbone n°2, d'où acide 2-aminopropanoïque.
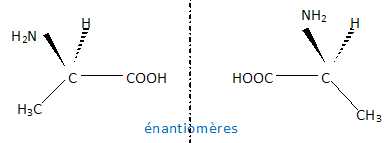
1.1.2. Pourquoi l’alanine présente-t-elle des stéréoisomères ?
Donner leur représentation de Cram et préciser le type de relation de stéréoisomérie qui les lie.
Le carbone n°2 portant 4 substituants différents est asymétrique. Il existe donc deux énantiomères.
1.2. Synthèse de l’alanine.
L’une des voies de synthèse de l’alanine consiste à faire réagir
l’ammoniac avec l’acide 2-bromopropanoïque. Le bilan de la synthèse
peut être modélisé par la réaction chimique d’équation :
1.2.1. Déterminer la catégorie de cette réaction.
Substitution de Br par NH2.
1.2.2. Dans les
conditions opératoires choisies pour la synthèse, le rendement est de
80 %, l’ammoniac, réactif le moins onéreux, étant mis en excès.
Quelle masse d’acide 2-bromopropanoïque faut-il utiliser pour synthétiser 1,0 kg d’alanine ?
M( acide 2-bromopropanoïque) = 3*12 +5+2*16+80 =153 g/mol.
M(alanine) =3*12+7+2*16+14=89 g/mol.
Quantité de matière d'alanine : n = 1,0 103 / 89 =11,236 mol.
Quantité de matière d'acide 2-bromopropanoïque : n / 0,80 = 11,236 / 0,80 =14,045 mol.
Masse d'acide 2-bromopropanoïque : 14,045 *153 =2149 g ~2,1 kg.
|
|
|
1.3. Spectres IR et RMN du proton de l’alanine.
On dispose des spectres IR et RMN du proton de deux composés dont l’un
des deux est l’alanine. Identifier les spectres correspondant à
l’alanine. Justifier.
Spectre RMN (obtenu dans des conditions permettant d’éliminer les signaux relatifs à N-H et à O-H)
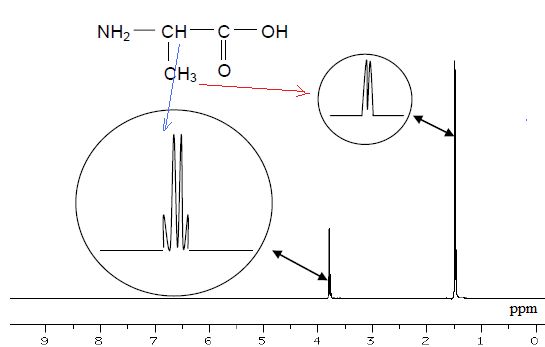
CH : quadruplet, le carbone voisin porte 3 protons.
CH3 : doublet : le carbone voisin porte un proton.
Les spectre IR proposés sont assez semblables et ne permettent pas de conclure.
|
|
|
|
2. Spectroscopie infrarouge
Les techniques de spectroscopie reposent sur l’interaction entre un
rayonnement électromagnétique et la matière. L’absorption de certaines
radiations infrarouges par une molécule organique provoque des
vibrations moléculaires. On s’intéresse aux vibrations d’élongation qui
correspondent à une modification périodique de la distance entre deux
atomes liés. Elles peuvent être étudiées en modélisant une liaison
covalente par un oscillateur mécanique.
2.1 Exemple d’oscillateur mécanique.
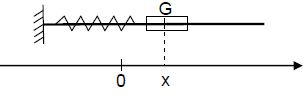
Un solide de masse m pouvant glisser sans frottement sur une tige
horizontale et accroché à un ressort de raideur k comme l’indique la
figure ci-dessous, constitue un exemple oscillateur mécanique.
La position du solide est repérée sur l’axe Ox par l’abscisse de son centre d’inertie G.
On réalise trois expériences pour étudier l’influence de différents
paramètres sur les oscillations. Le solide est écarté de sa position
d’équilibre, repérée par l’abscisse x = 0, de façon à étirer le
ressort, puis est lâché sans vitesse initiale. L’évolution de la
position x en fonction du temps est représentée ci-après pour chaque
expérience.
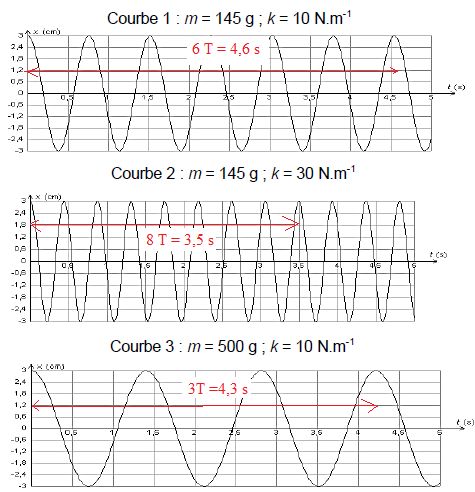
Discuter,
d’après les courbes 1 à 3, de l’influence de la masse m du solide et de
la constante de raideur k du ressort sur les oscillations.
Courbes 1 et 2 : masse constante, la raideur triple, la période est divisée par environ 3½.
La période est inversement proportionnelle à la racine carrée de la raideur.
Courbes 1 et 3 : raideur constante, la masse est multipliée par 3,45, la période est multipliée par 1,86 soit 3,45½.
La période est proportionnelle à la racine carrée de la masse.
2.2 Vibration d’une liaison covalente.
La vibration de la liaison de covalence liant deux atomes A et B de masses respectives mA et mB est due à l’absorption d’une radiation électromagnétique dont le nombre d’onde s s’exprime par la relation :
 masse réduite du système des deux atomes A et B calculée à partir des masses atomiques respectives mA et mB des atomes A et B et exprimée en g ;
a: constante de force de la liaison exprimée en g.s-2 ;
c : célérité de la lumière dans le vide en cm.s-1, égale à 3,00 x1010 cm.s-1 ;
s : nombre d’onde de la radiation absorbée exprimée en cm-1.
Données :
- Masses atomiques :
mH = 1,67 x 10-24 g ; mC = 1,99 x 10-23 g ; mO = 2,66 x 10-23 g ;
Constante de force de la liaison C – H : a = 5,0 x 105 g.s-2.
Relation liant longueur d’onde et nombre d’onde : s =1 / l.
2.2.1 Retrouver l’unité du nombre d’onde s par une analyse dimensionnelle.
a s'exprime en g s-2 ; µ s'exprime en g ; a / µ s'exprime en s-2 ; [a / µ]½ s'exprime en s-1.
1 / c s'exprime en s cm-1 ; s s'exprime en cm-1.
2.2.2 Calculer le nombre d’onde correspondant à la vibration d’élongation d’une liaison C – H. Comparer le résultat aux données.
µ = 1,67 x 10-24 x 1,99 x 10-23 / ( 1,67 x 10-24+1,99 x 10-23) =1,54 10-24 g.
s = 1 / (2*3,14 *3,00 1010) *[5,0 105 / (1,54 10-24)]½ =3024 ~3,0 103 cm-1, en accors avec les données.
2.2.3 Dans les
acides carboxyliques, l’absorption du rayonnement IR par la liaison
simple C – O du groupe d’atomes C – OH est observée vers
1300 cm-1 alors que celle de la liaison double C = O est observée aux alentours de 1700 cm-1.
Sachant que les masses réduites des groupes d’atomes C – OH et C = O, peuvent être considérées comme étant égales, proposer une
explication.
La constante de force d'une liaison double est supérieure à celle d'une liaison simple.
|
|