Coucher de soleils sur Tatooine. Bac S Métropole 2016. . . Dans la saga Star Wars, deux héros, Luke et Anakin Skywalker, ont passé leur enfance sur la planète Tatooine. Cette planète désertique a la particularité d’être en orbite autour de deux étoiles : Tatoo 1 et Tatoo 2. On se propose de déterminer quelques caractéristiques de cette planète et de ses deux étoiles à partir de données extraites du film. Masse de la terre : 6,0 1024 kg; rayon terrestre : 6,4 103 km. Masse du soleil : 2,0 1030 kg; rayon du soleil : 7,0 105 km. L’orbite de Tatooine. Impossible d'évoquer la célèbre planète Tatooine, repère de brigands galactiques sur lequel règne le fameux Jabba le Hutt, sans parler de ses deux soleils (ou étoiles). Cette particularité n'est pas si étonnante quand on considère que les deux tiers des étoiles visibles à l'oeil nu font partie d'un système multiple. Le problème n'est donc pas de trouver une étoile double, mais de comprendre comment une planète peut évoluer dans un tel système. (…) L'orbite de Tatooine pourrait englober ses deux soleils à la fois. Ce type d'orbite n'est stable que si la distance qui sépare la planète de ses soleils est au moins quatre fois plus grande que celle qui sépare les étoiles. Du point de vue de la planète, tout se passe comme si les étoiles ne faisaient qu'une. Peut-on estimer le rayon de l'orbite de Tatooine ? Oui, bien sûr ! (…) Remarquons d'abord que les deux étoiles sont assez semblables à notre Soleil : l'une est jaune et l'autre est orange, laissant supposer qu'elle est un peu plus froide. Si ces deux étoiles étaient trop proches l'une de l'autre, elles devraient être déformées par leur gravité mutuelle. Comme aucune déformation n'est perceptible dans la scène du coucher des soleils, on peut calculer que leur distance est légèrement supérieure à 10 millions de kilomètres. Pour avoir une orbite stable Tatooine doit donc être distante de ces deux étoiles d'au moins 40 millions de kilomètres. En fait, elle ne doit pas être si près, sous peine d'être vraiment trop chaude et totalement inhabitable. Deux cent millions de kilomètres est une bonne position : à cette distance Tatooine reçoit une énergie lumineuse un peu supérieure à celle qui frappe la Terre, ce qui expliquerait son aspect désertique. D’après Carte blanche à Roland Lehoucq, astrophysicien, http://www.knowtex.com/nav/les-secrets-de-star-wars_26418. 1. Les étoiles Tatoo 1 et Tatoo 2. 1.1. En supposant que Tatoo 1 et Tatoo 2 ne sont pas déformées et sont à égale distance de Tatooine, montrer, en s’appuyant sur la photo et sur le texte, que la valeur du rayon de chacune des deux étoiles est environ égale à deux millions de kilomètres. Justifier avec soin la démarche utilisée. D'après la photo : dialmètre d'une étoile : 2 r = 6 mm ; distance des centres des deux étoiles : d =19 mm. D'après le texte d est voisin de 10 millions de km ( 1,0 107 km). Par suite 2r = 6 / 19 *1,0 107 = 3,2 106 km ; r ~1,6 106 km. On adoptera pour la suite de l’exercice cette valeur commune pour le rayon des deux étoiles. 1.2. En supposant que les deux étoiles ont la même masse volumique moyenne que le Soleil, évaluer l’ordre de grandeur de la masse MTatoo de Tatoo (1 ou 2). Commenter le résultat obtenu. Volume du soleil : VS = 4 /3 p Rs3 ; masse du soleil Ms. Masse volumique du soleil Ms / VS = 3Ms /( p Rs3 ). Masse volumique de Tatoo MTatoo / VTatoo = 3MTatoo /( p RTatoo3 ). 3Ms /( p Rs3 ) =  3MTatoo /( p RTatoo3 ). Ms /( Rs3 ) =  MTatoo /(  RTatoo3 ).   MTatoo  = Ms( RTatoo/ Rs )3 =2,0 1030 (2,0 / 0,7)3 ~4,7 1031 kg. Tatoo a une masse 20 fois plus grande que le soleil. 2. Tatooine en orbite. Du point de vue de Tatooine, tout se passe comme si les étoiles ne faisaient qu'une, l’étoile unique équivalente sera appelée Tatoo 1-2 ; sa masse sera prise égale à 9,5 × 1031 kg. 2.1. Justifier la phrase précédente à l’aide d’informations données dans le texte. "Du point de vue de la planète, tout se passe comme si les étoiles ne faisaient qu'une." Pour obtenir la masse de Tatoo 1-2, il est cohérent d'ajouter la masse de chaque étoile. Les étoiles ont la même masse, d'où : 2*4,7 1031 ~ 9,5 1031 kg. 2.2. Faire un schéma du système Tatooine-Tatoo 1-2 et représenter sans souci d’échelle la force d’attraction gravitationnelle exercée par Tatoo 1-2 sur Tatooine ainsi que le vecteur accélération de la planète Tatooine dans le référentiel lié à Tatoo 1-2 considéré comme galiléen. 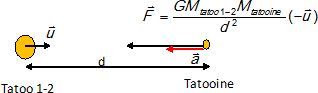2.3. Montrer que le mouvement, supposé circulaire, de la planète dans ce référentiel est uniforme. Le mouvement étant circulaire, la vitesse est portée par la tangente à la trajectoire et la force attractive exercée par Tatoo 1-2 est portée par le rayon du cercle. Force et vitesse étant perpendiculaires à chaque instant, le travail de la force est nul. En conséquence l'énergie cinétique de Tatooine ne varie pas. La valeur de la vitesse de Tatooine reste constante. Le mouvement est donc uniforme. 2.4. Déduire des résultats précédents et du texte, la valeur de la période de révolution de Tatooine. Comparer cette valeur à la période de révolution de la Terre autour du Soleil. 3ème loi de Kepler : T2 / d3  = 4 p2 / (GMtatoo 1-2) avec d = 2,0 1011 m d'après le texte. T2   = 4 p2 d3/ (GMtatoo 1-2) = 4*3,142 *(2,0 1011)3 / (6,67 10-11 *9,5 1031)=4,98 1013  ;  T =7,1 106 s ou 82 jours terrestres. ( environ 0,22 année terrestre ). .

menu