Les Lidar. Bac S Asie 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Les Lidar sont des systèmes de mesure à distance utilisant les propriétés du laser. 1. Lidar topographique embarqué. 1.1. Donner deux propriétés caractéristiques du rayonnement émis par un laser. Faisceau pratiquement monochromatique, très peu divergent, transportant une grande puissance par unité de surface 1.2 A quoi servent les lampes flash lors du fonctionnement du laser ? Les lampes flash réalisent un pompage optique. 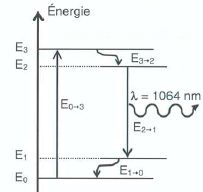1.3. Le niveau fondamental E0 est pris pour origine des énergies. L'énergie du niveau E3 est égale à 2,458 10-19 J. Quelle longueur d'onde doit être présente dans le spectre de la lampe flash ? l = hc / E3 = 6,62 10-34 *3,00 108 /(2,458 10-19) =8,08 10-7 m = 808 nm. Sur la figure ci-dessous, l'avion embarquant le lidar topographique vole à une altitude H = 3,50 km à la vitesse de 450 km /h. Sa position est déterminée par un GPS. 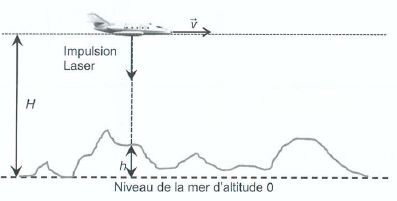1.4. En faisant l'hypothèse que la distance parcourue par l'avion pendant la durée Dt est négligeable par rapport à H, montrer que la durée Dt du trajet aller-retour de l'impulsion laser est :  Dt = 2(H-h) / c. Distance entre le sommet survolé de la montagne et l'avion : H-h ;  distance aller-retour de l'impulsion : 2(H-h) ; célérité de l'impulsion c ;  par suite Dt = 2(H-h) / c. 1.5 Parmi les deux graphiques ci-dessous, indiquer celui qui correspond à la situation étudiée en justifiant. 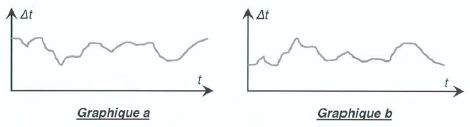Graphe a : Dt est d'autant plus petit que la montagne est plus élevée. 1.6. Lors du survol du Puy de Dôme, on mesure Dt = 13,6 µs. Estimer l'altitude de ce volcan. H-h = ½c Dt ; h = H-½c Dt = 3,50 103 -0,5 *3,00 108 *13,6 10-6=1,46 103 m. 1.7. Dans le cas de la mesure de l'altitude du Puy de Dôme, l'hypothèse faite  à la question 1.4 est-elle vérifiée ? Vitesse de l'avion : v = 450 /3,6 =125 m/s. Distance parcourue en 13,6 µs par l'avion : 125*13,6 10-6 =1,7 10-3 m, valeur très inférieure à H. L'hypothèse est bien vérifiée.. 2. Lidar bathymétrique. Constitués d'un laser infrarouge et d'un laser vert, ils servent à déterminer la profondeur de l'eau. Le rayonnement infrarouge sert à repérer la surface de l'eau. le rayonnement laser vert pénètre dans l'eau et est réfléchi par le fond. 2.1. Les longueurs d'onde des deux lasers sont de 532 nm et de 1064 nm. Attribuer, en justifiant, la longueur d'onde de chaque laser. 532 nm appartient au domaine visible [ 400 ; 800 nm ] et correspond au vert. 1064 nm appartient au domaine infrarouge. 2.2 Expliquer pourquoi il est plus judicieux d'utiliser le laser vert, plutôt que le laser infrarouge pour détecter le fond de l'eau. 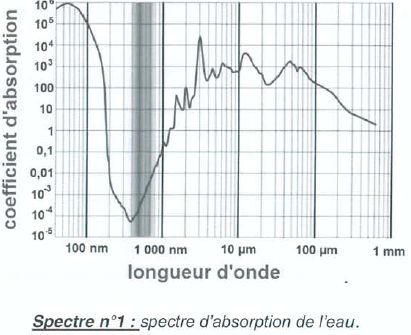L'eau absorbe peu le vert ( coefficient d'absorption 10-4 ) et environ 100 fois plus l'infrarouge ( coefficient d'absorption ~0,01 ). 2.3 Estimer la profondeur de l'eau. 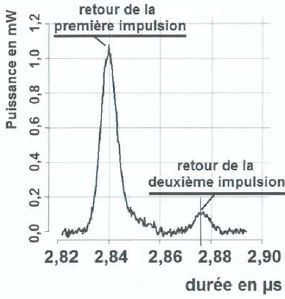Différence du temps de parcours des deux impulsions : Dt = 2,875-2,84 =3,5 10-2 µs. Célérité de la lumière dans l'eau c = 2,26 108 m/s. Profondeur de la mer : 0,5 *2,26 108 *3,55 10-8  ~4,0 m. 3. Le Lidar à effet Doppler. Il permet de faire la mesure des vents où de nuages. Dispositif expérimental : le lidar est remplacé par un ensemble émetteur récepteur à ultrasons et le nuage est modélisé par une plaque fixée sur le chariot. 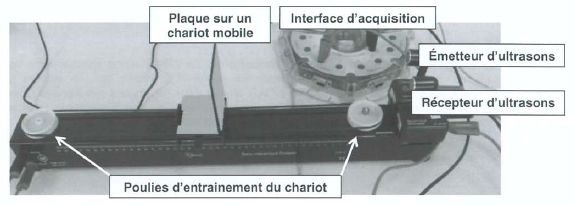Expérience 1 : détermination de la vitesse de déplacement du chariot. On mesure la durée mise par le chariot pour parcourir une distance d = 30,0 ±0,5 cm. Durée moyenne : t = 2,08 ±0,02 s. Expérience 2 : détermination de la vitesse du chariot  à l'aide de l'effet Doppler. Mesure de la fréquence reçue par le récepteur : Chariot immobile f1 = 42170 Hz ; chariot en mouvement f2 = 42134 Hz. Df =  2 v fémise / c avec c = 3,40 102 m/s. 3.1 Citer une différence entre les ondes utilisée par un lidar et celles utilisée dans les expériences. Le lidar utilise des ondes électromagnétiques qui se propagent dans le vide. Dans les expériences, les ultrasons sont des ondes mécaniques, qui nécessitent un milieu de propagation. 3.2. Dans le cas de l'expérience n°1, déterminer la valeur de la vitesse de déplacement du chariot, notée vexp1 et exprimer le résultate en prenant en compte l'incertitude associée. vitesse moyenne : 30,0 / 2,08 =14,4 cm/s Incertitude relative sur la vitesse U(v) / v = [ (0,02 / 2,08)2 +(0,5 /30,0)2]½ =0,02 ; U(v) = 0,02 *14,4 ~0,3 cm/s. Par suite v = 14,4 ± 0,3 cm/s. 3.3.  Dans l'expérience 2, le chariot se rapproche-t-il ou s'éloigne-t-il de l'ensemble émetteur-récepteur ? Justifier. f2 < f1, le chariot s'éloigne de l'ensemble  émeteur -récepteur. 3.4. L'incertitude relative sur la valeur de la vitesse déterminée dans l'expérience 2 est de 5 %. Les deux expériences donnent-elles des valeurs de vitesses compatibles ? v = Df c / (2 fémise) = 36*340 / (2*42170)~0,145 m/s = 14,5 cm/s.. U(v) / v = 0,05 ; U(v) = 0,05 *14,5 = 0,73 ~0,8 cm/s. v = 14,5 ±0,8 cm/s. Les deux expériences donnent des vitesses compatibles, les intervalles de valeurs se recoupent. .

menu