Les acteurs de la
mission Rosetta.
Bas S Antilles 09/2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
La trajectoire de la comète et l'atterrissage de Philaé.
On suppose que la comète parcourt une trajectoire elliptique autour du Soleil.
1.1. En utilisant l'une des lois de Kepler, préciser la position du Soleil représentée sur le schéma ci-dessous.
D'après la première loi de Kepler, le Soleil est l'un des foyers de l'ellipse.
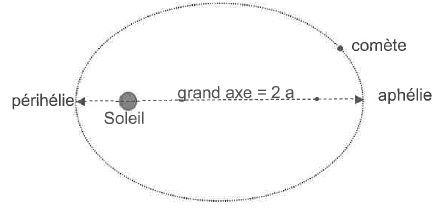
1.2. Quel est la valeur du demi-grand axe a de l'ellipse de la trajectoire de la comète Tchouri ?
Son orbite est elliptique et l'amène à 187 millions de km du Soleil au plus près et 851 millions de km du Soleil au plus loin.
a = ½( 187 + 851) =519 millions de km ou 5,19 1011 m.
1.3.
Enoncer la seconde loi de Kepler.
L'aire balayée par le segment [SM] entre deux positions C et D est
égale à l'aire balayée par ce segment entre deux positions E et F si la
durée séparant les positions C et D est égale à la durée séparant
les positions E et F.
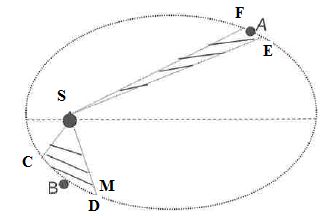
1.4. La vitesse de la comète est-elle plus grande en A ou en B ? Justifier.
CD et EF sont parcourus pendant la même durée. CD est supérieur à EF ; La vitesse est donc plus grande en B qu'en A.
2. La troisième loi de kepler a pour expression T2/a3 = 4p2 / (GM).
a : demi-grand axe de l'ellipse ; M : masse du Soleil ; T période de révolution de la comète.
Retrouver la valeur de la période de révolution de la commète autour du Soleil.
T = [4p2 / (GM) a3]½ = [4*3,142 /(6,67 10-11 *2,00 1030) *(5,19 1011)3]½ =2,03 108 s.
soit environ 6,45 ans.
3.
On s'interesse maintenant à l'atterrisseur Philaé qui est posé sur la
comète. On assimile la comète à une sphère de rayon 2,5 km.
|
|
|
3.1.
Donner l'expression de la force gravitationnelle exercée par la comète
sur Philaé, quand l'atterrisseur est à la surface de la comète.
F = G M m / r2.
M : masse de la comète ; m : masse de l'atterrisseur ; r : rayon de la comète.
3.2. En supposant que cette force est égale au poids de Philaé sur la comète, déterminer la valeur de l'intensité de pesnateur gc sur la comète. ( m =100 kg ; M = 10 milliards de tonnes soit 10 1012 kg )
gc = G M / r2 = 6,67 10-11 * 10 1012* / (2,5 103)2 =1,07 10-4 ~1,1 10-4 m s-2.
3.3. Expliquer et apporter une correction scientifique à la phrase " Philaé pèse 100 kg sur terre et 1 g sur la comète"
Le poids de Philaé est d'environ 1000 N sur terre et 0,1 N à la surface de la comète.
4. En faisant
l'hypothèse que la vitesse de Philaé reste constante au cours de sa
descente sur la comète, estimer la valeur de la phase d'atterrissage de
philaé.
Distance parcourue 20 km ( 2,0 104 m) à la vitesse de 3,5 km / h soit 3,5 / 3,6 = 0,97 m/s.
Durée : 2,0 104 / 0,97 = 2,04 104 s soit environ 5,7 heures.
|
|
|
|
Communication entre Rosetta et la Terre..
Les
communications se font par transmission de signaux. La fréquence
d'émission du signal étudié dans cet exercice est f = 8,4 GHz. Son
débit de transmission est compris entre 5 et 20 kilobits par seconde.
La station construite pour communiquer avec Rosetta, n'est visible que
12 h par jour pour la sonde. Durant la période où le signal ne peut pas
être reçu, Rosetta stocke les données recueillies dans une mémoire de
masse de 25 Go, puis les retransmet lorsque la fenètre de communication
le permet.
Voici une photographie en noir et blanc de la surface de la comète,
prise le 22 août 2014 par le système d'imagerie NavCam de Rosetta,
lorsque la sonde est située à 64,5 km du centre de la comète. Cette
image représente un carré de 7,4 km de côté et possède une définition
de 1024 x 1024 pixels, chaque pixel étant codé par un octet.

1. Quelle est la nature du signal transmis entre la sonde et la Terre ?
Seules les ondes électromagnétiques se propagent dans le vide.
2. La durée
nécessaire pour recevoir les données de Rosetta sur terre est-elle en
accord avec la position de Rosetta par rapport à la terre au moment de
l'atterrissage ?
La distance entre la Terre et la sonde au moment de l'atterrisage est de 510 millions de km, soit 5,1 1011 m.
Durée pour recevoir les données : 5,1 1011 / (3,00 108) =1,70 103 s ou environ 28 minutes. ( donc accord).
3. Est-il possible de distinguer un détail de 1 m sur la comète à partir de la photographie ?
Non, 7400 m correspondent à 1024 pixels soit 7,2 m correpondent à un pixel.
Le noyau de la comète mesure environ 4,1 x 5,4 km.
4. Cette photographie permet-elle de rerouver les dimensions de la comête ?
Oui, voir schéma ci-dessus.
5. Quelle est la taille numérique TN ( en kilooctets de cette photographie ?
TN =1024 * 1024 = 1,05 106 octets ou 1,05 103 ko.
6. Lorsque le débit de transmission est Dt = 12 kilobits par seconde, quelle est la durée le la transmission de cette photographie ?
1,05 103 kilooctets représentent 8 * 1,05 103 ~8,4 103 kilobits.
Dt = 8,4 103 / 12 ~ 7,0 102 s ou 11 min 40 s.
7. Combien de photographies prises par NavCam, la mémoire de masse peut-elle stocker ?
Taille de la mémoire de masse : 25 Go = 25 109 octets.
Taille d'une image : 1,05 106 octets.
Nombre d'images stockées : 25 109 / (1,05 106) ~2,4 104.
|
|