Mathématiques.
Concours Aspts Sud Ouest 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
1. Quelles sont les paires qui
comportent des nombres premiers entre eux ?
78 et 51 ont 1 et
3 comme diviseur commun.
78 = 2*3*13 ; 51 = 3*17.
21 et 40 sont premiers entre eux ( 1 est le seul diviseur commun
).
21 = 3*7 ; 40 = 2*2*2*5.
50 et 11 sont premiers entre eux ( 1 est le seul diviseur
commun ).
50 = 2*5*5.
36 et 44 ont1, 2, 4 comme diviseur commun.
36 = 2*2*3*3 ; 44 = 2*2*11.
2. Calculer sous
forme de fraction, l'expression :
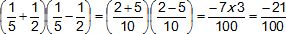
3. L'expression (3x+5)2
-(2x+3)2 est égale à :
Différence de deux carrés :(3x+5+2x+3)(3x+5-2x-3)=(5x+8)(x-2).
ou en effectuant : 9x2+25+30x-(4x2+9+12x)=5x2+18x+16.
4. Quels sont les
nombres qui sont solutions de l'inéquation suivante ?
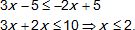
5.
Un sac contient 4 boules vertes numérotées 1, 2, 2, 3 et 2 boules
jaunes numérotées 1, 2. On tire au hasard une boule, la probabilité
d'avoir :
- une boule jaune est 0,5. Faux.
2 succés sur 6 possibilités soit 2/6 = 1/3 ~ 0,33.
- une boule numérotée 2 est de 0,5. Vrai.
3 succès sur 6 possibilités. 3/6 = 1/2.
- une boule verte est de 2 / 3. Faux.
4 succès sur 6 possibilités. 4/6 = 2/3 ~0,66.
- une boule numérotée 1 est de 1/3. Vrai.
2 succés sur 6 possibilités : 2/6 = 1 /3.
6. Le volume d'une
sphère de diamètre 6 cm est, au cm3 près, égal à :
V = 4 /3 p R3
= 4 / 3 *3,14 *33=113 cm3.
|
| .
. |
|
|
7. Une échelle de longueur 2,30 m est
appuyée contre un mur vertical. Le
haut de l'échelle se trouve à 2 m du sol. Calculer la distance entre le
mur et le pied de l'échelle.
Phytagore : 2,32 = 22 +x2 ; x2 =5,29-4 = 1,29 ; x = 1,14 m
~1,1 m ~ 11 dm.
8. Quels sont les nombres qui ne
sont pas égaux à 210 ?
26 x24 = 26+4 = 210.
(25)5 = 225.
0,510 x410=(0,5 x4)10 = 210.
212 / 23 = 212-3 = 29.
9.
L'équation (6x-3)(-3x+2) =0 a pour solutions :
6x-3 = 0 ; 6x = 3 ; x=1/2 =3 / 6; et -3x+2=0 ; 3x=-2 ; x = -2/3.
10.
On donne f---> 4x-3. Cette fonction est :
- affine. Vrai.
- linéaire. Faux.
- sa représentation graphique est une droite. Vrai.
- le coefficient directeur de la représentation graphique est -3. Faux
( coef. directeur = 4).
11. Au cours du
second trimestre, un élève a obtenu la série de notes suivante :
3 ; 10,5 ; 12 ; 13 ; 11 ; 11,5 ; 15 ; 7 ; 9 ; 10 ; 11 ; 13.
Mettre en ordre croissant : 3 ; 7 ; 9 ;10 ; 10,5 ; 11 ; 11 ; 11,5
; 12 ; 13 ; 13 ; 15.
- La médiane de cette série est 11. Vrai.
- 25 % des notes sont inférieures à 10. Vrai ( 3 notes sur 12 : 3/12 =
1/4).
- La moyenne de cette série est 11. Faux ( 10,5).
- L'étendue de cette série est 10. faux.( 15-3 = 12).
12. Donner en
écriture scientifique, le produit de 2,56 10-6 par la somme
de 8,5 102 et 4,7 103.
Somme : 8,5 102 + 4,7 103=5,55 103
puis 2,56 10-6 *5,55 103 = 1,4208 10-2.
|
|
|
|
13. Un triangle ABC est rectangle en
B. On donne AB = 6 et BC = 8.
Un point M est sur [AB) tel que BM = 2,1 et on trace la droite passant
par M et parallèle à (AC). Elle coupe [BC] en un point N. On a alors :
BN = 2,1 ;
MN = 3,5 ; BN = 2,8 ; AC = 10.
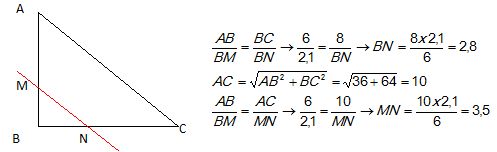
14. Si x
représente le prix en euros d'un article et y le prix du même article
après augmentation ou réduction, on a :
y = 0,95 x correspond à une baisse de 5 %. Vrai.
y = 0,89 x correspond à une augmentation de 11 %. Faux. ( baisse de 11
%).
y= 2x correspond à une augmentation de 100 %. Vrai.
y = 0,05 x correspond à une baisse de 50 %. Faux ( baisse de 95 % ).
15. On
part d'une figure et on veut la réduire en divisant toutes les
dimensions par 4.
Son aire est divisée par 4. Faux ( l'aire est divisée par 16).
Son périmètre est divisé par 4. Vrai.
Son aire est divisée par 8. Faux.
Son aire est divisée par 16. Vrai.
16.
A
la terrasse d'un café, on entend le serbeur annoncer " un chocolat et
un thé : 5,50 € " puis un eu plus tard " quatre chocolats et 2 thés :
17 €. Calculer le prix d'un thé.
Soit x le prix d'un chocolat et y celui d'un thé : x+y = 5,5 soit
x=5,5-y.
4x+2y = 17 soit 4(5,5-y)+2y=17 ; 22-2y=17 ; y = 2,50 €.
17.
L'échelle d'un camion de pompier mesure 32 m. Pour atteindre le dernier
étage d'un immeuble situé à 25 m de hauteur, la mesure de l'angle formé
par l'échelle avec l'horizontale est au degré près :
sin a = côté
opposé / hypoténuse = 25 / 32 =0,781 ; a ~ 51°.
18. Une statue en
marbre pèse 1300 kg. Un artiste fait une maquette de cette statue
à l'échelle 1 / 20. Masse volumique du marbre 2,6 g /cm3.
Quel est le volume de la maquette ?
2,6 g cm-3 = 2600 kg m-3.
Volume de la statue : 1300 / 2600 = 0,5 m3= 5 105
cm3.
Echelle 0,05.
Volume de la maquette 5 105 * 0,053 = 62,5
cm
19. Marc a 108
billes rouges et 135 billes noires. Il les répartit en paquets
identiques contenant des billes des deux couleurs. Toutes les billes
sont utilisées et le nombre de paquets est maximal. Il obtient :
108 = 22*33 ; 135 = 33*5.
Le plus grand diviseur commun de 135 et 108 est 27.
108 * 27*4 et 135 = 27*5.
27 paquets contenant 4 billes rouges et 5 billes noires.
20. Une voiture
roule à vitesse constante de 85 km/h. Quelle distance parcourt-elle en
2 h 36 min ?
36 min ou 36 /60 = 0,6 heure.
85*2,6 = 221 km.
|
|
|
|