Interférences,
balancier d'une horloge.
Concours Orthoptie Tours 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Interférences.
On
veut vérifier la longueur d'onde de la lumière émise par une lampe à
vapeur de mercure en réalisant une figure d'interférences. Les franges
d'interférences sont réalisées avec un système de deux fentes fines
parallèles distantes de a = (0,800 ±0,005) mm. La demi-ouverture de la
tache centrale de diffraction est q = 4,0°. L'écran est placé à D = 1,00 m des fentes. D est mesurée avec une incertitude U(D) = 0,01 m.
Pourquoi les fentes d'Young doivent-elles être très fines ?
Des fentes fines diffractent la lumière.
A quelle condition peut-on avoir des interférences constructives ?
La différence de marche doit être égale à un multiple de la longueur d'onde de la lumière.
On trouve un interfrange i = (0,74 ±0,01 ) mm. Sachant que i = lD/a, calculer l.
l=i a / D = 0,74 10-3 *0,800 10-3 / 1,00 =5,92 10-7 m.
L'incertitude sur la mesure de l peut être évaluée par :
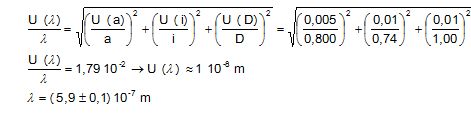
Le constructeur annonçait une longueur d'onde de 589,5 nm. Les résultats de l'expérience encadrent bien cette valeur.
Calculer le nombre de franges brillantes présentes sur l'écran dans la tâche centrale de diffraction.
q= ½L / D ; L = 2q / D avec q = 4*3,14 / 180 =0,0698 rad ;
L = 2*0,0698 / 1,00 =0,1396 m ~140 mm.
L / i = 140 / 0,74 ~189 ; ajoutons la tache centrale brillante, soit 190 franges brillantes.
Sans modifier les fentes, comment pourrait-on augmenter la distance entre les franges ?.
i = lD/a : en gardant a constant, faire croître l'interfrange c'est augmenter D ou / et la longueur d'onde de la lumière.
|
| .
. |
|
|
Balancier d'horloge.
Le
balancier d'horloge dite "horloge de parquet" est un oscillateur
vertical ; il est donc assimilable à un pendule. Pour une faible
amplitude a, la période T de ce pendule vérifie la relation
T = T0(1+a2/16) avec T0 = 2p(L/g)½ où L est la longueur du pendule et a l'amplitude des oscillations en radian.
Montrer par analyse dimensionnelle que (L/g)½ est homogène à une durée.
g est une accélération, soit une longueur divisée par le carré d'un temps.
[g]= L T -2 ; [L/g] = T 2 ; [(L/g)½] = T.
|
.
|
|
Une élévation de température provoque une dilatation de ce balancier de 3 mm. Que devient qualitativement la période ?
Si la longueur du pendule augmente, la période croît.
Quel écart relatif par rapport à T0 est observé sur la période de ce pendule lorsque l'amplitude est de 4 ° ?
4° = 4*3,14/180 rad = 0,0698 rad.
( T-T0)/ T0 = a2/16 = 0,06982/16 = 3,0 10-4.
Une horloge à balancier a une période T1 = 2,000 s en un lieu où g = 9,810 m s-2. Quelle est la période T2 d'une horloge identique en un lieu où g = 9,800 m s-2 en conservant la même amplitude ?
T1 / T2=(g2/g1)½ ; T2=T1(g1/g2)½=2,000 (9,810 /9,800)½=2,001 s.
|
|
|