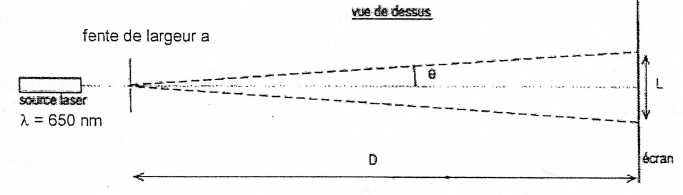
Les fentes d'Young. Concours Orthoptie Montpellier 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . On s'intéresse à deux fentes d'Young F1 et F2, parallèles à un axe Oy, chacune de largeur a = 70 µm, éclairées par une source monochromatique rouge de longueur d'onde dans le vide l = 650 nm. Les deux fentes sont placées sur l'axe Ox et séparées d'une distance b. le plan d'observation est le plan z = D = 1,20 m, distance des fentes à l'écran. Un point d'observation M de l'écran a pour coordonnées (x, y, D). On donne une photographie des interférences visualisées sur l'écran ; on compte 7 franges brillantes à l'intérieur de la tache centrale brillante. L'une des fentes est ocultée. Pourquoi observe-t-on une tache principale sur l'écran ? On observe une figure de diffraction provoquée par l'unique fente dont la largeur est de l'ordre de grandeur de la longueur d'onde de la lumière rouge. Calculer la largeur de cette tache lumineuse. L = 2 l D /  a = 2*650 10-9 *1,20 / (70 10-6)=2,23 10-2 m ~ 2,2 cm. 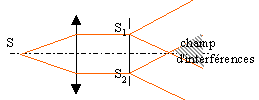Les deux fentes sont ouvertes avec un laser rouge. Faire un schéma des deux faisceaux émergents et hachurer la zone dans laquelle on observe les interférences. Pourquoi les ondes peuvent-elles interférer constructiement ou destructivement ? Les ondes qui interfèrent en un point M ont parcouru des chemins optiques différents. Si cette différence de marche est proportionnelle à la longueur d'onde de la lumière, les ondes qui se superposent sont en phase et les interférences sont constructives. Si cette différence de marche est proportionnelle à un multiple impair de la demi-longueur d'onde, les ondes sont en opposition de phase et les interférences snt destructives. A partir  de la figure d'interférence ci-dessus obtenue sur l'écran, montrer que b ~0,25 mm. 7 franges brillantes correspondent à 6 interfranges sur une longueur d'environ 2 cm. 6 i = 2 ; i = 2 / 6 ~0,3 cm. i = lD / b ; b = lD / i = 650 10-9 *1,20 / (3 10-3)=2,5 10-4 m = 0,25 mm. Quelle est la nature de la frange observée au point d'abscisse x = 18,7 mm ? Différence de marche d = b x / D = 2,5 10-4 *1,87 10-2 / 1,2 ~3,9 10-6 m Ordre d'interférences en ce point d / l = 3,9 10-6 /(650 10-9)~6, valeur entière. Les interférences sont donc constructives. . . Les deux fentes sont ouvertes avec un laser rouge. On change de source monochromatique ( le montage étant inchangé ) ; on passe d'un laser rouge à un laser vert. Indiquer si les grandeurs suivantes sont plus grande, plus petites ou identiques. L'interfrange  est proportionnel à la longueur d'onde de la lumière laser. l vert < l rouge : l'interfrange sera plus petit. La largeur de la figure d'interférences :  la largeur de la tache centrale de diffraction est proportionnelle à la longueur d'onde de la lumière laser. La largeur de cette tache sera plus petite.  Le champ d'interférences ne dépend que de la distance des deux fentes et de la position de l'écran : la largeur de la figure d'interférences reste inchangée. . . .

menu