Pendule: étude dans le champ de pesanteur et dans un champ électrique uniforme. Concours Orthoptie Montpellier 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . Pendule. On considère un pendule simple constitué d'une bille de masse m fixée à un fil inextensible, de longueur L et de masse négligeable. On néglige les frottements. m = 25 g ; L = 1,2 cm ; g = 9,81 m s-2. Etude dans un champ de pesanteur uniforme. On écarte le pendule de sa position d'équilibre d'un angle a0. A un instant t, on lâche la bille sans vitesse initiale. A partir d'une étude énergétique, déterminer l'expression de la vitesse véq de la bille lorsquelle passe par sa position d'équilibre en fonction de L, a0 et g. La position d'équilibre est la référence de l'énergie potentielle de pesanteur. Energie mécanique initiale : Em = mgL(1-cosa0). Energie mécanique au passage àla position d'équilibre : Em =½mv2éq. Conservation de l'énergie mécanique : mgL(1-cosa0)=½mv2éq. v2éq = 2gL(1-cosa0) ; véq = (2gL(1-cosa0))½. . Déterminer la valeur de l'angle a0 pour que labille atteigne une énergie cinétique de 0,4 mJ lors de son passage à la position d'équilibre. mgL(1-cosa0)=4  10-4 ; 1-cosa0=4  10-4 /(mgL) ; cosa0=1-4  10-4 /(mgL). cos a0 =1-4 10-4 /(0,025*9,81 *0,012) =0,864 ; a0 =30,22 ~30°. Rappeler l'expression du travail du poids en fonction de la variation de l'énergie potenteille de la bille. Donner ses caractéristiques durant le trajet de la bille. Le travail du poids est égal à l'opposé de la variation de l'énergie potentielle de la bille.   Premier quart et troisième quart de période : le travail est moteur et vaut 0,4 mJ. Second quart et quatrième quart de période : le travail est résistant et vaut -0,4 mJ. On souhaite déterminer la valeur de la tension T du fil. Donner l'expression de la tension T du fil à un instant t de la trajectoire de la bille en fonction de m, véq, L, q, et g. 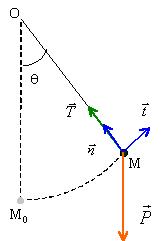Ecrire la seconde loi de newton selon l'axe n : T - mg cos q =mv2/ L. T  = m(v2/ L +g cos q ). Conservation de l'énergie mécanique :  mgL(1-cos q)+½mv2 =½mv2éq. mv2 / L = mv2éq / L- 2mg(1-cos q). T =mv2éq / L-mg(2-3cos q). Calculer T pour q = a0. T =mg cos a0 =0,025*9,81 *0,864 =0,21 N. . . Etude dans un champ électrique uniforme. On remplace la précédente bille par une bille chargée ( 10 nC) de même masse que l'on positionne entre les armatures 1 et 2 d'un condensateur espacées d'une longueur L. Spontanément la bille se déplace vers l'armature 2 en faisant un angle a0 par rapport à la normale. Représenter sur un schéma les forces qui s'exercent sur la bille dan sa position d'équilibre. On représentera également le champ électrique tout en rappelant ses caractéristiques. 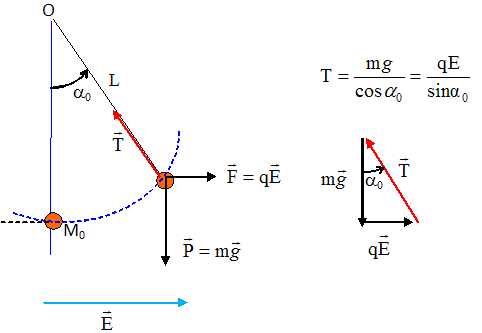Le champ électrique uniforme est perpendiculaire aux armatures, dirigé vers le plus petit potentiel, de valeur constante E = U12 / L. . La tension du fil a-t-elle été modifiée ? Si oui calculer sa nouvelle valeur. T = mg / cos a0 = 0,025*9,81 / cos 30,22 =0,2838 ~0,28 N. Calculer la force électrique exercée sur la bille. F = mg tan a0 = 0,025*9,81 *tan 30,22 =0,1429 ~0,14 N. Calculer la tension électrique entre les armatures. F = qE = q U12 / L ; U12 = F L / q = 0,1429 *0,012 / (10 10-9)=1,7 105 V. .

menu