QCM : Pendule, champs et forces, mouvement. Concours kiné St Michel 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . 15. Position, vitesse, accélération. ( 1 pt). Un mobile se déplace suivant un axe Ox horizontal, orienté positivement de gauche à droite pour les cas A, B et C. Cet axe est vertical orienté vers le bas pour le cas D. 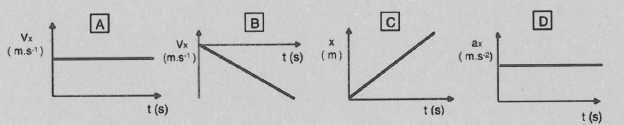- Pour le cas A, la somme des forces exercées sur le mobile se compensent. Vrai. Le mouvement est rectiligne et uniforme. - Pour le cas B, le mobile recule. Vrai. La vitesse est dirigée dans le sens contraire de l'axe. - Pour le cas C, l'accélération est nulle. Vrai. La position est une fonction affine croissante du temps ; la norme de la vitesse est constante. - Le cas D peut correspondre à une chute libre. Vrai. La composante de l'accélération suivant un axe vertical orienté vers le bas est constante. 16. Pendule simple. (1,5 pts) Un pendule simple est constitué d'une bille de petite dimension, de masse m=100 g, reliée à un support fixe par un fil inextensible de longueur L = 90,0 cm et de masse négligeable. On écarte ce pendule de sa position d'éuilibre d'un angle a = 60 ° et on le lâche sans vitesse initiale en A. On choisit le point O comme référence pour l'énergie potentielle de pesanteur. L'énergie mécanique de la balle en O vaut 4,5 10-2 J. 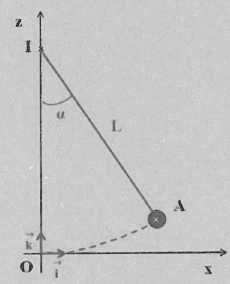- En A, l'expression de l'énergie potentielle de la bille est mgL(1-cos a). Vrai. - Il n'y a pas de frottement. Faux. Energie mécanique en A : mgL(1-cos a) =0,10 *9,81 *0,90(1-cos60) ~0,45 J. Energie mécanique en O : 0,045 J. L'énergie mécanique diminue du travail des frottements. - La  bille arrive en O avec une vitesse de 3,0 m/s. Faux. v = (2Em(O) /m)½ = (2*0,045 /0,10)½=0,95 m/s. - Si on augmente la masse de la bille, l'énergie mécanique augmente mais pas la vitesse en O. Faux. Dans l'hypothèse de la conservation de l'énergie mécanique, la vitesse en O ne dépendrait pas de la masse. . . 17. Champs et forces. (0,5 pt) - Un champ scalaire est caractérisé par un vecteur qui possède une direction, un sens et une norme. Faux. Un scalaire est caractérisé par un nombre. - Une ligne de champ magnétique est une courbe tangente au vecteur champ magnétique en chacun de ses points. Elle rentre par le pôle nord et sort par le pôle sud. Faux Elle rentre par le pôle sud et sort par le pôle nord. - Les lignes de champ électrostatique sont orientées en fonction de la charge créant le champ électrostatique. Pour une charge positive, les lignes de champ partent de la source. Vrai.  - Le champ de gravitation est un champ vectoriel. Vrai. . On se  place dans le référentiel terrestre supposé galiléen. Les frottements de l'air sont négligés. Lors d'une partie de Rugby, un joueur A est animé d'un mouvement rectiligne uniforme. A l'instant t = 0 s, le joueur A, de masse mA = 120 kg, tape dans le ballon, vers le haut, afin que celui-ci passe la ligne de défense adverse. A l'instant t = 10 s, le joueur A qui se déplace à la vitesse vA = 5,0 m/s entre en collision avec le joueur B immobile, de masse mB = 80 kg. L'ensemble des deux joueurs forme un système isolé. Les joueurs et le ballon seront supposés ponctuels. A l'instant t=0, le vecteur vitesse du ballon fait un angle de 60° avec l'axe Ox et sa valeur est v0 = 10,0 m/s. Dans le repère (O, i, j ), l'origine coïncide avec la position initiale du ballon et du joueur A. Le graphe ci-dessous représente la trajectoire du ballon dans le repère choisi. 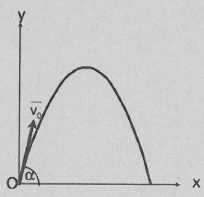18. (1,5 pts). - Le ballon est en chute libre. Vrai. Les frottements de l'air étant négligés, le ballon n'est soumis qu'à son poids. - Les équations horaires de la vitesse du ballon sont vx(t) = v0 sin a et vy(t) = -gt + v0 cos a. Faux. vx(t) = v0 cos a et vy(t) = -gt + v0 sin a. - Le ballon touche le sol à la date t = 1,8 s. Vrai. x= v0 cos a t ; y = -½gt2 +v0 sin a t =0 ; -½gt +v0 sin a  =0 ; t = 2v0 sin a  / g = 2*10 sin 60 / 9,81 ~1,8 s. - Le ballon monte à plus de 3,0 m de haut. Vrai. Au sommet S de la parabole vy=0 : t = v0 sin a / g =10*sin 60 / 9,81 ~0,88 s. yS =-4,9 *0,882 +10 sin 60 *0,88 ~3,8 m. 19.  1,5 pts. - Le graphe représentant la position y du ballon en fonction du temps est une parabole tournée vers le bas.  Vrai. - Pour récupérer le ballon au moment où il touche le sol, le joueur A doit parcourir 9,0 m. Vrai. vA t = 5,0 *1,8 =9,0 m. - Pour récupérer le ballon au moment où il touche le sol, le joueur doit courir avec une vitesse de 5,0 m/s. Vrai. - Après le choc, le système isolé constitué des deux joueurs a une vitesse de 3,0 m/s. Vrai. mA vA = (mA +mB) v ; v = 120*5,0 /(120+80) =3,0 m/s. .

menu