QCM physique
chimie. Concours PACES Lyon 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
14. Polarisation
On considère trois ondes planes électromagnétiques décrites dans repère orthogonal par les champs électriques suivants ( avec E0, w, k et a des constantes).
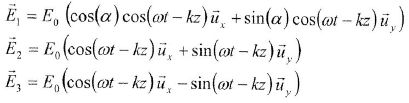
La polarisation est rectiligne pour les ondes :
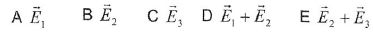
Le champ électrique doit
conserver une direction fixe, dans le plan xOy, au cours du temps. La
forme mathématique du champ électrique est alors :
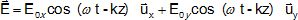 Réponse E. Réponse E.
15. Foyers d'un dioptre sphérique.
On considère un dioptre sphérique de courbure SC = +10 cm séparant deux milieux d'indice de réfraction n1 = 1 et n2 = 1,5. Ses foyers objet F et image F' vérifient :
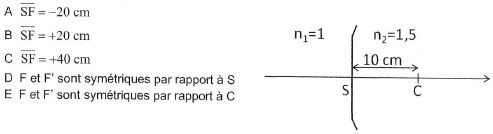
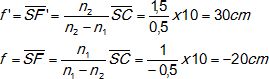 Réponse A. Réponse A.
16. Spectre de vibration du monoxyde de carbone.
Le spectre donne une bande d'absorption à 2140 cm-1. On donne hc / e = 1,24 10-6 SI.
A. L'ordre de grandeur de la longueur d'onde dans cette bande est 4,5 µm. Vrai.
1 / 2140 = 4,7 10-4 cm = 4,7 µm.
B. La fréquence correspondante est de l'ordre de 6,4 1013 Hz. Vrai.
n = c / l =3 108 / (4,7 10-6) = 6,4 1013 Hz.
C. L'énergie de cette transition est d'environ 0,3 eV. Vrai.
E = hc / l ( en joule) ; E = hc /(e l )( en eV)
E = 1,24 10-6 / (4,7 10-6) =0,27 eV.
D. La masse réduite d'une molécule CO vaut environ 7 10-26 kg. Faux.
mC =0,012 / (6 1023) ; mO =0,016 / (6 1023) kg.
masse réduite : µ=mC mO / (mC +mO ) =0,012*0,016 / 0,028*6 1023)=1,1 10-26 kg.
E. Pour obtenir le nombre d'onde de l'absorption correspondant à une molécule 13C16O, il suffit de multiplier celui de 12C16O par ((12*28) / (13*29))½. Faux.
Le nombre d'onde est inversement proportionnel à la racine carrée de la masse réduite.
1/ l12C16O = k / µ½12C16O avec k une constante.
1/ l13C16O = k / µ½12C13O =1/ l12C16O µ½12C16O / µ½12C13O ;
µ½12C16O / µ½12C13O =[12*29 / (13*28)]½.
|
| .
. |
|
|
17. Loi de Biot et Savart.
Un courant I de 10 A passe dans une spire de diamère D = 1 m. Soit B le
champ magnétique qu'elle crée et N le nombre de spires de la bobine. µ0 = 4 p 10-7 SI.
A. Au centre de la spire B = 6,3 mT. Faux.
B = µ0 I / D=4*3,14 10-7 *10 ~1,25 10-5 T.
B. Au centre de la spire B = 12,5 µT. Vrai.
C. Le nombre de spires identiques nécessaire pour obtenir BN = 0,1 T est N = 8000. Vrai.
N = BN / B = 0,1 / (1,25 10-5)= 8000.
D. Le nombre de spires identiques nécessaire pour obtenir BN = 0,1 T est N = 10000. Faux.
E. Le courant Ib1 pour obtenir un champ B1 = 1 T avec N spires vaut 1000 A. Faux.
B = µ0 N I / D ; I = BD / (µ0N) = 1 /(4*3,14 10-7 N) ~ 8 105 / N.
Si N = 8000 alors I = 100 A.
18. Loi de Moseley.
Cette loi l-½ = A(Z-s) donne la relation entre la longueur d'onde l
d'une raie X caractéristique et le numéeo atomique du matériau émeteur.
A et s sont des constantes ( s=1 pour lune raie de la série K).
A. Les constantes A et s sont sans dimension. Faux.
Z et donc s sont sans dimension ; A est l'inverse
de la racine carrée d'une longueur.
B. La valeur de la constante A est identique pour les raies Ka et Kß. Faux.
C. La valeur de la constante d'écran s est plus grande pour les raies La que pour les raies Ka.
Vrai.
L'effet d'écran est petit pour pour la transition Ka et augmente pour les autres couches.
D. Une raie Lß est produite lors d'une transition électronique depuis un niveau M ( n=3) vers un niveau L ( n=2). Faux.
Transition du niveau N vers le niveau L.
E. Le rapport de la longueur d'onde de la raie Ka du zinc ( Z = 30) sur celle du cuivre ( Z = 29) est égal à (28/29)2. Vrai.
l = 1/(A2(Z-s)2) = 1/(A2(Z-1)2)
lZn = 1/(A2(29)2) ; lCu = 1/(A2(28)2) ; lZn / lCu= (28/29)2.
19. Activité.
On dispose d'une masse m = 1,3 pg d'azote 13 radioactif de période T = 10 min .
A. Le nombre de noyaux correspondant à la masse m est 6 1011. Faux.
Masse d'un noyau d'azote 13 : 13 / NA gramme ;
nombre de noyau : 1,3 10-12 / 13 *6 1023 = 6 1010.
B. L'activité initiale correspondant à la masse m est égale à 4,1 GBq. Faux.
l = ln2 / T ; A = l N = 0,69*6 1010 /(10*60) =6,9 107 Bq.
C. L'activité initiale correspondant à la masse m est égale à 69 MBq. Vrai.
D. L'activité initiale correspondant à la masse m est égale à 34,5 MBq après 20 min. Faux.
L'activité initiale est divisée par 4 au bout de deux périodes. 69/4 ~ 17 MBq.
E. L'activité correspondant à la masse m est 64 fois plus faible au bout d'une heure. Vrai.
L'activité initiale est divisée par 26 =64 au bout de 6 périodes.
|
|
|
|
20. Désintégration radioactive.
Le carbone 11 se désintègre en bore 11 par transformation isobarique.
La masse de l'atome de carbone 11 est supérieure de 0,002 u à celle du
bore 11. On donne 1 u = 931,5 MeV / c2.
A. L'énergie maximale des positons émis est 0,841 MeV. Faux.
0,002 *931,5 =1,86 MeV.
B. Au cours de cette transformation, un neutron est transformé en proton. Faux.
116C --->115B + 01e + neutrino soit 11p --->10n + 01e.
C. La désintégration par capture électronique est possible. Faux.
La capture électronique concerne les noyaux riches en protons.
D. A la suite de la transformation radioactive, on peut observer un photon de 0,511 MeV. Vrai.
Le positon instable peut s'annihiler avec un électron du milieu. Il en résulte deux photons d'énergie 0,511 MeV.
E. Le neutrino émis possède un spectre d'énergie continu. Vrai.
De même que le positon.
21. Interféromètre.
Une
source ponctuelle S émet une lumière monochromatique de longueur d'onde
600 nm. L'interféromètre ci-dessous est constitué d'un miroir
semi-réfléchissant ( coefficients de réflexion et de transmission 50 %)
d'épaisseur négligeable et de deux miroirs parfaits M1 et M2
placés dans l'air. Le signal au niveau du point H résulte des
interférences entre les rayons lumineux de même intensité créés à
partir d'un rayon horizontal issu de S. Lorsque d2-d1 =0, l'intensité en H vaut I0. Lorsque d2-d1 = 300 nm, l'intensité en H est I. Le rapport I / I0 vaut : 0 ; 1 / 8 ; 1 / 4 ; 1 / 2 ; 1.
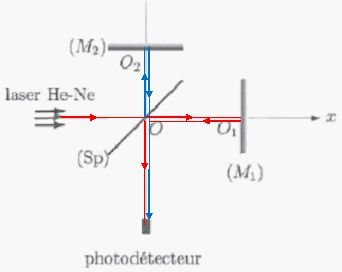 d1 = O2O ; d2 = OO1. d1 = O2O ; d2 = OO1.
d2-d1 =0 : la différence de marche est nulle et les interférences sont constructives.
d2-d1 = 300 nm = ½ l :la différence de marche est un multiple impair de la demi-longueur d'onde et les interférences sont destructives. ( I=0)
I / I0 = 0.
22. Distibution de charges ponctuelles.
Soit
un axe Ox sur lequel sont placées des points A, B, O, C et D de
coordonnées respectives -2a, -a, 0 +a et +2a. Une charge q positive est
placée en A et en C, une charge -q est placée en B et en D. V(O) et
E(O) sont respectivement le potentiel et le champ électrostatiques
créés en O par cette distribution de charges ponctuelles, dans le vide.
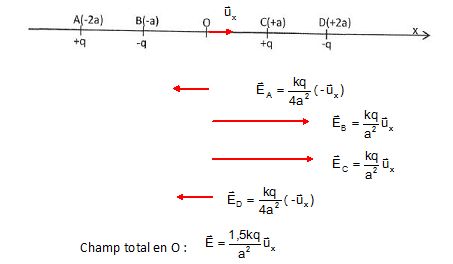
A. V(0)=0. Faux.
B. E(O)=0. Faux.
C. Une charge Q positive placée en O subit une force de même sens que l'axe Ox. Vrai.
D. L'énergie potentielle électrostatique de la charge Q placée en O est nulle. Faux.
E. Un dipôle
électrostatique placé en O, perpendiculairement à l'axe Ox, tourne de
180 ° pour se mettre dans la position d'équilibre stable. Faux.
Il s'oriente dans le champ en tournant d'un angle de 90°.
23. Comparaison d'un laser et d'une ampoule électrique.
On considère deux sources de lumière :
- une ampoule électrique délivrant une puissance lumineuse de 10 W ;
- un laser de longueur d'onde 610 nm délivrant un faisceau de diamètre initial d = 1 cm et d'angle de divergence q = 2 mrad et de puissance lumineuse 0,3 mW.
On considère un écran placé à 10 m de ces sources
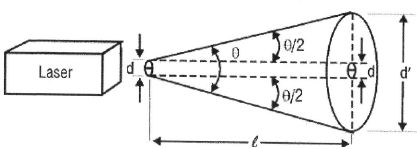
On utilisera les approximations 1 / p ~0,3 et tan q ~q pour les petits angles.
A. L'intensité sur l'écran de la lumière émise par l'ampoule est 75 mW m-2.
L'ampoule éclaire dans toutes les directions de l'espace ; valeur approximative du flux lumineux : 100 lumens.
Intensité sur l'écran : 100 / (4p) ~100 *0,3 / 4 = 7,5 candela.
B. L'intensité sur l'écran de la lumière émise par l'ampoule est 7,5 mW m-2.
C. Le diamètre du faisceau laser sur l'écran est d' = 5 cm. Faux.
tan ( ½q) ~½q =(d'-d) / (2l) ; d'-d =q l =2 10-3 *10 = 2 10-2 m = 2 cm ; d' = 3 cm.
D. L'intensité du faisceau laser au niveau de l'écran est 4 mW m-2. Faux.
Surface de la tache lumineuse sur l'écran p d'2 /4 = p 9 10-4 /4 m2 ;
0,3 10-3 *4/ (9 10-4 p)~0,3*0,3 10 *4/ 9 = 0,4 W m-2 = 400 mW m-2.
E. L'intensité du faisceau laser au niveau de l'écran est 25 mW m-2. Faux.
24. Diffusion Compton.
Un photon d'énergie E subit une diffusion Compton sur un électron de masse m = 0,511 MeV c-2. Le photon est diffusé selon une direction faisant un angle q avec la direction incidente. L'énergie E' du photon diffusé est donné par la relation :
E' = E / [1+E(1-cosq) / (mc2)].
A. Pour E = 0,511 MeV et q = 90°, l'énergie cinétique de l'électron compton est égale à ½E. Vrai.
Lorsqu'un
photon X passe à proximité d'un électron périphérique peu lié à
l'atome, l'énergie du photon est en partie transmise à l'électron : ce
dernier est arraché de l'atome et s'échappe avec une certaine énergie
cinétique. Le reste de l'énergie se retrouve sous la forme d'un photon
X de direction différente et d'énergie inférieure.
E / (mc2 ) = 1 ; E' = ½E ; énergie cinétique de l'électron : E-E' = ½E.
B. Pour E = 1,022 MeV et q = 90°, l'énergie cinétique de l'électron compton est égale à E/3. Faux.
E / (mc2 ) = 2 ; E' = E / 3 ; énergie cinétique de l'électron : E-E' = 2E/3.
C. Pour E = 0,511 MeV et q = 180°, l'énergie cinétique de l'électron compton est égale à 2E/3. Vrai.
E / (mc2 ) = 1 ; cosq= -1 ; E' = E/3 ; énergie cinétique de l'électron : E-E' = 2E/ 3.
D. Pour E = 1,022 MeV et q = 180°, l'énergie du photon diffusé est égale à E/5. Faux.
E / (mc2 ) = 2 ; cosq= -1 ; E' = E / 4.
E. La diffusion Compton se produit préférentiellement avec les électrons atomiques les plus fortement liés. Faux.
25. Ressort.
Une masse m reliée à un ressort de raideur k, de longueur à vide L0 oscille sans frottement le long de l'axe x. Le ressort est lâché à t=0 avec une vitesse v0 et un écartement x0 par rapport à sa position d'équilibre et avec v0 / x0 = 1 s-1.
Pulsation propre du système w0 = 1 rad/s.
La position de la masse à tout instant est décrite par :
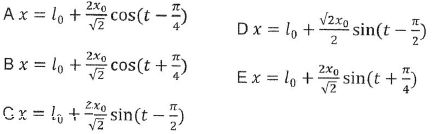
x(t) =L0+ X0 cos (w0t+f).
Conservation de l'énergie : ½mv20 + ½kx20 = ½kX20 ; v0 = x0 et w20 = k/m = 1 soit m = k.
x20 + x20 = X20 ; X0 = 2½x0.
x(t=0) =L0+x0 = L0+ 2½x0 cos (f) ; 1 =2½ cos (f) ; f = ±45° =± p / 4.
|
|