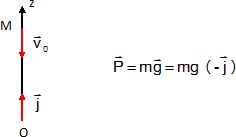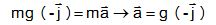QCM chute verticale. Concours ESA Lyon 2014

QCM chute verticale. Concours ESA Lyon 2014, Geipi Polytech 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

.
.

Exercice 3. L'urologue doit quelque fois mettre en place une endoprothèse urètérale : c'est un tube introduit dans l'uretère facilitant le passage des fragments de calculs entre le rein et la vessie. On sinteresse à la chute verticale d'un fragment de masse m du clacul, le long de l'endoprothèse remplie d'urine. Durant la chute le calcul est soumis à son poids et à une force de frottement F_f de norme F_f=kV où V est la vitesse de chute et k une constante. Le graphe ci-dessous retrace l'évolution de la vitesse de chute au cours du temps qui se décompose en deux phases (1) et (2).

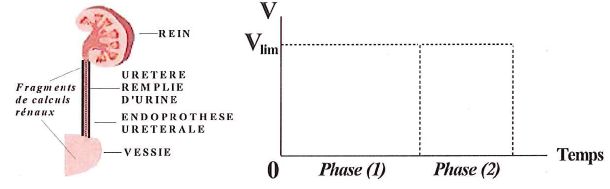
9. Durant la phase (1) le fragment présente un mouvement :
A. Rectiligne et accéléré de façon non uniforme. Vrai.
La force de frottement n'est pas constante : l'accélération ne sera pas constante. La vitesse croît de zéro à une valeur limite.
B. Rectiligne et décéléré de façon non uniforme. Faux.
C. Rectiligne et accéléré de façon uniforme. Faux.
D. Rectiligne et décéléré de façon uniforme. Faux
E. Rectiligne et uniforme. Faux.
La somme vectorielle des forces n'est pas nulle.

10. Parmi les schémas suivants, quel est celui, donnant pour la phase (1) du mouvement de chute, une représentation correcte des vecteurs vitesse et accélération du fragment en chute ?

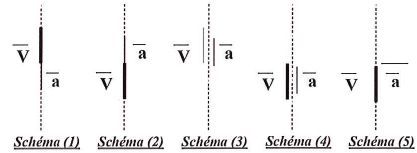
Le vecteur vitesse a toujours le sens du mouvement, donc dirigé vers le bas : ( schéma 1 exclu). La vitesse croît, l'accélération a le sens de la vitesse, donc schéma 4.

11. Durant la phase (1), le fragment de calcul :
A. Voit son énergie mécanique diminuer. Vrai.
L'énergie mécanique diminue du travail des frottements.
B. Voit son énergie mécanique rester constante. Faux.
C. Voit son énergie potentielle de pesanteur diminuer. Vrai.
D. Voit son énergie cinétique augmenter. Vrai.
E. Voit son énergie cinétique varier plus que son énergie potentielle de pesanteur. Faux.

12. Dans l'expression de la force de frottement, l'unité du coefficient k est kg s^-1. Dans la liste des propositions ci-dessous, identifier par analyse dimensionnelle, l'expression de la vitesse limite V_limde chute du fragment.
mg-k ; k / (mg) ; mk /g ; mg / k ; k m g.
[k / (mg)]= M T^-1 M^-1 L^-1T² =L^-1T.
[mk/g]=M M T ^-1 L^-1T² = M²L^-1T.
[mg/k] =M L T ^-2 M^-1 T =L T ^-1. Vrai.

.
.

13. Dans la phase (2), si H est la hauteur de chute parcourue par le fragment à la vitesse V_lim, quelle est l'expression de la force de frottement pour ce déplacement ?
-k V_lim H ( Vrai) ; +kV_lim H ; -k V_lim / H ; + k V_lim/ H ; 0.
Le travail des frottement est résistant ; le travail est le produit scalaire d'une force par un déplacement.

Exercice 4.
Une fois parvenus jusqu'à la vessie les fragments du calcul rénal sont éliminés par la voie urinaire. On s'intéresse à un fragment de masse m expulsé du système urinaire d'une hauteur h avec une vitesse initiale v₀ orientée verticalement vers le bas. Durant sa chute, on suppose qu'il n'est soumis qu'à l'action de son poids.
Quelle est l'expression vectorielle du poids ?

.

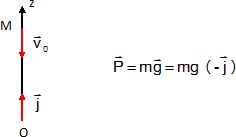
Enoncer la seconde loi de Newton puis donner l'expression mathématique de l'accélération du fragment.
Dans un référentiel galiléen, la somme vectorielle des forces extérieures au système est égale au produit de la masse du système par l'accélération de son centre d'inertie.

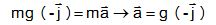
Avec pour origine des temps l'instant d'expulsion et pour origine des positions le point O établir les expressions de la coordonée a_z du vecteur accélération, de la coordonnée v_z du vecteur vitesse, de la coordonnée z du vecteur position.
a_z= -g.
La vitesse est une primitive de l'accélération : v_z = -gt + Cste.
v_z(t=0) = -v₀ = cste ; v_z = -gt - v₀.
La position est une primitive de la vitesse : z = -½gt² +v₀t + cste.
z(t=0) = cste = h ; z = -½gt² -v₀t + h.

Deux étudiants, Sarah et Gaspard, cherchent à déterminer la profondeur du puits d’accès d’une mine. Celui-ci est vertical et suffisamment profond pour que le fond à la profondeur H soit invisible. Gaspard propose de lâcher une pierre dans le puits et de déduire du temps de chute la profondeur du puits.
Il analyse l’expérience en ne tenant compte de la seule pesanteur. Soit t le temps écoulé à partir du moment où la pierre est lâchée à vitesse nulle au-dessus du puits, z(t) la position de la pierre à l’instant t et v(t) sa vitesse.
Données :
Accélération de pesanteur g = 9,81 m.s^-2. Vitesse du son c = 343 m.s^-1.
Masse de la pierre m = 100 grammes. z=H fond du puits ; z=0 surface.
IV-1- En faisant l’hypothèse que seule la force de pesanteur agit sur la pierre et en appliquant la 2^ème loi de Newton, exprimer l’accélération verticale a.
On choisit un axe vertical orienté vers le bas, origine : partie haute du puits. a = g = 9,81 m s^-2.
IV-2- En déduire les expressions de la vitesse v(t) et la position z(t) au cours de la chute.
La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : v(t) = 9,81 t.
La position est une primitive de la vitesse et position initiale est nulle : z(t) = 4,905 t².
Soit t₁ le temps de chute mis par la pierre pour atteindre la profondeur H. On peut exprimer t₁ de la sorte
t₁ = a H^½ avec a=0.452 SI.
IV-3- Donner l’expression littérale de a.
H = ½gt₁² ; t₁ = (2 H / g)^½ ; a =(2 / g)^½.
On mesure la durée t_mes= 19,17 s entre le moment du lâché et le moment où le son de choc est perçue à la surface.
IV-4- Exprimer ce temps en fonction de t₁ et du temps t₂ mis pour que le choc soit perçu, puis exprimer ce temps en fonction de H.
t_mes = t₁ +t₂ = a H^½ + H/ c.
IV-5- On peut reformuler l’équation précédente sous la forme H + ß H^½ +g = 0 = 0 avec ß = 155 SI et g = −6575 SI. Donner les expressions littérales de β et g ainsi que leurs unités.
a H^½ + H/ c +t_min = 0 ; H +a c H^½ + c t_min = 0.
ß = a c ( m^½); g = c t_mes (mètre).
IV-6- Calculer la profondeur H du puits en résolvant numériquement l’équation en H.
H +155 H^½ -6575 =0.
On pose X² = H ; X² +155 X -6575 = 0 ; D =155² + 4 x6575 =50325 ; D^½ =224,33.
On retient la valeur positive X = (-155 +224,33) / 2 = 34,67 ; H = 34,67² ~1200 m.
Sarah estime qu’il faudrait prendre en compte, en plus de la pesanteur, une force de frottement f. En appliquant ses cours de mécaniques des fluides, elle modélise cette force de la manière suivante :
- sa direction est celle du mouvement, - son sens est opposé au mouvement, - sa norme a pour expression f = kv² avec k = 1,190 10⁻³ SI.
IV-7- En appliquant la 2^e loi de Newton, exprimer l’accélération verticale a′ .
mg -kv² = m dv/dt = m a' ; a' = g-k / m v^2..
La vitesse limite v_lim est atteinte par la pierre lorsque l’accélération devient nulle.
IV-8- Exprimer puis calculer v_lim.
mg -kv_lim² =0 ; v_lim = (m g / k)^½=(0,100 x9,81 / (1,190 10^-3)^½=28,7 m / s.
Sarah considère que le mouvement est en fait constitué de deux phases :
- une première de l’instant t= 0 à l’instant T = v_lim / g où la force f ne s’exerce pas,
- une seconde phase pour t supérieur à T où la vitesse est constante et égale à v_lim.
IV-9- Définir le mouvement de la pierre lors la première phase puis lors la seconde phase.
Première phase : mouvement rectiligne uniformément accéléré.
Seconde phase : mouvement rectiligne uniforme.
IV-10- La profondeur atteinte z(t) après une durée de chute t > T est telle que :
z(t) = A T² +B (t-T) avec A = 4.90 SI et B = 28.72 SI. Donner les expressions des coefficients A et B ainsi que leurs unités.
z(t) = ½g T² + v_lim(t-T).
A = 0,5 g ( m s^-2) ; B = v_lim ( m / s).
IV-11- Exprimer l’estimation H'de la profondeur du puits en fonction de la durée mesurée t_mes entre le lâché de la pierre et le bruit de son arrivée. Calculer H'.
t = t_mes-H'/c.
H' = AT² + B(t_mes-H' / c-T) ; H' ( 1+B / c)= AT²+B(t_mes-T) / (1 +B/ c).
H' = [4,90 x(28,7 /9,81)²+ 28,72 (19,17 -28,7 / 9,81)] / (1 +28,72 / 343) =(41,94+466,54) / 1,084 =469 m.

.

menu