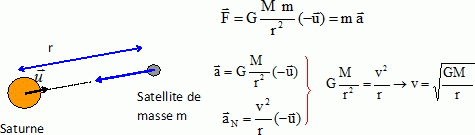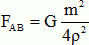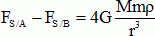Les anneaux de Saturne. Concours Audioprothèsiste Paris 2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . « On pourrait croire que les anneaux de Saturne sont d’un seul tenant. En fait il s’agit de nuées de pierrailles, dispersées tout au long d’un plan équatorial, qui circulent en orbites individuelles autour de la planète » affirmait Hubert Reeves dans un de ses ouvrages, Poussières d’étoiles. Le but de cet exercice est de juger la compatibilité d'un modèle avec la deuxième phrase de cette citation. L’interaction de gravitation : On considère une planète P, de symétrie sphérique, de masse M et un objet assez petit (assimilable à un point matériel) de masse m situé à l’extérieur de la planète. Donner l’expression vectorielle de la force F exercée par la planète sur l’objet. On précisera, sur un schéma, la direction et le sens de cette force ; on définira de façon précise les différents paramètres utilisés pour l’exprimer. 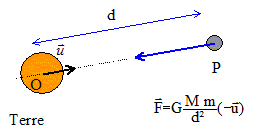M : masse de la planète ( kg) ; m : masse du satellite ( kg) ; d : distance du centre de la planète au satellite en mètre; G constante de gravitation ; u : vecteur unitaire. Satellite gravitant sur une orbite circulaire : Dans l'étude d’un satellite terrestre, on utilise le référentiel géocentrique. Dans le cas présent, quel référentiel analogue doit-on choisir ? Préciser ses caractéristiques. Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes. Le référentiel saturnocentrique a pour origine le centre de Sarurne et des axes parallèles à ceux du référentiel héliocentrique. Un objet ponctuel gravite sur une orbite circulaire, de rayon r, soumis uniquement à l'attraction gravitationnelle de la planète P. Montrer que la valeur de la vitesse v de l'objet reste constante et exprimer cette vitesse en fonction de r et des paramètres définis précédemment. 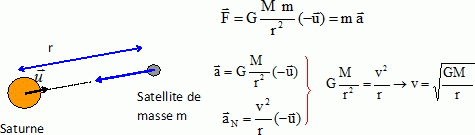Le satellite n'est soumis qu'à la seule force de gravitation. Cette force étant perpendiculaire à la vitesse, ne travaille pas. L'énergie cinétiquedu satellite  n'est pas modifiée : la avleur de la vitesse reste constante. Définir la période de révolution T et donner son expression avec les mêmes paramètres que la vitesse v. Montrer qu'on retrouve ainsi la troisième loi de Kepler. Préciser, dans la situation présente, l’expression de la constante utilisée dans cette loi. La période est la durée nécessaire pour parcourir la circonférence 2 p r à la vitesse v. 2 p r  = v T ; 4 p2 r2 = v2 T2  = GM / r T2 ; T2  = 4 p2 / ( GM) r3 , 3 ème loi de Kepler. T = 2 p (r3/(GM) )½. . . Disposition d’une série d'objets ponctuels sur une même orbite. Soit un ensemble d’objets, assimilables à des points matériels, mais de tailles et de masses différentes, satellisés autour de Saturne sur une même orbite circulaire de rayon r qu'ils parcourent tous dans le même sens. La figure 1 du tableau ci-dessous donne la configuration de ces objets à un instant de date donnée (les échelles de taille des objets, par rapport à Saturne, n’ont pas été respectées). On fait en outre l’hypothèse que les interactions gravitationnelles entre ces objets sont négligeables par rapport à celle exercée par Saturne sur chacun d’eux. 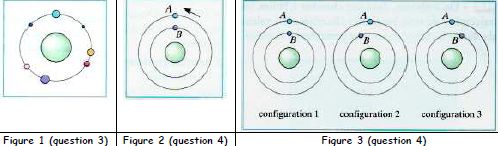Tous ces objets ont-ils la même vitesse sur l’orbite ? Justifier. La vitesse est indépendante de la masse des objets. Sur une même orbite circulaire, les objets ont la même vitesse. Comment évolue la structure de l’ensemble au cours du temps ? La structure de l'ensemble ne change pas au cours du temps. Disposition de deux objets ponctuels sur deux orbites de rayons différents. Soient deux objets A et B, assimilables a des points matériels, satellisés autour de Saturne sur deux orbites circulaires de rayon rA, et rB différents (rA > rB), mais de valeurs voisines. La figure 2 du tableau précédent donne la configuration de ces objets à un instant de date donnée : ils sont disposés de façon que la direction AB passe par S, le centre de Saturne ; la flèche indique le sens des mouvements (les échelles des rayons n'ont pas été respectées). Ici encore, on considère que l'interaction gravitationnelle entre ces deux objets est négligeable et que seule celle de Saturne intervient. À une date ultérieure, l’objet satellite A a effectué exactement une révolution autour de Saturne ; on souhaite savoir où se trouve l'objet B sur son orbite. Indiquer, en justifiant, laquelle des trois configurations proposées dans la figure 3 du même tableau est possible. D'après la 3è loi de Kepler, à la plus grande orbite correspond la plus grande période. TA > TB ( configuration 2 ). . Les anneaux de Saturne. Décrire le mouvement des particules constituant un <<anneau» de Saturne. Les différentes particules qui constituent un anneau sont sur des orbites de rayons pratiquement identiques ; elles ont donc toutes la même période. L'anneau, tout entier, tourne autour de Saturne avec une vitesse angulaire qui dépend de son rayon. Décrire sommairement le mouvement des anneaux les uns par rapport aux autres. Les différents anneaux tournent autour de Saturne avec des vitesses angulaires plus grandes pour les anneaux proches que pour les anneaux lointains ; ils "glissent" les uns par rapport aux autres. A l'aide de l'étude qui précède, en supposant valides les hypothèses faites au 3, montrer que si les anneaux de Saturne ont été a un moment donné d'un seul tenant (soudés les uns aux autres), il est peu probable qu'ils aient pu le rester. Si un anneau était très large, les différences de vitesse entre la périphérie de l'anneau et la partie intérieure provoqueraient des tensions et, à la longue, ces différentes parties finiraient par se disloquer. La sphère de Roche. Une autre raison explique en partie l’existence des anneaux de Saturne. Il existe une distance R0, appelée rayon de la sphère de Roche qui marque la limite entre une zone ou des satellites peuvent se former par assemblage de poussières, cailloux… qui s’étaient formés en même temps que l’astre et une zone où cet assemblage est rendu impossible par l’action de l’astre. Il s’agit dans la suite de déterminer les raisons de l’existence de cette limite.  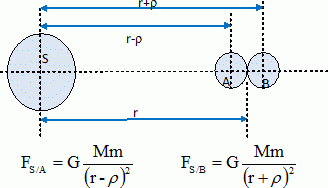On considère donc deux sphères homogènes identiques en contact de masse m et de rayon p telles que la distance de leurs centres A et B soit AB = 2p. Le centre de gravité P de l’ensemble des deux sphères tourne à une distance r du centre S de Saturne. Les points S, A, P et B sont alignés. 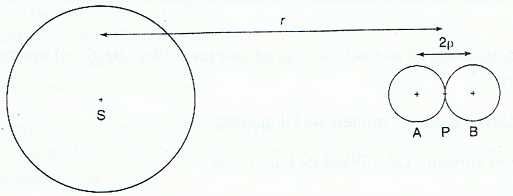Exprimer en fonction des paramètres utiles la valeur de la force d’attraction FAB qui s’exerce entre les sphères de centres A et B. 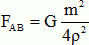Les deux sphères sont attirées par Saturne par deux forces de valeur FS/A et FS/B. Donner l’expression de FS/A , de FS/B puis de la différence FS/A-FS/B. Pourquoi les deux sphères ne sont-elles pas attirées de la même façon par Saturne ? Les centres des deux sphères ne se trouvent pas à la même distance du centre S de Saturne. Les forces de gravitation exercée par Saturne sur chaque sphère, sont différentes. La différence 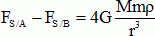  est encore appelée "force de marées". Cette différence d'attraction a tendance à séparer les deux sphères. R0, le rayon de la sphère de Roche, est tel que pour r = R0, on a : FAB = FS/A – FS/B. L’espace où les deux éléments A et B peuvent se regrouper pour donner naissance à un élément plus gros est-il défini par r < R0 ou par r > R0 ? Justifier la réponse. La différence 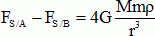  est encore appelée "force de marées". Ces forces sont proportionnelles à l'inverse du cube d'une distance. La force d'interaction attractive entre les deux sphères est : 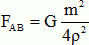. Cette force est proportionnelle à l'inverse du carré d'une distance. Si la distance diminue  ( r < R0 ),  les "forces de marées" l'emportent sur la force attractive FAB : les sphères se séparent. Si la distance augmente ( r >R0 ), la force attractive FAB l'emporte sur les "forces de marées" : les sphères ne se séparent pas. A votre avis , dans quelle zone se situent les anneaux de Saturne et où sont situés ses satellites ? Rayon intérieur du premier anneau : 74 milliers de kilomètres. Rayon extérieur du dernier anneau : 136 milliers de kilomètres. Rayon de l'orbite du satellite le plus proche de saturne, Janus : 159 milliers de kilomètres. .

menu