Lecture
des
informations sur un CD, effet Doppler, descente acrobatique. Concours
Audioprothèsiste Paris
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
Lecture des
informations stockées sur un CD.
On souhaite évaluer l’ordre de grandeur de la quantité d’informations
enregistrées sur un CD (compact disc) audio. L’encombrement spatial
d’un bit sur ce compact disc est de l’ordre de 2,0 µm2.
La
gravure du compact disc est faite du bord vers le centre, à partir d’un
rayon R= 5,80 cm jusqu’à un rayon r= 2,50 cm.
Quelle est la valeur de la surface que l’on peut utiliser pour
l’écriture des bits ?
p(R2-r2)=3,14(5,82-2,52)=86,05
~86 cm2.
Quelle est la quantité de bits ainsi stockés sur ce compact disc ?
86 108
/ 2,0 = 4,3 109 bits.
La vitesse linéaire de défilement du disque devant le faisceau laser
est constante v=1,22 m s -1 environ. Quelles
sont les
valeurs minimale et maximale de la vitesse angulaire de rotation du
disque lors de la lecture ?
w1
= v / R =1,22 / (5,80 10-2) =21,0
rad / s.
w2
= v / r =1,22 / (2,50 10-2) =48,8
rad / s.
L’ensemble
des pistes forme la spirale d’enregistrement : une piste ayant une
largeur constante e = 2,0 µm, évaluer la longueur de la spirale.
p(R2-r2) / e =86 / (2,0 10-4)
~ 4,3 103 m.
Combien
de bits sont lus par seconde ?
4,3 109
bits sont stockés sur une longueur de 4,3 103 m.
En une
seconde le
faisceau laser parcourt 1,22 m environ.
1,22*4,3 109
/ (4,3 103) =1,22 106 bits
lus par seconde.
Détermination
d'une vitesse par effet Doppler.
Les radars routiers utilisent l’effet Doppler pour mesurer la valeur de
la vitesse des véhicules.
Pour simplifier le problème, on considère un véhicule émettant un son
(E) s’approchant d’un observateur immobile (O) ; le véhicule et
l’observateur sont considérés comme ponctuels.
On travaille dans le référentiel terrestre et on suppose que la vitesse
du véhicule, constante, est très inférieure à la célérité de l’onde
sonore.
On notera - f la fréquence du signal produit par le véhicule émetteur ;
- fAPP la fréquence du signal reçu par
l’observateur fixe ;
- c la valeur de la célérité de l’onde sonore ;
- V la valeur de la vitesse de l’émetteur.
A la date t = 0, le véhicule E est à la distance D de l’observateur et
émet un bip sonore.
Donner l’expression littérale de la date t1 de
perception de ce premier
bip par l’observateur O.
t1 = D/ c.
Quelle est la distance d parcourue par le véhicule émetteur
pendant la période T du signal émis ?
d = VT.
A cette date T, quelle est alors la distance entre le véhicule E et
l’observateur O ?
D-d = D-VT.
A cette même date T, le véhicule émet un deuxième bip sonore.
A quelle date t2, l’observateur perçoit-il ce
second bip ?
t2 = T + (D-VT) / c.
3) Quelle est la durée qui sépare les deux bips consécutifs captés par
l’observateur ? Comment peut-on appeler cette durée ?
Période des bips reçus par
l'observateur : TAPP=t2 -t1 = T-VT / c = T(1-V/c).
Exprimer alors la relation
liant f, fAPP, V et c pour un tel
véhicule se rapprochant de l’observateur.
Le son perçu par l’observateur lui semble-t-il plus grave ou plus aigu
que le son émis ?
fAPP = 1/TAPP =f /(1-V/c).
fAPP > f, le son perçu est plus aigu.
|
| .
. |
|
|
Quelle est l’expression littérale de
la valeur de la vitesse V de
l’émetteur, en fonction de la célérité
du son c, de la fréquence f du signal produit, et de la fréquence fAPP
du signal perçu ?
1-V/c
= f / fAPP ; V = c(1-f / fAPP).
La loi établie par Christian Doppler
en 1842 trouva des applications
inattendues lorsqu’un physicien français, Hippolyte Fizeau (1819-1896)
décida de l’appliquer aux ondes
électromagnétiques et notamment à la lumière.
Comment est-il possible de déterminer si une galaxie s’approche ou
s’éloigne du système solaire ?
Si une
galaxie s'éloigne du système solaire, on observe un
décalage vers le rouge, appelé "redshift" , du spectre de la lumière
émise par l'étoile.
Quelle conception de l’origine de
l’Univers l’effet Doppler-Fizeau
permet-il de valider ?
Preuve
de l'expansion de l'univers.
|
.
|
|
Descente
acrobatique.
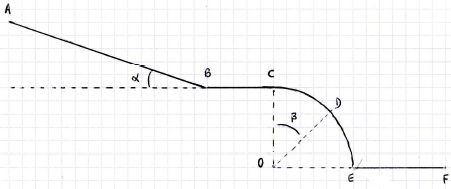
Un skieur descend une piste rectiligne AB, de longueur L1,
qui fait un angle a
avec l’horizontale. Toute la suite de son parcours se situera dans le
même plan vertical pris pour plan de figure. On assimile le skieur a un
point matériel M, de masse m, qui se déplace sur ABCDEF. On néglige la
résistance de l’air et on travaille dans le référentiel terrestre que
l’on suppose galiléen. Données : L1 = 200 m ; a =
20° ; r = 50 m ; m = 70 kg ; g = 10 m s-2.
Piste
enneigée AB :
Sur cette partie de la piste on considère que la force de frottement
est portée par la droite AB, opposée au sens du mouvement et a une
valeur constante f.
Le skieur part de A avec une vitesse nulle ; il arrive en B
avec la vitesse VB.
Etablir l’expression littérale de l’intensité f de la force de
frottement en fonction de m, g, L1 , a et VB.
Variation de
l'énergie cinétique du skieur : ½mv2B.
Le skieur
est soumis à
son poids, à la force de frottement et à l'action normale du plan.
Cette dernière étant perpendiculaire au plan, son travail est nul.
Travail moteur du poids en escente : mg L1 sin a.
Travail résistant des frottements : - f L1.
Théorème de l'énergie cinétique entre A et B : ½mv2B = mg L1 sin
a
-f L1.
f = mg sin a -½mv2B / L1.
Calculer cette intensité pour VB = 15 m s-1.
f = 70 (10 sin 20 -0,5*152 / 200)=200 ~2,0 102 N.
Piste verglacée BCDE
:
On néglige tous les effets dus aux changements brusques de pente en B,
C ou E. Sur cette partie de la piste on considère que la force de
frottement est nulle.
La partie BC de la piste est horizontale et de longueur L2
= 50 m.
Faire le bilan des forces sur cette portion de piste et montrer que la
vitesse en C est égale à la vitesse en B.
Le skieur
est soumis à
son poids et à l'action normale du plan. Ces deux forces étant
perpendiculaires à la vitesse, ne travaillent pas. L'énergie cinétique,
et en conséquence la vitesse du skieur, ne sont pas modifiées.
La partie CDE de la piste est un arc de cercle de rayon r = OC = OD =
OE (avec OC vertical et OEF horizontal). Sur cette partie CDE, on
repère le point D par l’angle ß que fait OD avec la verticale.
Trouver l’expression du carré de la vitesse de M en D, V2D , en fonction de VB
, r , g et cos ß.
Variation de l'énergie cinétique
du skieur : ½mv2D -½mv2B.
Travail moteur du poids : mgr(1-cos ß). L'action normale au plan ne
travaille pas.
Théorème de l'énergie cinétique
entre C et D : ½mv2D -½mv2B = mgr(1-cos ß). v2D =v2B +2gr(1-cos ß).
En
utilisant l’expression de la composante normale de l’accélération pour
un mouvement circulaire, établir l’expression de l’intensité R de la
réaction qu’exerce la piste sur le skieur au point D , en fonction de VD,
m , g, r et ß. En déduire finalement R en
fonction de VB , g , r et ß.
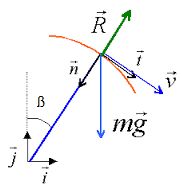
Suivant n : mg cos ß -R= mv2D / r ; R = m(g cos ß-v2D / r ). R = m( g(-2+3cos ß)-v2B / r).
Le
skieur commence à s’inquiéter sérieusement de ce qui va lui arriver en
E lorsqu’il se rend compte qu’il est en train de quitter le sol !
Calculer la valeur numérique ß0 de l’angle ß
pour lequel le point M quitte la piste CE.
R=0 dès que
le skieur quitte la piste. g(-2+3cos ß0)=v2B / r ; 3cos ß0=v2B / (gr) +2 ;
cos ß0=(v2B / (gr) +2) / 3 = (225 / 500 +2) / 3 =
0,817 ; ß0 = 35°.
|
|
|
Phase aérienne du
mouvement :
Le skieur ayant quitté la piste CE, il n’est plus soumis qu’à son poids.
Quel angle fait alors sa vitesse avec l’horizontale (lors de son
décollage) ? ß0 = 35°.
Quelle est la valeur de sa vitesse (lors de son décollage) ?
vD =(v2B +2gr(1-cos ß0)
)½= (225 +2*10*50(1-cos 35))½=20,2 ~20
m/s.
Quelles sont les coordonnées de D0,
point de décollage ? On prendra l’origine en O.
x0 = r sin ß0 = 50 sin 35,2 =28,8~29 m ; y0 = r cos ß0=40,85 ~41 m.
Quel est la nature de son mouvement ultérieur ? Chute libre.
Etablir l’équation de sa trajectoire.
On choisit
un axe vertical orienté vers le haut, origine en O et un axe horizontal
orienté vers la droite.
Accélération
: (0 ; -g) ;
vitesse initiale : ( 20,2 cos 35,2 ; -20,2 sin 35,2 ) soit ( 16,5 ; -
11,64) ; vitesse : (16,5 ; -gt-11,64 ) .
Position : x = 16,5 t +28,8 ; y = -½gt2 -11,64 t
+40,85 ; y = -5t2 -11,64
t +40,85.
t = (x-28,8) / 16,5; repport dans y : y = -5(x-28,8)2/
16,52-11,64 (x-28,8) / 16,5 +40,85.
y = -0,0184 x2 +0,352 x+ 45,93.
A quelle distance du point E touche-t-il le sol (sur la partie
horizontale EF) ?
y=0 au sol : résoudre -0,0184 x2
+0,352 x+ 45,93 = 0.
D = 0,3522+4*45,93*0,0184=3,50
; x = (-0,352 -1,87) / (-2*0,0184)=60,4
m.
|
|
|