QCM numérisation
d'un signal, équations horaires.
Concours audioprothèsiste Bordeaux 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
|
|
|
Une
seule réponse juste par question ; des points négatifs seront affectés
en cas de réponse fausse.
37. Si le chant d'un rossignol seul
est perçu avec un niveau d'intensité sonore de 52 dB, quel serait le
niveau sonore perçu dans le cas de 4 rossignols de même puissance
sonore ?
55 ; 58 ; 210 ; 61 ; 56,5.
l'intensité sonore quadruple et le niveau d'intensité sonore augmente
de 10 log 4 = 6 dB.
Réponse 52+6 = 58 dB.
38. Si 27 violons
jouant à la même puissance produisent un niveau sonore de 83 dB, quel
est le niveau sonore ( en dB) d'un seul violon ?
54,4 ; 56,0 ; 61,2 ; 68,7 ; 3,1.
Itotale = I0 108,3 = 10-12
*108,3 ~2,0 10-4 W m-2.
Intensité sonore d'un violon jouant seul : Itotale
/27 =7,4 10-6 W m-2.
Niveau sonore correspondant :
10 log(7,4
10-6 / 10-12)=68,7 dB.
39. Un mur de largeur a est éclairé par un
faisceau laser. Pour différentes largeurs de fente, on a mesuré la
demi-largeur angulaire q
de la tache centrale. Les résultats ermettent de construire le graphe
ci-dessous. En déduire la longueur d'onde du laser.
0,273 nm ; 1092 nm ; 0,546 µm ; 4,29 µm ; 54,6 µm.
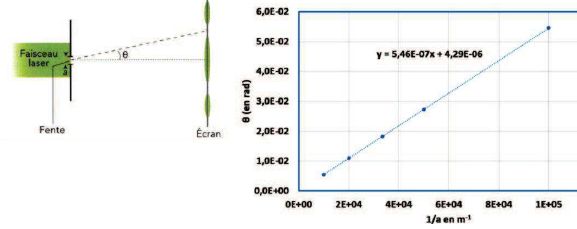
La pente de la droite donne la longueur d'onde en mètre, soit 5,46 10-7
m = 0,546 µm.
40.
Un mur de largeur a est éclairé par un
faisceau laser. Pour différentes largeurs de fente, on a mesuré la
demi-largeur angulaire q
de la tache centrale. Les résultats ermettent de construire le graphe
ci-dessous. En déduire la longueur d'onde du laser.
412 nm ; 236 nm ; 186 µm ; 576 nm ; 512 nm.
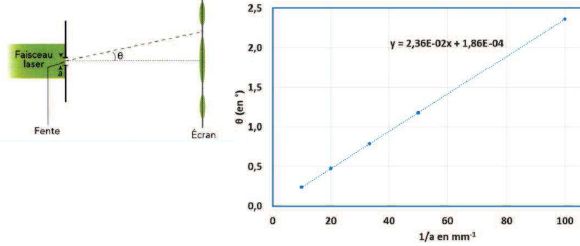
La pente de la
droite donne la longueur d'onde en millimètre, soit 2,36 10-2 degré mm.
2,36 10-2 *3,14 / 180
= 4,12 10-4 rad mm ou 4,12 10-7 rad m. l =412 nm.
41. Un
mur de largeur a est éclairé par un faisceau laser. Pour différentes
largeurs de fente, on a mesuré la demi-largeur angulaire q de la tache centrale. D =
70 cm. Quelle est la longueur d'onde du laser ?
702 nm ; 620 nm ; 434 nm ; 512 nm ; 408 nm.
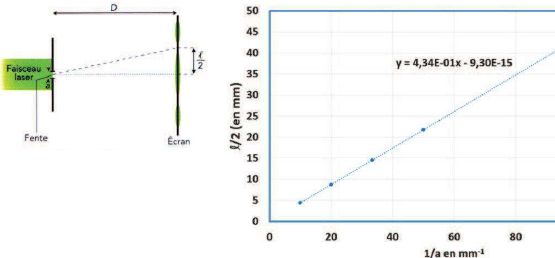 La pente de la droite vaut
l D = 0,434 en mm2. l =0,434 / 700 =6,2 10-4
mm =6,2 10-7 m = 620 nm.
La pente de la droite vaut
l D = 0,434 en mm2. l =0,434 / 700 =6,2 10-4
mm =6,2 10-7 m = 620 nm.
42. Déterminez la
fréquence d'échantillonnage du signal numérisé suivant :
400 Hz ; 5 kHz ; 10 kHz ; 5 MHz ; 4 kHz.
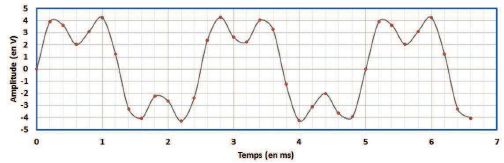
0,2 ms = 2 10-4 s entre deux mesures. Fréquence
d'échantillonnage f = 1/(2 10-4) =5000 Hz = 5 kHz.
43. Déterminer la
fréquence fondamentale du signal ci-dessus.
400 Hz ; 5 kHz ; 10 kHz ; 5 MHz ; 4 kHz.
Période T = 2,5 ms = 2,5 10-3 s ; f =1/(2,5 10-3)
= 400 Hz.
44. Une image numérique est généralement codée
en RVB 24 bits. Cela signifie que le nombre de couleurs possibles
s'élève à : 24 ; 576 ; 16 777 216 ; 16 752 364 ; 192.
256 *256*256 = 16 777 216.
45.
On reproduit le son d'une clarinette. La tension est ensuite numérisée
par un CAN 16 bits. La fréquence d'échantillonnage est réglée à 48 kHz.
Le débit binaire ( kbits /s) du flux audio est ( en kbps) : 262 ; 768 ;
12300 ; 49200 ; 48.
16 *48 = 768 kBps.
46.
Dans une piscine, un haut-parleur accroché à un mur émet dans l'air une
onde musicale de réquence f=338 Hz. La fréquence perçue dans l'eau par
un plongeur est :
276 Hz ; 338 hz ; 1491 Hz ; il ne peut pas entendre le son, qui n'a pas
été émis dans l'eau ( vrai) ; 77 Hz.
|
| .
. |
|
|
47.
Une onde lumineuse de longueur d'onde dans le vide 492 nm, se propage
dans l'eau. Sa longueur d'onde ( en nm) dans l'eau est : 492 ; 328 ;
654 ; 503 ; 370.
492 / neau = 492 / 1,33 ~370
nm.
48. Une onde lumineuse
de longueur d'onde dans le vide 492 nm, se propage dans l'eau. Cette lumière est
de couleur :
ultraviolette ; bleu clair( vrai) ; orange ; infrarouge ; magenta.
49. Par rapport au son, la lumière
se propage :
100 fois plus vite ; 10 000 fois plus vite ; 1 million de fois
plus vite ( vrai) ; 100 millions de fois plus vite ; 10 milliards de
fois plus vite.
50.
La force gravitationnelle exercée par la terre de mase M sur un corps
de masse m est donnée par :
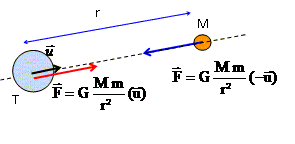 Réponse E. Réponse E.
51. On envoie un
fichier JPEG de 4 Mo par mail depuisun téléphone mobile au moyen d'une
connexion à un réseau hertzien dont le débit est d'environ 40 Mbps. La
durée du transfert des données ( hors durée d'accès au serveur ) est en
seconde :
0,1 ; 0,8 ; 5 ; 20 ; 1,25.
4,0 Mo ~ 4,0 106 octets ~ 8*4,0 106 bits ~3,2 107
bits.
3,2 107 / (40 106) =0,8 s.
52. Le sigfnal reçu
est la somme {signal à transmettre + bruit }. Pour pouvoir le décoder
correctement, il faut que le rapport en dB signal / bruit soit au
moins de 20 dB. Le rapport entre la puissance du signal reçu et la
puissance moyenne des parasites ( bruit) doit être au moins :
2 ; 10 ; 20 ; 100 ; 200.
10 log ( Psignal) / Pbruit) = 20 ; log ( Psignal) / Pbruit) = 2 ; Psignal / Pbruit = 100.
53. Le signal reçu est amplifié 10 fois. Le nouveau rapport en dB signal / bruit est de ( en dB) :10 ; 20 ; 23 ; 30 ; 200.
P signal amplifié= 10 (Psignal + Pbruit) ; on amplifie de la même manière le signal et le bruit, donc Psignal) / Pbruit) reste inchangé.
|
|
|
|
54
.
On donne le graphe d'une loi horaire décrivant l'accélération d'un
mobile au cours du temps. Le mobile ne peut se déplacer que suivant une
direction repérée par l'axe Ox, et, qu'à l'instant t=0, il possède une
vitesse de 36 km / h en x0 = 3 m.
Quelle affirmation coincïde avec la figure ?
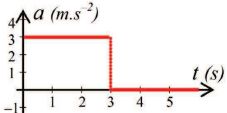
- La vitesse diminue linéairement à partir de t = 3 s.
- Le mobile a une vitesse constante à partir de t = 3 s. ( vrai). L'accélération devient nulle, le mouvement est uniforme.
- Le mobile ralentit à partir de t = 3 s et s'arrête.
- Le mobile ralentit à partir de t = 3 s et repart dans l'autre sens.
- Le mobile accélère jusqu'à t = 3 s puis se laisse mourir.
55. Durant les trois premières secondes du mouvement, la loi horaire de la vitesse est ( en unité SI) :
v(t) = 1,5 (t+3) ; v(t) = 3t+10 ; v(t) = 3t-12 ; v(t) = 3t +36 ; v(t)=0.
v(t) = at + v0 avec v0 = 36 /3,6 = 10 m /s et a = 3 m s-2. v(t) = 3 t+10.
56. Durant les trois premières secondes du mouvement, la loi horaire de la position est ( en unité SI) :
x(t) = 1,5 t2 +36 t ; x(t) = 3 t2 +10 t ; x(t) = 3t-12 ; x(t) = 1,5 t2 +36 t +3 ; x(t) = 1,5 t2 +10 t +3 ( vrai).
57. La vitesse atteinte à t = 3 s vaut :
47 km/h ; 167 km/h ; 38 m/s ; 51 m/s ; 63 m/s.
v(t=3) = 3*3+10 =19 m / s ou 19*3,6 ~68 km/h.
58. L'allure du graphe qui représente la loi horaire de la position x(t) au cours du temps est :
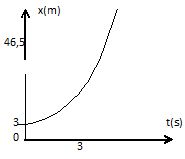 Réponse E. Réponse E.
|
59.
Afin de numériser un signal sonore, on utilise un microphone relié à
une carte d'acquisition de résolution 8 bits, utilisée sur le calibre
[-1 V ; +1 V ]. On enregistre pendant une durée de temps dt = 100 ms,
et de la manière la plus fidèle possible avec cette carte, un son de
fréquence 500 Hz. Le pas du convertisseur est ( en volt ) :
0,00078 ; 0,0078 ; 0,078 ; 0,78 ; 7,8.
Avec un CAN 8 bits, 256 valeurs sont possibles. La plage de valeurs est de 2 V= 2000 mV. Le pas du CAN est 2000 / 256 ~7,8 mV= 0,0078 V.
60. Un émetteur d'onde E se rapproche d'un récepteur fixe R. On note fE la fréquence de l'onde émise et fR la fréquence de l'onde reçue.
fR= fE ; fR< fE ; fR<= fE ; fR >= fE ; fR> fE (vrai).
|
|