Oscillateurs et mesure du temps. Concours kiné Assas 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . Jusqu'au milieu du XXème siècle seuls les systèmes oscillants permettaient de mesurer le temps. Le problème aborde quelques caractéristiques du pendule pesant en tant que système oscillant. Ce pendule est constitué d'un fil inextensible de longueur l, attaché en un point A fixe. Un solide de petite dimensions est fixé à l'extrémité du fil. La masse du fil est négligeable devant la masse m du solide. On écarte le pendule d'un angle q = 20° par rapport à sa position d'équilibre G0 et, à t=0, on le lâche sans vitesse initiale. Le pendule oscille librement. On néglige dans un premier temps les frottements. L'origine de l'énergie potentielle de pesanteur est prise en G0 d'altitude z=0. A chaque instant, la position du centre de gravité G du solide est repéré par l'angle q. m = 200 g ; l = 50 cm. Faire l'inventaire des forces appliquées au solide et les représenter. Le solide est soumis à son poids P et à la tension T du fil . 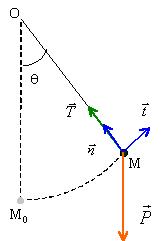Exprimer l'altitude z du solide en fonction de l et q. Sur le schéma q corespond à a et L à l. 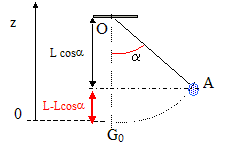z = l(1-cosq). En déduire que l'énergie potentielle de pesanteur peut s'exprimer par : Ep = mgl(1-cosq). Ep = mgz = mgl(1-cosq). Donner la valeur de la vitesse du solide au passage en G0. L'énergie mécanique se conserve : ½mv2 = mgl(1-cosq). v2 = 2gl(1-cosq) ; v = [2gl(1-cosq)]½. v = [2*9,81*0,50(1-cos20)]½=0,769 ~0,77 m/s. . . On donne l'évolution des formes d'énergie du système.   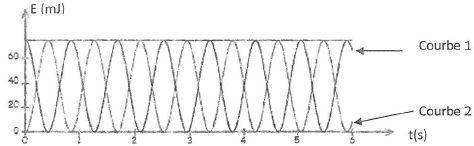Identifier les courbes représentant l'énergie cinétique et l'énergie potentielle. Courbe 1 : énergie potentielle ( sa valeur initiale n'est pas nulle ). Courbe 2 : énergie cinétique. Indiquer si le système étudié est soumis à des forces conservatives ou non conservative. Indiquer la valeur du travail de ces forces. ( sans aucun calcul). L'énergie mécanique étant constante, le système est soumis à des forces conservatives. Le travail de la tension est nul, cette force et à chaque instant perpendiculaire à la vitesse. Le travail du poids est égal à l'opposé de la variation de l'énergie potentielle soit ± 60 mJ. En montée de G0 à A le travail du poids ett résistant : -60 mJ. En descente de A à G0, le travail du poids est moteur : +60 mJ. . Identifier parmi les expressions suivante, l'expression correcte de la période propre du pendule. 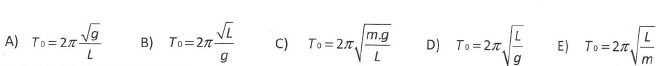[Longeur]½ = L½ ;  [g]½ = L½T-1 ; [longueur / g]½ = T ; 2 p est sans dimension. L'expression D est correcte. Quelle longueur doit-on donner au pendule si l'on souhaite qu'il batte la seconde ? T = 2 s ; L = T2g/(4p2) =4*9,81 /(4*3,142)=0,994~0,99 m. 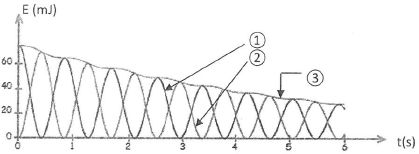L'étude énergétique d'un pendule simple dans une situation réelle donne les résultats suivants : Identifier chaque courbe. 1 : énergie potentielle ; 2 : énergie cinétique ; 3 : énergie mécanique. Quelle solution doit-on envisager pour que le pendule constitue une horloge fiable ? Il faut compenser régulièrement les pertes d'énergie mécanique. Le système est entretenu grâce à un système dit "échappement". .

menu