Dynamique
des fluides ; capteur de force.
Concours GEIPI 2015( Sti2d)
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Exercice
1.
Un
propriétaire décide d’équiper sa maison située à Nancy d'un système de
récupération des eaux de pluie. Sa toiture a une surface utile de 120
m². Les précipitations à Nancy sont données sur le graphique ci-dessous
en mm par mois.
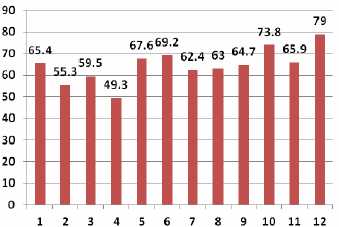
Calculer
le volume total de précipitation récupérable par an.
65,4 +55,3
+59,5 +49,3 +67,6 +69,2 +62,4 +3 +64,7 +73,8 +65,9 +79 =775,1 mm ;
1 mm
correspond à 1 L par m2 soit 0,7751 *120 ~ 93 m3.
On décide de retenir pour l'étude un volume récupéré annuel de 80 m3.
Calculer le rendement de récupération.
80 / 93
=0,86 ( 86 %).
La famille utilise 500 litres d’eau par jour. Calculer
l'autonomie en eau du ménage que vous exprimerez en jour.
80/0,500 = 160 jours.
Le complément d'eau sera prélevé du réseau de distribution d'eau
potable. En déduire la consommation quotidienne moyenne d'eau provenant
de ce réseau.
80 000 /365
=219 LJ-1 ; 500-219 =281 L J -1.
L'eau récupérée par les gouttières tombe dans une cuve située sous le
niveau du sol. L’eau est remontée grâce à une pompe immergée (en E),
vers un château d’eau. Celui-ci est toujours plein et sa surface située
à 9,5 m (en B) est en contact avec l'atmosphère. Le robinet C se situe
à 3,5 m de hauteur par rapport au sol.
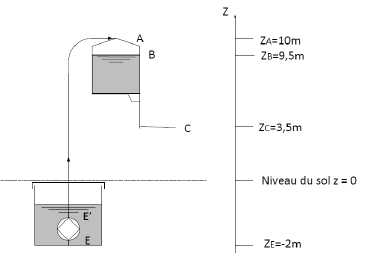 . .
Principe fondamental de l'hydrostatique appliqué entre M et N : PM
+ r.g.zM
= PN + rg.zN.
Préciser ce que signifie r et g
dans le principe fondamental de l'hydrostatique.
r : masse volumique du fluide en
kg m-3 ; g : intensité de la pesanteur
en m s-2.
Le fond de la cuve au point E est à 1,5 mètre sous la surface de l'eau
dans la cuve.
Calculer la pression PE en E.
PE = PB + rg(zB-zE) =1,0 105 +1000*10(9,5+2)=2,15 105 Pa ~2,1 105 Pa.
La pompe envoie l'eau jusqu'en A. La colonne d'eau E' A est estimée à
environ h = 10,5 m.
Calculer la pression nécessaire PE' à
la sortie de la pompe en E'.
PE' = PA + rg E'A=1,0 105 +1000*10*10,5=2,05 105 Pa.
En déduire la surpression minimale que doit assurer la pompe.
2,05 105-1,0 105 =1,05 105 Pa.
L'eau
tombe directement du château d'eau vers le robinet. Les tuyaux
d'alimentation du
robinet C ont un diamètre interne de D = 13 mm.
Equation de Bernoulli entre M et N : ½ r V²M
+ PM + r.g.zM
= ½ r
V²N + PN + r.g.zN
En appliquant l'équation de Bernoulli entre B et C et en négligeant la
vitesse d'écoulement en B, exprimer puis calculer la vitesse
d'écoulement en C.
½
r
V²B + PB + r.g.zB
= ½ r
V²C + PC + r.g.zC.
½ r
V²C =(
PB -
PC)+
r.g.(zB
-zC)
;
V²C
=2(
PB -
PC)/
r.+2g.(zB
-zC)
;
VC
=[2(
PB -
PC)/
r.+2g.(zB
-zC)]½
;
VC
=[0.+2g.(zB
-zC)]½
= (2gBC)½.
VC
=(2*10*6)½ = 10,95 ~11 m s-1.
Cette
vitesse en C étant trop importante, on décide
de la limiter à V = 7,10 m.s-1.
Donner l'expression du débit volumique maximal Qv
du robinet C. Calculer Qv en litres par minute.
Qv = pD2/4 vc =3,14 *0,0132 / 4 *7,1 =9,4 10-4 m3 s-1 ;
0,94 L s-1 ou 0,94*60 =57 L min-1.
|
| .
. |
|
|
Exercice
2.
Un capteur de force est constitué de 4 jauges de contrainte collées sur
une pièce métallique appelée corps d'épreuve. On souhaite que son domaine de déformation
soit linéaire.
Indiquer dans le document réponse le ou les qualificatifs
correspondant au domaine de déformation linéaire.
Le domaine est élastique et réversible.
Les jauges de contrainte sont des conducteurs ohmiques dont la
résistance varie avec la déformation sous l'effet d’une force F que l'on désire mesurer .
La résistance des conducteurs R s'écrit R = rL/S.
r : résistivité du matériaux du conducteur ; L : longueur du conducteur ; S : section du conducteur
On admet constant le volume du conducteur lors de sa déformation.
Indiquer
les signes des variations de longueur, de section et de résistance
subies par la jauge lors d'une extension, puis d'une compression.
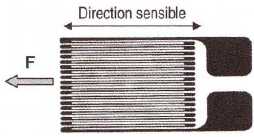
Extension : la longueur augmente, la section diminue, la résistance augmente.
Compression : la longueur diminue, la section augmente, la résistance diminue.
|
.
|
|
Pour
augmenter la sensibilité du dispositif, les jauges sont montées en pont
de Wheatstone (montage ci-dessous). En l'absence de force F, les 4
résistances sont identiques, de valeur
nominale R0. En présence de forces, 2 jauges voient leur résistance augmenter: r1 = r4 = R0 + DR. Les deux autres voient leur résistance diminuer : r2 = r3 = R0 - DR.
La variation DR vérifie la relation DR /R =k F.
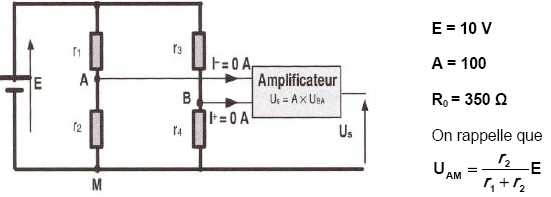
Exprimer UAM en fonction de E, R0 et DR.
UAM = r2 /(r1+r2) E =(R0 - DR) E / (2R0).
Exprimer UBM en fonction de E, r3 et r4, puis en fonction de E, R0 et DR.
UBM = r4 /(r3+r4) E =(R0 + DR) E / (2R0).
Démonter que UBA = DR E / R0.
UBA =UBM +UMA =UBM -UAM =(R0 + DR) E / (2R0) - (R0 - DR) E / (2R0) =DR E / R0.
L’amplificateur permet d'adapter la tension Us = A . UBA. On obtient un appareil de mesurage dont la fonction est de lier la tension de sortie Us à la force F.
Exprimer Us en fonction de E, R0, DR et A.
Us = A . UBA = A DR E / R0.
Montrer que la tension Us est proportionnelle à la force F.
DR / R0 = k F ; Us = A k E F.
Lorsque l'on soumet le corps d'épreuve à une force F0 = 1000 N, on mesure Us0 = 440 mV.
Exprimer k puis calculer sa valeur numérique en n’oubliant pas son unité.
k = Us0 /(AEF) =0,440 /(100*10*1000)=4,4 10-7 N-1.
Exprimer DR en fonction de E, A et R0 puis calculer DR.
Us0 = A DR E / R0 ; DR =Us0 R0 /(AE)=0,440* 350 /(100*10)=0,154 ~0,15 ohm.
|
|
|