Filtre électronique. Concours ITPE 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . On établit à l'entrée du filtre suivant une tension sinusoïdale u1(t) de pulsation w.On adopte la notation complexe et on note w02 =1/(LC) et Q20=Lw0/R. Etude qualitative. Rappeler en quoi est équivalent en basse et en haute fréquence, un condensateur. Même question pour une bobine. En basse fréquence, un condensateur se comporte comme un interrupteur ouvert.  A haute fréquence, il se comporte comme un interrupteur fermé. En basse fréquence, une bobine se comporte comme un interrupteur fermé.  A haute fréquence, elle se comporte comme un interrupteur ouvert. En raisonnant à l'aide de schémas équivalents et sans calculs, préciser le comportement de ce circuit à basse et à haute fréquence. En basse fréquence, il s'agit d'un dipole résistif ; en haute fréquence le circuit est ouvert. Etude en échelle linéaire. Déterminer l'expression de la fonction de transfert du montage H = U2/U1.  Condensateur et résistor sont en dérivation ; impédance complexe de l'ensemble : Impédance totale du circuit : Fonction de transfert : on pose x = w / w0. Quelle inégalité doit vérifier Q0 pour que la courbe représentative de |H| en fonction de w présente un maximum ? Quand x tend vers 0, |H| tend vers 1 et quand x tend vers l'infini |H|tend vers zéro. Dérivons |H| par rapport à x et annulons cette dérivée. . . Quelle est alors en fonction de w0 et Q0 la pulsation w1 de l'extrémum Hmax et la valeur de Hmax ? 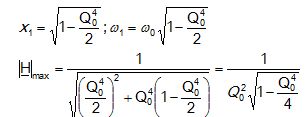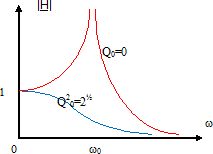Représenter les deux allures possibles ( selon la valeur de Q0) de la courbe représentative de |H| en fonction de w en faisant apparaître les points de pusation w=0 et w = w0.  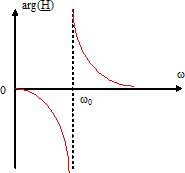Tracer l'allure de arg(H) en fonction de w. arg(H) =-Q20x / (1-x2). . Etude en échelle semi-logarithmique. Rechercher les équations des diretions asymptotiques de la courbe 20 log(|H|) = f(log w). 20 log(|H|) = -10 log[(1-x2)2+(Q20x)2] Lorque x tend vers zéro, 20 log(|H|) est équivalent à -10 log 1 = 0. L'asymptote est une droite horizontale. Losque x devient grand, 20 log(|H|) est équivalent à -10 log x4 =-40 log x. Lorsque x = 1, 20 log(|H|) est égal à -10 logQ40. 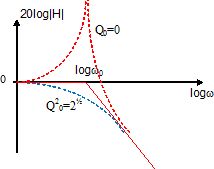Tracer les deux directions asymptotiques et représenter les deux allures possibles des courbes. .

menu