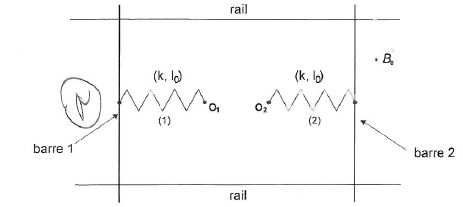
Couplage électromécanique. Concours ITPE 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Deux barres métalliques peuvent glisser sans frottement sur deux rails parallèles et distants de "a". Chaque barre possède une masse m, une résistance ½R et reste perpendiculaire aux rails. Les deux ressorts sont identiques ( constante de raideur k, longueur à vide l0). Le système est placé dans un champ magnétique B0 perpendiculaire au plan des rails. A l'instant initial le ressort 1 est comprimé ( sa longueur vaut l1(t=0) =l0-a' et le ressort 2 n'est ni détendu ni comprimé. Les vitesses initiales sont nulles. Etude mécanique. On pose w02 =k/m et l = B02 a2 / (mRw0). Les phénomènes d'autoinduction sont négligés. 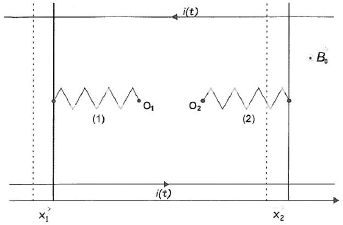On note x1(t) et x2(t) les déplacements des deux barres par rapport à leurs positions d'équilibre. Elles sont soumises aux forces exercées par les ressorts et aux forces de Laplace. On notera i le courant engendré par le mouvement des barres dans le champ magnétique B0. Dispositif hors équilibre. On s'intéresse à la barre 1. Exprimer en fonction de k et x1 la force exercée par le ressort 1. T1 = k x1. ( suivant le sens contraire de l'axe si x1 positif ). Exprimer la résultante des forces de Laplace exercées sur la première barre. F1 = B0 i a. ( suivant le sens contraire de l'axe). En déduire l'équation du mouvement de la première barre. m x"1 = -kx1 -B0i a. x"1 +k/m x1 =-B0i a / m. x"1 +w02 x1 =-B0i a / m.(1) Exprimer l'équation du mouvement de la seconde barre. T2 = k x2. ( suivant le sens contraire de l'axe si x2 positif ). F2 = B0 i a. ( suivant le sens de l'axe). m x"2 = -kx2 +B0i a. x"2 +k/m x2 =+B0i a / m. x"2 +w02 x2 =+B0i a / m.(2) . . Etude électrique. On note F le flux du champ magnétique B0 à travers le cadre de surface S constitué par l'ensemble ( rails + barres). Exprimer ce flux en fonction de B0 et S. Les vecteurs champ magnétique et surface sont colinéaires et de même sens. F = B0S. Exprimer S en fonction de a, x1 et x2. S = a ( O1O2 + l0-x1 +l0+x2). A l'aide de la loi de Faraday en déduire l'expression de e, force électromotrice induite dans le circuit. e = -dF/dt =-B0a(-x1'+x2'). Donner l'expression de i en fonction de B0, a, x1' et x2'. La résistance des rails étant négligée, i= e / R =B0a(x1'-x2')/ R. Par suite :x"1 +w02 x1 = B20 a2 / (Rm)(x2'-x1') = -l w0( x'1-x'2) x"2 +w02 x2 = B20 a2 / (Rm)(x1'-x2')= l w0( x'1-x'2) Ces deux résultats sont donnés dans le texte. . Réécrire le système précédent en effectuant le changement de variable S =x1+x2 et D = x1-x2. S' =x'1+x'2 et D' = x'1-x'2. S" =x"1+x"2 et D" = x"1-x"2. Addition des deux équations : S" +w02 S =0. Soustraction des deux équations : D" +w02 D =-2lw0D'. Décrire ( sans calculs) le mouvement des deux barres dans le cas où D=0. On retrouve le cas d'un oscillateur harmonique. Exprimer S(t) et D(t). On suppose que l est compris entre 0 et 1. S(t) =  A cos(w0t + B). A et B sont des constantes. S(t=0) = A cos B =l0-l1. S' (t=0)=0 = -Aw0 sin( B)d'où B =0.  S(t) =  (l0-l1) cos(w0t). D" +2lw0D'+w02 D =0. Equation caractéristique : r2 +2lw0 r +w02 =0. Discriminant D =4w02(l2-1). On pose  : w = w0(1-l2)½. Solutions : r1 =w0 (-l +j(1-l2)½) =-lw0 +jw et r2 =w0 (-l -j(1-l2)½) =-lw0 -jw . Par suite : D = C exp(-lw0t)cos (wt+E) avec C et E des constantes. D(t=0) =C cos E =l0-l1. D' (t=0)=0 = -C(lw0 cos E +wsin E )=0 soit tan E =- lw0 /w .   Bilan énergétique. En multipliant les équations (1) et (2) par respectivement x'1 et x'2, effectuer un bilan énergétique. On pourra faire apparaître la puissance électrique ei et les puissances des efforts de Laplace PL1 = -B0i a x'1 et PL2 =B0i a x'2 s'exerçant sur les barres.   x"1x'1 +w02 x1x'1 = -B0i a x'1 / m et x"2x'2 +w02 x2 x'2=+B0i a x'2/ m. x"1x'1 - x"2x'2 + w02 ( x1x'1-x2 x'2) =-B0i a (x1'-x2')/ m avec e=B0a(x1'-x2'). m (x"1x'1 - x"2x'2) +mw02 ( x1x'1-x2 x'2)=-ei. m (x"1x'1 - x"2x'2) +k (x1x'1-x2 x'2)= -ei. ½m (dx' 21/dt- dx' 22/dt) +½k (dx21/dt-dx22/dt)= -ei. ½m (d(x' 21-x' 22)/dt) +½k (d(x21-x22)/dt)= -ei. On pose Ec =½m(x' 21- x' 22 ), énergie cinétique et Ec =½k(x' 21+ x' 22 ), énergie potentielle. dEc/dt + dEp/dt =-ei = -Ri2. .

menu