Automobile :
consommation, freinage, énergie cinétique, choc frontal.
Concours général Stl 2012
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Consommation
d'un véhicule.
On considère un véhicule de masse totale M = 1300 kg ayant un
mouvement rectiligne uniforme à la vitesse v0
= 90 km/h. On suppose que l'ensemble des frottements aérodynamiques et
la résistance au roulement sont modèlisables par une force FR
de sens opposé au déplacement, d'intensité constante 900 N. Le moteur
exerce une force motrice FM que l'on supposera d'intensité
constante.
Dresser
l'inventaire des forces extérieures exercées sur le véhicule et les
représenter sans souçi d'échelle.
Poids ( verticale vers le bas, valeur Mg) ; action normale au plan ;
force de frottement FR et force motrice FM.
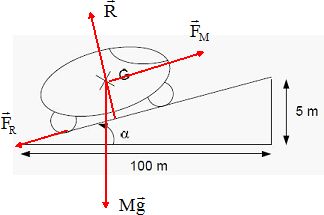
Déterminer
a.
tan a = 5 / 100 = 0,05 ; a =2,86 ~2,9 °.
Calculer
la valeur de FM.
La somme vectorielle des forces appliquées à la voiture est nulle. Sur
un axe parallèle au plan orienté vers le haut :
-Mg sin a -FR +FM
=0 ; FM
=Mg
sin a +FR +
1300*9,81 sin 2,86 +900 =1,537 103 ~1,54 103 N.
Calculer le travail WM
de cette force pour un trajet durant 1 h.
Distance
parcourue en 1 h : d=90 km =9,0 104 m. WM = FM
d = 1,537
103 *9,0
104 =1,38 108 ~1,4 108 J.
Calculer l'énergie
thermique Q nécessaire. Le
rendement du moteur thermique est de 30 %.
Q = WM
/ 0,30 = 1,38
108 /0,30 =4,6 108 J = 460 MJ.
Calculer la
consommation en L h-1 du véhicule sur route pentue.
Pouvoir calorifique du gazol : 35 MJ L-1.
460/35 ~13 L h-1.
Même
question sur route horizontale. Le travail du poids est nul et FM
= FR = 900 N.
W'M = 900*9 104 = 8,1 107 J = 81 MJ. Q
= 81/0,3 ~270 MJ ; 270/35 =7,7 L h-1.
|
| ...
.. |
|
|
Freinage du
véhicule.
La
distance d'arrêt est la distance totale parcourue pendant le temps de
réaction du conducteur et le freinage du véhicule jusqu'à l'arrêt
complet. Le temps de réaction du conducteur est tR ~ 1 s.
Pendant ce temps le véhicule parcourt la distance dR. Le
temps de freinage est noté tF ; la distance parcourue
pendant ce temps est notée dF.
La distance d'arrêt est dA = dF + dR.
On considère un véhicule de masse M = 1300 kg se déplaçant sur route
horizontale à la vitesse initiale v0=90 km/h.
Exprimer
et calculer dR.
Pendant le temps de réaction le mouvement est uniforme à la vitesse v =
90 / 3,6 =25 m/s.
dR = v0 tR = 25*1 = 25 m.
Durant
le freinage le mouvement du véhicule est rectiligne uniformément varié.
On désigne par a la valeur absolue de l'accélération.
Donner l'expression
de la vitesse v du véhicule durant la phase de freinage.
La vitesse est une primitive de l'accélération et la vitesse initiale
est v0 : v = at+v0.
Donner l'expression
de dF.
La distance est une primitive de la vitesse. dF = ½at2
+ v0t + constante.
La constante est déterminer par la position à la date t=0. Cette
constante est choisie égale à zéro.
Montrer que dF
= v02/(2a).
v = 0 = atR +v0 ; tR = -v0/a
; dF = ½a(-v0/a)2 + v0(-v0/a) = -½v02/a. ( a
est négatif, la vitesse diminue )
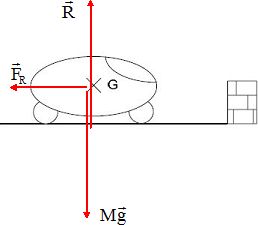
Dresser l'inventaire
des forces exercées sur la voiture pendant le freinage et les
représenter.
Le poids ( verticale, vers le bas, valeur Mg), l'action normale du
support et la froce de freinage FR. La force motrice est
nulle, le conducteur cesse d'accélérer.
Donner l'expression
de FR pendant le freinage.
La seconde loi de Newton conduit à FR = M|a|.
Le coefficient d'adhérence f des pneus sur la route est donné par : f =
FR/P.
Exprimer
f en fonction de a et g. f = M|a| / (Mg) = |a|/g.
Montrer
que dF = v02/(2fg).
dF = ½ v02/|a| =½v02/(gf).
Donner
l'expression de dA et compléter le
tableau.
dA = dR +dF = v0+½v02/(gf).
vitesse
( km/h)
|
vitesse
(m/s)
|
dR
sur sol sec (f = 0,8)
|
dR
sur sol humide (f = 0,4) |
50
|
50/3,6
~14
|
~27
|
39
|
90
|
25
|
64,8
|
104,6
|
130
|
~36
|
119
|
201
|
.
|
.
|
|
On peut montrer que la distance
de freinage dans le cas d'une route pentue est : dF=v02
/(2g(f+p) où p est la déclivitée de la pente ( valeur algébrique).
Par analyse
dimensionnelle, déterminer l'unité de p.
"p" étant ajouté à "f", "p" a la même dimension que
"f".
Or "f" est le rapport de deux forces ; "f" est sans dimension. Par
suite "p" est sans dimension.
Dans
le cas d'un véhicule descendant une pente, quel est le signe de la valeur
algébrique de la déclivité p ?
La vitesse croît en descente ;
la distance d'arrêt va augmenter
"p" figure au dénominateur ; ce dernier doit diminuer ; "p" sera
négatif.
Influence
de la valeur de l'énergie cinétique sur le freinage.
On considèrera le cas d’un véhicule de masse totale M = 1 300 kg se
déplaçant sur route horizontale. Voyant un obstacle, le conducteur
freine et la vitesse du véhicule passe de v0 au point O à la
valeur
vA= 0 km/h au point A ( situé avant l'obstacle).
Rappeler
l’expression de l’énergie cinétique E du véhicule en fonction de sa
vitesse v et de sa masse totale M.
Ec = ½Mv2 dans le cas de la translation.
Calculer
la variation DEc d’énergie cinétique
entre les points O et A dans deux cas :
v01 = 150 km/h = 150/3,6 m/s = 41,67 m/s ; DEc =0-0,5 *1300 *41,672
= -1,13 106 J = -1,13 MJ.
v02
= 130 km/h = 130/3,6 m/s = 36,11 m/s ; DEc =0-0,5 *1300 *36,112
= -8,48 105 J = -0,848 MJ.
Sous
quelle forme d’énergie est transformée l’énergie cinétique lors de la
phase de freinage ?
L'énergie cinétique est convertie en énergie thermique.
On suppose que 70 % de cette variation d’énergie cinétique
contribue à l’élévation de la température des freins.
Calculer
l’énergie échangée sous forme thermique Q dans les deux cas précédents.
Energie reçue par les freins : Q1 = 0,70 *1,13 =0,79 MJ ; Q2
= 0,7 *0,848 =0,59 MJ.
La masse totale des disques de frein est mD = 9 kg, la
capacité thermique du matériau constituant les disques vaut cD
= 460 J.kg–1.K–1 et la température des disques
avant freinage est T0 = 35 °C.
Calculer
la température TD des disques à la
fin de la phase de freinage dans les deux cas précédents.
Q = mD cD(TD-T0) ; TD = T0 +Q /( mD cD)
; TD 1=35 +7,9 105
/(9*460)=226 °C ; TD 2=35 +5,9 105
/(9*460)=178 °C.
On suppose
que, les pneus, proches des disques de frein, acquièrent une
température proche de TD peu de temps après la fin de la
phase de freinage.
Illustration du
phénomène d’éclatement ou d’explosion d’un pneu en 4 étapes :
- Échauffement de l'air dans le pneu qui se dilate et provoque une
augmentation de la pression.
- Lorsqu’il est chauffé autour de 185 °C le caoutchouc commence à se
dégrader, produisant des gaz et des matières inflammables, ce qui
augmente encore la pression dans le pneu.
- Si l’apport de chaleur continue, l'accumulation de gaz et de matières
inflammables due à la dégradation du caoutchouc continue.
- Lorsque la concentration critique des gaz et des matières
inflammables est atteinte en présence d'oxygène à la température et
pression d'auto allumage, il y a explosion.
Conclure
sur les différences de risques encourus lors d’un freinage d’urgence à
150 km/h et à 130 km/h.
Lors d'un freinage d'urgence à 150 km/h, les pneus risquent d'éclater.
|
|
|
Étude d’un choc
frontal :
On considèrera le cas d’un véhicule de masse totale M = 1 300 kg se
déplaçant sur route horizontale. Voyant un obstacle, le conducteur
freine mais n’arrive pas à éviter le choc. Lorsqu’il percute
l’obstacle, la
vitesse du véhicule au point B vaut vB = 50 km/h.
La diminution de longueur de l’avant du véhicule par déformation des
éléments mécaniques est de 0,60 m (à l’arrêt total).
On suppose que la force de déformation Fd exercée par
l’obstacle est constante. On considérera que cette force sera la seule
à prendre en compte durant le choc.
On désigne par aC la valeur absolue de la décélération
supposée constante pendant le choc.
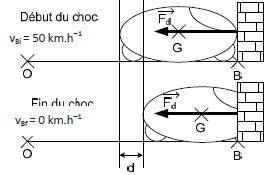
En cas de choc frontal,
l’énergie cinétique d’un véhicule est dissipée par le travail de
déformation de sa partie avant.
Exprimer
et calculer l’intensité Fd de la force de
déformation.
Variation d'énergie cinétique : 50 km/h = 50 /3,6 = 13,89 m/s. DEc =0-½MvB2
= 0,5*1300*13,892 = -1,25 105 J.
Travail de la force FD : W = -FD d ; théorème de
l'énergie cinétique : DEc
= -FD d ; FD = 1,25 105 /0,60 =2,09 105 ~2,1 105 N.
En utilisant la
relation fondamentale de la dynamique, en déduire la valeur de la
décélération aC.
aC =-FD/M =-2,09 105 /1300 =-1,61 102
m s-2.
Le prétensionneur de ceintures de sécurité est un dispositif de
sécurité qui s’active en cas de choc pour réduire le jeu entre la
ceinture et coupler le conducteur au véhicule. Il se déclenche si la
vitesse du véhicule
est supérieure à 24 km/h lors d’un choc frontal et si la
décélération est supérieure à 2,5 g.
En prenant pour l’accélération de la pesanteur g, la valeur g = 9,81 m.s-2,
déterminer
si le prétensionneur se déclenche lors du choc.
|aC|/g =1,61 102 /9,81 ~16,4. Le prétentionneur
se déclenche.
Existe-t-il
d’autres dispositifs de sécurité passive permettant d’éviter au
conducteur des lésions trop graves ? Préciser pour chacun de ces
dispositifs leur intérêt.
Les airbags diminuent les dommages dus aux chocs entre les passagers.
Le pare-brise et les vitres évitent les projections à l'intérieur du
véhicule.
L'appuie-tête évite le "coup de lapin".
Les barres de protection latérales dans les portières évitent trop de
déformation au véhicule.
|
|
|