Mesure de masse
extrèmement faible.
Concours général 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Les
vecteurs sont
écrits en gras et en bleu.
Pour
une mesurer une masse, il n’est pas nécessaire de faire référence à un
contre-poids. Il est possible d’utiliser une autre force, comme par
exemple la force de rappel élastique d’un ressort de raideur k, de
longueur instantanée l
et de longueur à vide l0
:
F
= - k(l-l0) ux.
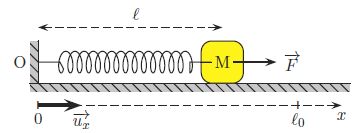 On
dispose d’un ressort de masse négligeable muni d’un crochet de
suspension, d’une règle graduée, d’un jeu de masses marquées et d’un
objet de masse inconnue.
On
dispose d’un ressort de masse négligeable muni d’un crochet de
suspension, d’une règle graduée, d’un jeu de masses marquées et d’un
objet de masse inconnue.
Proposer un protocole expérimental permettant d’avoir accès à la masse
inconnue par application
de la seconde loi de Newton à l’équilibre. On établira l’expression de
cette masse en fonction des
paramètres du problème et on discutera les différents types de mesurage
à effectuer pour obtenir le résultat.
Le solide suspendu au
ressort est soumis à la tension du ressort et à son poids. A la
position d'équilibre poids et tension sont opposées. k(L-L0) = mg.
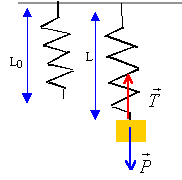
Accrocher des masses
marquées connues m ( 50 g , 100 g , 150 g, 200 g ....) au ressort
et noter à chaque fois l'allongement x de ce dernier. Tracer la courbe
x = f(m).
Suspendre le solide de
masse inconnue au ressort, noté son allongement et utiliser le graphe
pour déterminer sa masse.
Cette
méthode est très efficace pour des masses courantes mais elle devient
impossible à mettre en oeuvre lorsque la masse à mesurer est
extrêmement faible. La sensibilité du dispositif ne permet pas le
recours à une mesure statique basée sur la détermination d’une position
d’équilibre.
On fait alors souvent appel à un phénomène périodique pour en déduire
la valeur de la masse inconnue.
On s’intéresse à nouveau au ressort précédent. L’une de ses extrémités
est fixe dans le repère d’étude et le ressort peut s’étirer ou se
comprimer verticalement le long de l’axe dirigé par la pesanteur noté
(Oz).
On fixe à son autre extrémité un objet de masse m et de centre de masse
G. On choisit comme origine le point O correspondant à la position de G
au repos et on repère à tout instant la position de l’objet par sa
coordonnée z(t) le long de (Oz). On écarte l’objet de sa position
d’équilibre d’une distance z0 vers le bas puis on le lâche
sans vitesse initiale à t = 0 s.
Déterminer l’équation différentielle vérifiée par le centre de masse G
au cours du temps, lorsque
l’objet n’est soumis qu’à son poids et à la force de rappel élastique T.
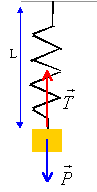 |
Ecarté de sa position d'équilibre le ressort
oscille : L= Léq +z
mg-k(L-l0)= m d²z/dt²
mg-k( Léq +z-l0)=
m d²z/dt²
mg-k( Léq -l0)
- kz =m d²z/dt² ; or mg = k(Léq-L0)
m
d²z/dt² + k z=0 (1)
On pose w02
= k/m
On retrouve
l'équation différentielle d'un oscillateur harmonique.
|
.
|
| ..
.. |
|
|
Une solution de l’équation différentielle peut
se mettre sous la forme : z(t)=A cos(2pt/T0 +F) ou A et F sont des
constantes positives non nulles.
Déterminer l’expression de T0 en fonction de k et de m, puis
calculer les valeurs de Zm et de F.
w0 =2p/T0 =( k/m)½. T0 =2p( m / k)½.
z(t=0)
=z0 = cos(F); z0 étant
positif, F est nul
z'(t)= -A2p/T0 sin(2pt/T0 +F) ; z'(t=0)=0 = -A2p/T0 sin(F) .
|
|
|
.
|
|
On
modifie légèrement la masse de l’objet que l’on note à présent m′ = m +
dm de
sorte que dm est
négligeable devant m.
Déterminer la nouvelle expression de T0, notée T′0,
en fonction de T0, m et dm. On
pourra utiliser
l’approximation (1 + x)�a
≃ 1 + ax lorsque
x → 0.
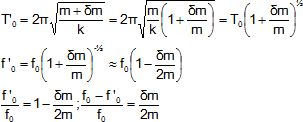
Sachant qu’il est possible de mesurer facilement des fréquences à 1 Hz
près, calculer la fréquence f0 associée à T0
permettant de mesurer une variation de masse de 1 μg pour une masse de
l’objet initial m = 1 g.
f0
= 2(f0-f '0)m / dm = 2*10-3
/10-6=2 kHz.
|
|
|