Etude d'une balance romaine. Concours général 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Les vecteurs sont écrits en gras et en bleu. Le principe d'une balance est d'établir un équilibre autour d'un axe de rotation fixe par compensation des efforts de deux masses sur la balance. On dispose d'une barre filiforme homogène, parfaitement symétrique, de longueur 2l et pouvant tourner autour d'un axe fixe D, perpendiculaire à la barre et passant par son centre O. De part et d'autre de O, chaque bras de la balance dispose d'un crochet de pesée dont le point d'attache peut être ajusté tout le long du bras. On s'intéresse aux trois situations expérimentales ci-dessus. Cas 1 : on attache une masse M à l'extrémité gauche de la barre maintenue horizontale, puis on laisse cette dernière évoluer librement en la libérant sans vitesse initiale. Cas 2 : on attache une masse M à chaque extrémité de la barre, puis on laisse cette dernière évoluer en la libérant librement à partir d'une situation non horizontale en la libérant sans vitesse initiale. Cas 3 : on attache une masse M à l'extrémité gauche de la barre maintenue horizontale ainsi qu'une seconde masse M en un point situé avant l'extrémité droite de la balance, puis on laisse cette dernière évoluer librement en la libérant sans vitesse initiale. On se focalise uniquement pour commencer sur l'étude du cas 1. Décrire l'état final de la balance après une évolution libre. Quel type de mouvement a entraîné la présence de la masse sur le crochet ? La tige tourne pratiquement d'un quart de tour dans le sens contraire des aiguilles d'une montre puis s'immobilise contre le bâti.. Faire l'inventaire des forces extérieures qui s'exercent sur la barre mobile dans le cas 1. Poids de la masse M, verticale vers le bas, valeur Mg, appliquée sur le crochet. Poids de la tige, verticale vers le bas, appliqué en O. Réaction de l'axe en O. Peut-on déterminer la position finale adoptée par la barre à partir de la seule utilisation de la seconde loi de Newton appliquée à la barre ? Non, l'effet d'une force dans le cas de la rotation, dépend de la valeur de la force et de sa position par rapport à l'axe de rotation. Ainsi, l'effet d'un couple de forces est la rotation, bien que les deux forces constituant ce couple soient opposées.   On dispose en mécanique, en plus de la seconde loi de Newton,d'une loi appelée " loi du moment cinétique" qui permet de rendre compte des observations effectuées dans les situations analogues à celle du cas 1. On définit, par rapport à un point A, le moment d'une force s'appliquant en un point M. Exprimer le moment en O de chacune des forces extérieures qui s'appliquent à la barre dans le cas 1 à l'état initial. Le poids de la tige et l'action de l'axe sur la barre passent par O : ces forces ont un moment nul par rapport à O. Moment du poids de la masse M : La somme vectorielle de ces moments n'est pas nulle. Par contre dans l'état final, le point M est pratiquement sur la verticale passant par O : dans ces conditions le bras de levier est nul et la somme vectorielle des moments est nulle. .. .. Cas 2 : quel est l'état mécanique d'équilibre final de la barre ? Justifier. Le poids de la tige et l'action de l'axe sur la barre passent par O : ces forces ont un moment nul par rapport à O. Cas 3 : quel est l'état mécanique d'équilibre final de la barre ? Justifier. On pose OM2 = d. A l'équilibre a = 90°. . Balance romaine. L'équilibre est réalisé grâce à un contre-poids coulissant appelé peson. Le corps principal de la balance est constitué d'une pièce métallique dont la forme permet d'identifier deux bras. - Le fléau gradué correspond au bras fin et allongé sur lequel peut coulisser le peson. Une simple lecture indique la masse qui est à peser. - La tête correspond au bras élargi et plus court de la balance. La balance est suspendue du côté de la tête grâce à un anneau. La masse à peser y est acrochée. Deux anneaux de suspension permettent d'effectuer deux types de mesures. Of est le point de contact avec la balance romaine de l'anneau de suspension côté faible. OF est le point de contact avec la balance romaine de l'anneau de suspension côté fort. Oc et O'c sont respectivement les points de contact du crochet à peser avec la balance suivant qu'elle utilise l'anneau de suspension respectivement côté faible ou côté fort. Amax et A'max sont respectivement les positions les plus éloignées de la tête que peut atteindre le peson sur le fléau avec une balance suspendue par l'anneau respectivement côté faible et côté fort. G correspond au centre de masse du corps principal de la balance comme le point de l'espace où s'applique le poids de la balance. On suppose dans la suite que G est situé sur la droite verticale pasant par Of lorsque la balance est à l'équilibre horizontal. mb : masse du corps de la balance ; mc : masse du crochet de pesée ; mp : masse du peson. OfOc = lc ; OfA = lp ; OfAmax = lM ; OfG = L. Quel peut être l'intérêt d'utiliser la balance romaine dans l'un ou l'autre des deux sens, c'est à dire en la suspendant par l'un ou l'autre des deux anneaux ? Par retournement du fléau, on privllégie la précision ( anneau de suspension côté faible) ou la pesée de masse importante ( anneau de suspension côté fort). Dans la suite du problème, on s'intéresse uniquement au cas où la balance est suspendue par l'anneau côté faible ( on considère qu'i n'y a pas d'anneau côté fort ). Lensemble du système sera considéré comme plan. La modélisation de la balance est simplifiée. La balance peut pivoter autour de l'axe Ofz. Montrer que le moment en Of de la réaction de l'anneau de suspension sur la barre est toujours nul. La réaction de l'anneau de suspension sur la barre rencontre l'axe de rotation. Le bras de levier est nul. Le moment en Of de cette force est nul. Etude de l’équilibre mécanique de la balance pour m = 0. Nous allons à présent décrire une séquence de pesée d’un objet de masse m inconnue et fixé sur le crochet de pesée. Le protocole de mesure de m commence par étudier l’équilibre de la balance « à vide », c’est-à-dire lorsqu’aucune masse n’est fixée sur le crochet de pesée : m = 0. On étudie plus particulièrement l’équilibre horizontal de la balance pour lequel l’angle θ de la balance avec l’axe (Of x) est nul. On note dans ces conditions A0 la position correspondante du peson sur le fléau. Etablir l’expression de ℓ0 = ℓp(m = 0) = OfA0 en fonction de ℓc, mc et mp. G est sur la verticale de l'axe de rotation : le moment de Pb par rapport à Of est nul. A l'équilibre : mc ℓc =ℓ0 mp soit ℓ0 = mc ℓc / mp. Etude de l’équilibre mécanique de la balance pour m différent de zéro. On poursuit le protocole de mesure en accrochant la masse m inconnue au crochet de pesée. A quel cas de la figure 2 cette situation se rapproche-t-elle le plus ? Cas n°3. Dans quel sens doit-on déplacer le peson si l’on souhaite retrouver une situation d’équilibre horizontal de la balance ? On repérera à présent la position du peson grâce à la distance ℓ définie par lp = l0 +l. On déplace le peson vers la droite. On souhaite retrouver un état d’équilibre de la balance pour un angle qéq quelconque. L’objectif est de déterminer l’expression de la longueur l en fonction de la masse m. Déterminer l’expression de l’angle qéq en fonction de m, mp, mb, L, lc et l en appliquant la loi du moment cinétique à l’équilibre. 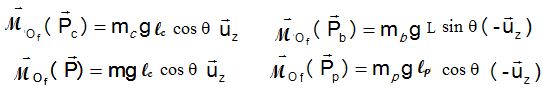A l'équilibre : ( (m+mc )ℓc - ℓp mp) cos qéq = mb Lsin qéq . tan qéq  = ( (m+mc )ℓc - ℓp mp) / (mb L).  Quelle relation vérifie ℓ, ℓc, mp et m si on ramène qéq à une valeur nulle ? (m+mc )ℓc = ℓp mp ; ℓp =l0 +l=(m+mc )ℓc /  mp ; l= (m+mc )ℓc /  mp -l0 = mℓc /  mp.  En déduire le principe de fonctionnement de la balance romaine. On explicitera notamment dans le détail un protocole permettant de graduer le fléau pour réaliser la conversion "longueur - masse". La masse m est proportionnelle à la longueur l. On recherche un équilibre avec la tige horizontale. m=0, repèrer la position du peson l0, origine de la graduation. Accrocher des masses connues ( 200, 500, 1kg, 1,5 kg...), déplacer le peson pour réaliser l'équilibre et repérer sa position. Pendant très longtemps, la balance romaine a été préférée aux balances à plateaux par les maraîchers. Proposer une justification à ce choix. Simple d'emploi, robuste, ( on ne risque pas de perdre les masses marquées) et les pesées peuvent s'étaler de quelques centaines de grammes à plusieurs kilogrammes.  On appelle sensibilité, notée S, la variation de position du peson par unité de masse ajoutée au crochet de pesée. Etablir l’expression de la sensibilité en fonction de lc et de mp. l=mℓc /  mp ; l/m =S=ℓc /  mp . Quelle est l’expression de la portée M de la balance, valeur maximale de masse m qui peut être mesurée sur cette balance ? On exprimera le résultat en fonction de mp, mc, lM et lc. lM : longueur du fléau ; lM -ℓ0 =M ℓc /  mp ; ℓ0 = mc ℓc / mp ; lM = ℓc / mp ( M + mc). M = lM  mp /  ℓc -mc. En déduire l’expression de la sensibilité S en fonction de M, mc et lM. S=ℓc /  mp  =lM / ( M + mc). On souhaite fabriquer, côté faible, une balance d’une portée de 5, 00 kg. On souhaite pour cela utiliser un fléau de longueur lM = 50, 0 cm, un peson de mp = 500 g et un crochet de masse mc = 100 g. Déterminer les valeurs de ℓc et de ℓ0 correspondant à une telle balance. ℓc =lM mp / ( M + mc) =0,500 *0,500 / 5,10=0,0490 m = 4,90 cm. Déterminer la sensibilité de cette balance. On exprimera le résultat en cm.kg−1. S= lM / ( M + mc) = 50,0 / 5,10 =9,80 cm.kg−1. On suppose à présent que la balance a été conçue de manière à ce que la position ℓ0 corresponde à un peson en butée contre la tête de la balance. On s’intéresse, pour ces dernières questions, au côté fort de la balance précédente en retournant cette dernière pour la suspendre par le second anneau. On appelle J le point d’intersection de la droite (OfG) et du segment [OFA′max] et on note dans ce cas d = OF J. On donne mb = 250 g. On souhaite disposer côté fort d’une portée M′ = 20, 0 kg. Faire un schéma de la situation puis déterminer l’expression de d en fonction de ℓc, ℓM, mc, mp, mb et M′. On supposera qu’il n’y a pas d’anneau de suspension coté faible et on se limitera au cas où l’angle θ de la balance avec l’horizontale est nul. Calculer la valeur de d. 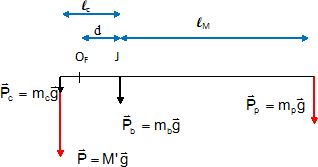A l'équilibre : (mc +M')(lc -d)=mbd +mp(d+lM) ; d=((mc +M')lc -mplM) ) / (mb+mp+mc +M'). d=(0,100+20,0)*0,0490-0,50*0,50) / (0,25+0,50+0,10+20,0)=0,0354 m ~ 3,54 cm. Quelle est la masse minimale que l’on peut mesurer côté fort ? Le peson est pratiquement en J : à l'équilibre : (mc +Mmini)(lc -d)=(mb +mp)d ; Mmini =(mb +mp)d) / (lc -d) - mc= 0,75 *0,0354 / 0,0136 =1,95 ~ 2,0 kg.  La sensibilité de la balance est-elle meilleure côté fort ou côté faible ? S= lM / ( M' + mc) = 50,0 / 20,10 =2,5 cm.kg−1. La sensibilité de la balance est plus faible côté fort.

menu