Principe d'équivalence fort, gravitation artificielle. Concours général 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Les vecteurs sont écrits en gras et en bleu. Une force d'inertie est une force apparente qui agit sur un corps lorsque le mouvement de celui-ci est étudié dans un référentiel accéléré par rapport à un référentiel galiléen. L'impesanteur est-elle l'absence de poids ? Justifier. L'impesanteur n'est pas l'absence de poids ; l'impesanteur est ressentie lorsque l'accélération subie égale la gravité. On considère un individu de masse m = 60 kg dans une fusée en accélération uniforme par rapport à un référentiel supposé galiléen. Sachant que cet individu pèse 220 N dans  la fusée, s'il lâche un marteau dans la cabine d'une hauteur de 1,0 m, quelle serait la durée de la chute ? Accélération subie a = 220 / 60 =3,67 m s-2. Chute verticale sans vitesse initiale : z = ½at2 ; t =(2z / a)½ =(2,0 / 3,67)½ ~0,74 s. Dans certains films de science-fiction, on peut voir des vaisseaux spatiaux en forme de roue dont le mouvement de rotation autour de leur axe induirait une gravité artificielle semblable à celle de la terre. On considère une roue de 120 m de rayon,dont le centre est en mouvement rectiligne uniforme dans un référentiel supposé galiléen, quelle devrait être la période de rotation de ce vaisseau pour générer un champ gravitationnel artificiel semblalble à celui de la terre ?  g = w2 r  avec w vitesse angulaire en rad/s, r : rayon de la roue. w = (g / r)½ =(9,8 /120)½=0,286 rad/s ; T = 2p / w = 6,28 / 0,286 ~22 s. On souhaite que les électrons soient déviés vers le bas. Préciser le sens du champ gravitationnel ainsi créé.. L'accélération est centripète..   Enoncé du principe d'équivalence fort. Le principe d'équivalence induit que les effets d'un champ gravitationnel sur une expérience de mécanique sont identiques aux effets d'une accélération du référentiel de l'observateur. 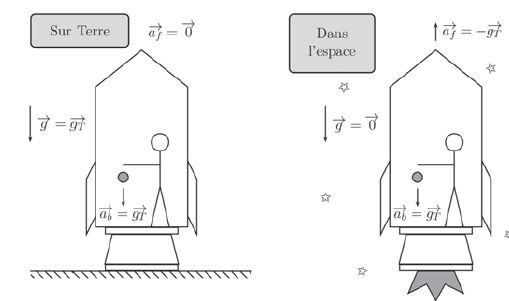On prend ici l'exemple d'un individu lâchant une balle dans une fusée au repos sur terre, soit en accélération uniforme, d'intensité égale à l'accélération de la pesanteur. On note g le champ gravitationnel extérieur, gT celui de la terre à sa surface, ab et af les accélérations respectives de la balle par rapport au référentiel de la fusée et de la fusée par rapport au référentiel terrestre supposé galiléen. .. .. Déplacement d'un ballon dans une voiture. On considère une voiture initialement au repos. On fixe par l'intermédiaire de deux ficelles, respectivement à son plancher et à son plafond, deux ballons de baudruche remplis respectivement d'hélium et de dioxyde de carbone gazeux. La voiture ainsi préparée démarre et conserve une accélération constante pendant un certain temps. Quelle est la ficelle la plus inclinée ? De quel angle s'incline-t-elle ? Discuter de l'accélération nécessaire pour observer un effet significatif. Ballon rempli de CO2 suspendu au plafond. me : masse de l'enveloppe ; V : volume du ballon ; rg masse volumique du gaz ; rair : masse volumique de l'air. Le ballon est soumis : à son poids verticale vers le bas, valeur (me +rg V)g = m'g  à la poussée d'Archimède due à l'air, verticale, vers le haut, valeur rair Vg  ;  à la tension du fil. Le ballon étant immobile, on fait intervenir une force d'inertie -m'a avec a : accélération du véhicule. Poids apparent du ballon = poids - poussée = (me +(rg -rair )V)g  = m g. 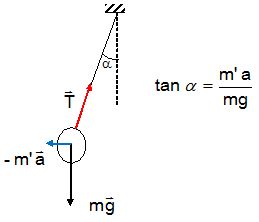Dans l'hypothèse où la masse de l'enveloppe et la poussée sont négligeables et pour un angle de 10°, a = 9,8 tan 10 = 1,7 m s-2. . 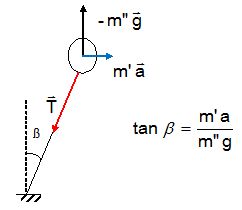Ballon d'hélium relié au sol. L'hélium est un gaz plus léger que l'air. Lors d'une accélération, l'air se déplace vers l'arrière et repousse le ballon d'hélium vers l'avant. me : masse de l'enveloppe ; V : volume du ballon ; rg masse volumique du gaz hélium ; rair : masse volumique de l'air. Le ballon est soumis : à son poids verticale vers le bas, valeur (me +rg V)g = m'g  à la poussée d'Archimède due à l'air, verticale, vers le haut, valeur rair Vg  = m"g  à la tension du fil. Le ballon étant immobile, on fait intervenir une force d'inertie m'a avec a : accélération du véhicule. La poussée l'emporte sur le poids. Dans l'hypothèse où la masse de l'enveloppe et le poids de l'hélium sont négligeables  devant la poussée et pour un angle de 10° :  a = rair / rg 9,8 tan 10 = 1,7 m s-2avec rair / rg ~1,2 / 0,2 ~6. a ~6*9,8*tan10 ~10 m s-2. Pour une même accélération, le pendule au ballon d'hélium est le moins dévié. . .

menu