Principe
d'équivalence faible, particule chargée dans un champ électrique, chute
verticale.
Concours général 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Les vecteurs sont
écrits en gras et en bleu.
La masse inertielle mesure la "résistance" à toute variation de
son mouvement. Elle apparaît dans la relation fondamentale de la
dynamique.
Enoncer le principe d'inertie.
Dans un référentiel
galiléen, le centre d'inertie d'un solide pseudo-isolé est soit au
repos ( si la vitesse initiale est nulle) soit animé d'un mouvement
rectiligne uniforme.
Décrire une expérience simple qui illustre le principe d'inertie.
Lancer d'un mobile sur une table à coussin
d'air horizontale.
On
considère la situation suivante dans laquelle nous allons comparer les
forces nécessaires pour modifier le mouvement d'un électron de masse me
et d'un proton de masse mp. De sélectrons de vitesse
initiale v0 = v0
ux avec v0
= 1,5 107 m/s, pénètrent en un point O dans une zone de
l'espace située entre les armatures planes et horizontales d'un
condensateur. Il règne dans cette zone un champ électrique uniforme E et de
valeur E = 6,0 kV / m.
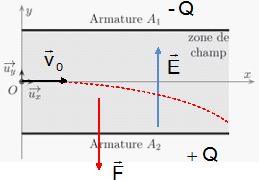
On souhaite que les électrons soient
déviés vers le bas.
Montrer que l'effet du poids de l'électron est négligeable devant
l'effet de la force électrostatique à laquelle il est soumis.
P =meg
= 9,1 10-31*9,8 ~8,9 10-30
N ; F = e E = 1,6 10-19 *6,0 103
=9,6 10-16 N. P << F.
Donner l'expression
vectorielle de l'accélération de l'électron et calculer sa valeur.
F = -e E = me a ; a = -e / me E.
|a|=1,6 10-19
/ (9,1 10-31) * 6,0 103
= 1,055 1015 ~1,1 1015
m s-2.
Quelle est l'armatrure chargée positivement ? Justifier. On notera Q sa
charge.
Les électrons sont déviés
vers le bas ; la force à laquelle ils sont soumis est verticale vers le
bas. le champ électrique est vertical vers le haut ; l'armature A1
est négative ; l'armature A2 est positive.
Etablir les équations horaires du mouvement de l'électron dans le
condensateur.
ax
=0 ; ay = -e / meE;
az
=0.
vx =v0 ; vy = -e / meE t ; vz =0.
x = v0
t ; y = -½e / meE t2 ; z =0.
Interpréter pourquoi la vitesse de l'électron selon l'axe (Ox) est
constante.
La seule force agissant
sur l'électron est verticale. Suivant Ox, l'électron est isolé ;
d'après le principe d'inertie, son mouvement est rectiligne uniforme.
Montrer que la trajectoire de l'électron est parabolique.
y = -½e / meE x2 /v02;
équation d'une branche de parabole.
Reproduire
le schéma du condensateur accompagné des grandeurs suivantes : charges
des armatures, champ E, force F,
trajectoire de l'électron. Voir ci dessus.
|
| ..
.. |
|
|
On souhaite maintenant étudier le
mouvement d'un proton dans ce condensateur. Le proton pénètre dans la
zone de champ en O dans les mêmes conditions que l'électron.
Quelles précautions faut-il prendre pour que le proton ait exactement
la même trajectoire que celle de l'électron précédent ? Calculer la
valeur de la grandeur qui doit être modifiée.
Il faut d'abord inverser
le sens de la tension électrique, ca qui revient à inverser le sens du
champ électrique. Il faut modifier la valeur du champ électrique :
e / meE = e /mp E' ; E' = mp/ meE
= 1,6 10-27 /(9,1 10-31) *6,0 ~ 1,1 104
kV / m.
On suppose que l'on est en mesure d'introduire
un second proton au point J, de coordonnées ( xJ ; 0 ; 0 )
avex xJ >0 et on le lâche sans vitesse initiale au moment
où l'on introduit un premier proton en O à la vitesse v0. On
négligera l'interaction entre les deux protons vis-à-vis de
l'interaction de chacun d'eux avec le champ.
Le second proton atteindra-t-il l'armature inférieure avant, après ou
en même temps que le proton introduit en O ? Justifier. On note avec d la demi distance des plaques.
Proton introduit en O : x = v0 t ; y = -½e / mpE t2 ; z =0.
Ce proton atteint la plaque inférieure à
la date t = [2dmp
/(eE)]½ .
Proton
introduit en J : x = xJ ; y = -½e / mpE t2 ; z =0. Ce proton
atteint la plaque inférieure à la date t = [2dmp
/(eE)]½ .
Ces protons étant soumis à la même force verticale, atteindront la
plaque inférieure à la même date.
|
.
|
|
La
masse gravitationnelle est la grandeur physique intervenant dans la loi
de l'attraction gravitationnelle.
Quel physicien a découvert la loi de gravitation universelle ? Isaac Newton.
Pourquoi dit-on que cette loi est universelle ?
Cette loi décrit
l'attraction des corps ayant une masse, que ce soit la chute des corps
ou le mouvement des corps célestes.
Comment se compare t-elle aux autres interactions fondamentales ? Dans
quelles situations est-elle prépondérante ?.
La
gravitation est prépondérante dans l'infiniment grand ( mouvement des
étoiles, panètes et galaxies ). Elle est toujours attractive, est
proportionnelle aux masses et varie en raison inverse du carré de la
distance séparant deux corps.
Calculer la valeur de l'intensité du champ gravitationnel à la surface
de la terre puis à la surface de la lune.
gT
= G MT / RT2
=6,674 10-11*5,9736 1024
/(6,371 106)2 =9,822 m s-2.
gL
= G ML / RL2
=6,674 10-11*7,347 1022
/(1,736 106)2 =1,627 m s-2.
Universalité
de la chute libre. Le principe d'équivalence faible dit que la
masse inertielle et la masse gravifique sont égales quel que soit le
corps. En conséquence,
deux corps lâchés au même endroit et soumis uniquement à l'influence du
champ gravitationnel suivent exactement la même trajectoire, même s'ils
ont des compositions différentes.
Galilée est un des premiers physiciens
ayant étudié le mouvement de la chute des corps du haut de la tour de
Pise.
Aristote déclare qu'un boulet de fer de 100 livres est déja
descendud'une hauteur de 100 coudées quand un boulet de 1 livre a
parcouru seulement une coudée. Galilée affirme que les deux boulets
arrivent ensemble. des expériences répétées montrent qu'un boulet de
100 livres met 5 s pour desendre de 100 coudées.
Une coudée correspond à 57 cm et une livre à 339,542 g. On prendra rfer = 7,87 103
kg m-3.
Calculer la masse des boulets de fer évoqués ci-dessus.
100 livres = 100 *339,542
=33,9542 kg ; 1 livre = 0,339542 kg.
Calculer le rayon de chaque boulet de fer.
m=rfer *4/3 pR3 ; R =[
3 m /(4rfer
p)]1/3
=[3*33,9542/(4*7,87 103*3,1416)]1/3 =0,1001 m
pour le boulet de 100 livres.
R =[ 3 m /(4rfer
p)]1/3
=[3*0,339542/(4*7,87 103*3,1416)]1/3
=2,176 10-2 m pour le boulet de 1 livre.
Etablir l'équation horaire du mouvement de la chute libre des boulets
de fer.
On choisit un axe
vertical orienté vers le bas, l'origine étant l'altitude initiale
H des boulets. La vitesse initiale est nulle.
a = g ; v = gt ; z = ½gt2.
Sur un axe gradué, placer et numéroter les positions successives du
boulet tous les t
= 0,5 s.
t(s)
|
0
|
0,5
|
1
|
1,5
|
2
|
2,5
|
3
|
3,5
|
z(m)
|
0
|
1,2
|
4,5
|
11,0
|
19,6
|
30,6
|
44,1
|
60,0
|

|
Calculer Dt,
la durée de chute du haut des 100 coudées et conclure.
100 coudées = 100 *0,57 = 57 m ; Dt
=(2z/g)½ =(2*57 /9,8)½ =3,4 s.
La chute d'un
boulet de 100 livres n'est pas libre ( durée de la chute mesurée 5 s).
Le boulet est soumis à d'autre forces que son poids : esentiellement
frottements sur les couches d'air ; la poussée d'Archimède due à
l'air est négligeable.
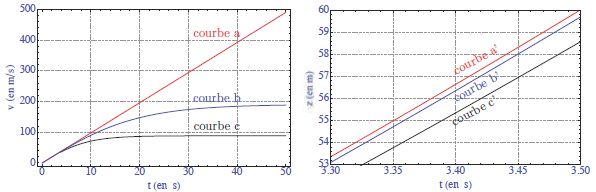
Les graphes suivants représentent différentes simulations associées à
la chute de chacun des types de boulets, respectivement de masse 100
livres et une livre.
|
|
|
|
Sans souci d'échelle, représenter les
forces qui s'exercent sur le boulet lors de sa chute dans l'air.
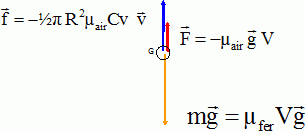
Montrer que la poussée
d'Archimède est négligeable devant les autres forces.
mg
/ F =µfer / µair = 7,87 103 /1,29 = 6,10 103. La poussée est bien
néglieable devant le poids.
Montrer
qualitativement que le boulet peut atteindre un mouvement
rectiligne uniforme.
Lorsque le poids est
compensé par les forces de frottement dues à l'air, le boulet est
pseudo-isolé. Le principe d'inertie indique que le mouvement devient
rectiligne uniforme.
Exprimer puis calculer la vitesse limite vl de chute. On
prendra C = 0,44.
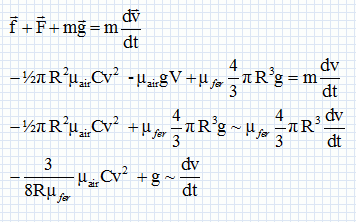 |
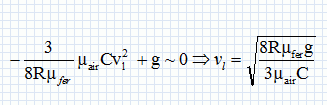
vl
=(8*0,10*7,87 103*9,8 / (3*1,29*0,44))½
=191 ~1,9 102 m/s. ( boulet de 100 livres)
vl =(8*2,18 10-2*7,87 103*9,8 /
(3*1,29*0,44))½
=88,9 ~89 m/s. ( boulet de 1 livre)
|
Attribuer chaque courbe a, b, c de la
simulation au cas qui convient.
a : chute libre ; b :
chute du boulet de 100 livres ; c : chute du boulet de une livre.
Les graphes z = f(t) de
la simulation montrent un désaccord avec un résultat énoncé par Galilée
( la chute ne dure pas 5 s ).
Par contre " deux
boulets arrivent ensemble" est confirmé ( écart de 0,03 s).
Pour montrer que la chute des corps est indépendante de la masse de
l'objet, que vaut-il mieux choisir comme objets ?
Des objets de même taille
mais de compositions différentes.
Comme les objets tombaient trop rapidement pour permettre des mesures
directes, Galilée eut l'idée brillante de "diluer la gravité" en
faisant rouler des boules sur un plan légèrement incliné. Ses études
lui on permis de conclure que la distance totale augmente comme le
carré du temps écoulé.
Que signifie " diluer la gravité" ?
Sur un plan incliné, le
boulet est soumis à l'accélération g sin ß, avec ß inclinaison du plan
par rapport à l'horizontale. Si ß =5°, gsin 5 =0,087 g.
En 1971, l'expérience de la chute des corps fut refaite par
l'astronaute David Scott, sur la lune. Il lâcha une plume et un
marteau au même insatnt ; des millions de téléspectateurs furent ainsi
témoins que les deux objets arrivaient en même temps au sol.
.
|
|
|