Diffraction, transfert thermique, satellite, saut à ski. Concours Ecole Nationale Supérieure Maritime 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Diffraction.( 5 points) On réalise une expérience de diffraction à l'aide d'un laser émettant une lumière monochromatique de longueur d'onde l (figure 1). À quelques centimètres du laser, on place successivement des fils verticaux de diamètres connus. On désigne par "a" le diamètre d'un fil. La figure de diffraction obtenue est observée sur un écran blanc situé à une distance D = 2,00 m des fils. Pour chacun des fils, on mesure la largeur L de la tache centrale. À partir de ces mesures et des données, il est possible de calculer l'écart angulaire q du faisceau diffracté. 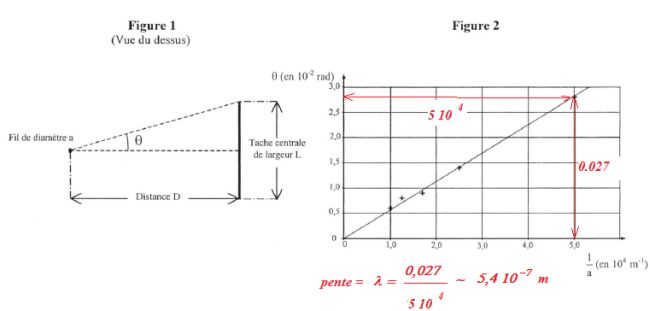1. Donner la relation entre L et D qui a permis de calculer q pour chacun des fils. tan q = ½L / D ~q pour les petits angles. 2. Donner la relation liant q, l et a. Préciser les unités. q = l / a. q (radian) , l et a en mètres. La courbe q =f (1/a) est donnée sur la figure 2. 3. Montrer que la courbe obtenue est en accord avec l'expression de q donnée à la question 2.  q est proportionnel à l'inverse du diamètre des fils. La constante de proportionalité est égale à la longueur d'onde l. La courbe q =f (1/a) est une droite passant par l'origine. 4. Déterminer, à partir de la courbe, la longueur d'onde l de la lumière monochromatique utilisée. 540 nm. Si l'on réalisait la même étude expérimentale en lumière blanche, on observerait des franges irisées. 5. Justifier l'aspect «irisé» de la figure observée en utilisant la relation de la question 2. Chaque radiation de la lumière polychromatique donne un système de diffraction dont la largeur de la tache centrale est proportionnelle à la longueur d'onde. Au centre de la tache toutes les radiations sont présentes ( couleur blanche) ; le bord de la tache centrale est orange-rouge, le bleu étant absent. Transfert thermique. ( 5 points) On désire chauffer l'eau d'une tasse à l'aide d'un four à micro-ondes. Lorsque les micro-ondes atteignent les molécules d'eau, elles se mettent à osciller 2,45 109 fois par seconde. la mise en mouvement des molécules d'eau produit la chaleur nécessaire pour chauffer l'eau. Puissance du micro-ondes P = 750 W ; capacitée thermique de l'eau ceau =4180 J kg-1 K-1 ; volume de la tasse V = 33 cL ; température initiale de l'eau : Ti = 18°C ; température finale de l'eau Tf = 90°C. 1. Indiquer à quel type d'ondes les micro-ondes appartiennent. Les micro-ondes font partie des ondes électromagnétiques. 2. Déterminer la longueur d'ondes des micro-ondes du four. l = c / f = 3,00 108 / (2,45 109)=0,122 m. 3. Calculer la variation de l'énergie interne de l'eau contenue dans la tasse. DU = m ceau(Tf-Ti) avec m = 0,33 kg. DU =0,33 *4180(90-18)=9,9 104 J. 4. Déterminer combien de temps il faudra pour chauffer la tasse d'eau. t = DU  / P = 9,9 104 / 750 =1,3 102 s. . . Satellite( 5 points). Le GPS (Global Positioning System) comporte une trentaine de satellites en orbites quasi-circulaires faisant deux révolutions par jour autour de la Terre. Chaque satellite émet un signal électromagnétique dirigé vers la Terre. Données : Célérité de la lumière dans le vide ……….c = 3,00 × 108 m.s-1 Altitude moyenne des satellites GPS ……h = 2,00 × 104 km Masse de la Terre …………………………M = 5,98 × 1024 kg Rayon de la Terre …………………………R = 6,37 × 103 km Constante de gravitation universelle ……G = 6,67 × 10-11 m3.kg-1.s-2 Le mouvement du satellite est étudié dans le référentiel géocentrique supposé galiléen. 1. Donner les caractéristiques d’un référentiel géocentrique. Les comparer avec celles d’un référentiel terrestre. Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes. Le référentiel géocentrique a pour origine le centre de la Terre et des axes parallèles à ceux du référentiel héliocentrique. Le référentiel terrestre est centré sur le centre de masse de la terre et les trois axes sont liés au globe terrestre. 2. Montrer que le mouvement d’un satellite GPS de masse m est uniforme en supposant que son orbite est circulaire. Le satellite est soumis uniquement à la force centripète de gravitation de la terre. Cette force, constamment perpendiculaire à la vitesse, ne travaille pas. En conséquence l'énergie cinétique et la vitesse du satellite ne varient pas. Le mouvement est donc uniforme. 3. Montrer que l’expression de la vitesse du satellite est v =(GM/(R+h))½ et déterminer sa valeur numérique. On pose r = R+h. 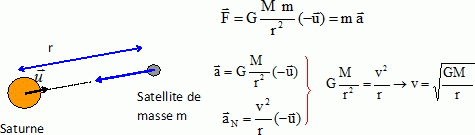r = 6,37 × 106 + 2,00 107 =2,637 107 m. v = (  6,67 10-11*5,98 1024 / (2,637 107))½ =3,89 103 m /s. 4. Établir l’expression de la période de révolution d’un satellite GPS. Calculer sa valeur et vérifier qu’elle est compatible avec l’information du texte d’introduction. Le satellite décrit la circonférence 2pr à la vitesse v en T seconde. T = 2pr  / v = 6,28 *2,637 107 / (3,89 103) =4,26 104 s ou  environ 12 h. 5. Justifier par le calcul la phrase suivante : « Pour bénéficier d’une précision de 10 m dans la direction de propagation du signal électromagnétique envoyé par un satellite GPS, le récepteur GPS doit mesurer la durée de trajet de ce signal avec une précision d’environ 30 ns. » 10 / (3,00 108) = 3,3 10-8 s = 33 ns. 6. Déterminer la durée de parcours du signal électromagnétique. En déduire la précision relative sur la mesure de cette durée. 2 107 / (3,00 108) =6,66 10-2 s.  30 10-9/ (6,66 10-2 ) =4,5 10-7. Tremplin de saut à ski. 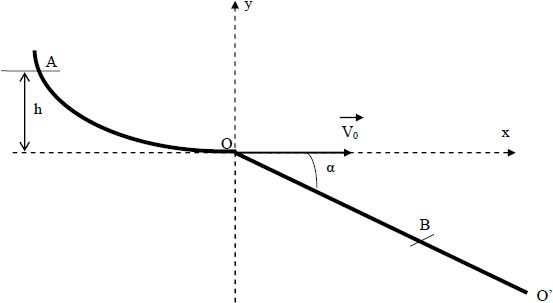(5 points) Le tremplin est constitué d’une piste d’élan AO de profil curviligne et d’une piste de réception OO’ plane et inclinée d’un angle a par rapport à l’horizontale. Le skieur de masse m est assimilé à un point matériel noté G. Les frottements sont supposés négligeables et le référentiel terrestre supposé galiléen. Le mouvement du skieur s’effectue dans le plan vertical (xOy). Le skieur part du point A sans vitesse initiale et en O sa vitesse, de valeur V0, est horizontale. Données : h = 50,0 m ; m = 80 kg ; g = 9,81 m.s-2 ; a = 30°. 1. Etablir l’expression littérale de V0 en fonction de g et h. Calculer sa valeur. Le skieur est soumis à son poids et à l'action du plan perpendiculaire au plan ( cette force ne travaile pas). Travail moteur du poids entre A et O :mgh. Théorème de l'énergie cinétique entre A et O : ½mv2O -0 = mgh ; VO = (2gh)½ . VO=(2*9,81*50,0)½=31,32 ~31,3 m/s. 2. Etablir l’équation cartésienne de la trajectoire du skieur après qu’il ait quitté la piste en O. Accélération : ax=0 ; ay=-g ; vitesse : vx=vo ; vy = -gt. Position x = vot ; y =-½gt2. Trajectoire : y = -½gx2/v2o.  3. Donner l’équation de la partie linéaire OO’ de la piste de réception en utilisant tan a. y = -tan a x. 4. Déterminer les coordonnées xB et yB du point B où le skieur reprend contact avec la piste. -½gxB2/v2o = -tan a xB. xB =2tan a v2o /g = 2 tan 30 *31,322 / 9,81 = 115,46 ~115 m. yB = -tan 30 *115,46 =-66,66 ~ -66,7 m. 5. Déduire des coordonnées la longueur L = OB du saut. L = (x2B +y2B)½ =(115,462 +66,662)½~133 m. 6. Calculer la durée du saut. t = xB / vo =115,46 / 31,32 =3,69 s. .

menu