Mathématiques. Concours
Ecole
Nationale Supérieure Maritime 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Question 1.( 2points)
1. Déterminer l’ensemble des solutions dans R de l’équation différentielle y'+½y=0.
Solution du type y = A exp(-0,5x) avec A une constante.
2. Déterminer l’ensemble des solutions dans R de l’équation différentielle 2y'+ y - 4 = 0.
Solution de l'équation sans second membre 2y'+y=0.
y=A exp(-0,5x) avec A une constante.
Solution particulière de l'équation différentielle : y = 4.
Solution générale de l'équation différentielle : y=A exp(-0,5x) +4..
Question 2. ( 1,5 points)
Soit
X la variable aléatoire correspondant à la durée de vie, en heures,
d’un appareil. On suppose que X suit une loi exponentielle de paramètre
l=10-2.
1. Donner la densité de probabilité de X.
f(x) = l e(-lx) = 0,01 e(-0,01x) pour x positif ou nul.
f(x)=0 pour x négatif.
2. Calculer la probabilité P(X ≤ 200) au dixième près. (On pourra considérer e≈3).
P(X ≤ 200) =1-e(-0,01x)=1-e(-0,01*200) = 1-e(-2) ~1-1/9 ~0,9.
Question 3.
(2 points)
Une personne dispose d’une pièce de monnaie. Elle souhaite savoir si sa pièce est équilibrée,
c’est-à-dire si la probabilité d’obtenir « pile » est égale à 0,5.
Pour effectuer cette vérification, elle lance successivement 100 fois
la pièce. Elle obtient 20 fois « pile » et 80 fois « face ».
1. Calculer l’intervalle de confiance de p au seuil de 95%, où p est la probabilité (inconnue) d’obtenir « pile ».
[p -1/n½ ; p+1/n½] avec n = 100 et n½ = 10 et p = 0,2.
[0,1 ; 0,3].
2. Peut-on conclure, avec un risque d’erreur de 5%, que la pièce est équilibrée ?
Avec un seuil de confiance de 95 %, on obtiendra entre 10 et 30 fois pile sur 100 lancers.
Pour une pièce équilibrée, les probabilités d'obtenir pile ou face sont identiques. La pile n'est pas équilibrée.
Question 4 ( 4,5 points).
Le plan complexe est muni d’un repère orthonormal direct (O ; u,v) d’unité graphique 1 cm.
On considère le nombre complexe suivant : z = - 1+ i
1. Déterminer le module z .
|z| = ((-1)2 +12)½ =2½~1,414.
2. Ecrire le complexe conjugué de z, 1/z, z2/2½ et -z sous forme algébrique.
Conjugué de z : -1-i ; 1/z = 1/(-1+i) = (-1-i) / [(-1+i)(-1-i)]=(-1-i) / 2.
z2/2½ =2 / 2½ = 2½. -z = 1-i.
3. On appelle A, B et C les points d’affixes respectives z, z2/2½ et -z
Déterminer AB2, BC2 et AC2. En déduire que le triangle ABC est rectangle en B.
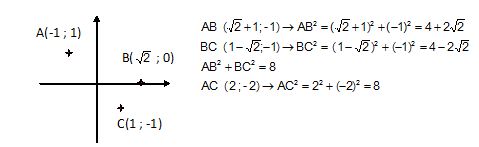
Le théorème de Pythagore étant vérifié, le triangle ABC est rectangle en B.
|
| .
. |
|
|
Question 5 ( 7 points).
Soient f et g les fonctions définies sur l’intervalle ]0 ;+oo[ par f(x) =1+ln(x) / x et par
g(x) = (ln x)2 .
1. Déterminer la limite de f en + oo .
La limite de ln(x) / x est égale à zéro si x tend vers l'infini et celle de f(x) est donc égale à 1.
2. Calculer la dérivée de f et donner le tableau de variation de f .
On pose u = ln(x) et v = x ; u' = 1/x et v'=1.
Dérivée d'un quotient (u'v-v'u ) / v2 = (1-ln(x) ) / x2 ; f '(x) = (1-ln(x) ) / x2 .
La dérivée s'annule pour ln(x)=1 soit x = e.
La dérivée est positive pour x <e et négative pour x >e.

3. Calculer f(1) et ) f(e) . En déduire l’encadrement de 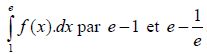 . .
f(1) =1 ; f(e) = 1+1/e.
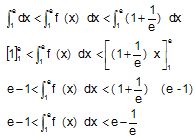
4. Déterminer la dérivée de g . Exprimer f en fonction de g’. En déduire la valeur exacte
de 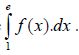
On pose u = ln(x) ; u' = 1/x ; g = u2 ; g'= 2uu' = 2ln(x) / x .
f(x) = 1+½g'(x).
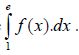 =[ x]1e +½[g(x)]1e =e-1+½(12)=e-½. =[ x]1e +½[g(x)]1e =e-1+½(12)=e-½.
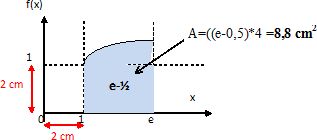
5. On appelle D l’ensemble des points M de coordonnées x et y vérifiant 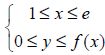
dans un plan muni d’un repère orthonormal (O ;u,v) d’unité graphique 2 cm.
Calculer au dixième près l’aire, en cm2, du domaine D. (On pourra considérer e≈2,72).
|
|
|
|
Question 6. (3 points)
. On considère la suite un pour n positif ou nul, définie par le réel u0 et la relation de récurrence
un+1=11 un -10 pour tout entier naturel n .
1. Déterminer u0 pour que la suite soit constante.
Tous les termes doivent être identiques : u1 = 11u0 -10 = u0 soit u0 = 1.
2. On choisit u0 = 2.
Montrer que la suite vn définie par vn = un-1 pour tout entier naturel n est une suite géométrique de raison q =11.
Exprimer vn en fonction de n , puis calculer v0+v1+v2+K + v10. (On pourra considérer 1110≈2,6 1010).
u0 = 2 ; u1 =12= 11+1 ; u2 = 122 = 121+1 = 112+1 ; u3 = 1332= 1331+1 = 113+1 ; .... un =11n+1.
v0 = 1 ; v1 =11 ; u2 = 121 = 112 ; u3 = 1333 = 113; .... vn = 11n ; vn+1 =11 un -1 = 11n+1.
v0+v1+v2+K + v10 = premier terme (1-qnombre de terme) / (1-q).
v0(1-q11) / (1-q) =(1-1111) / (-10)~(11*2,6 1010-1) / 10 ~2,8 1010.
|
|
|
|