Le phénomène de sédimentation. Concours national Deug . . . . Les vecteurs sont écrits en gras et en bleu. Un récipient cylindrique de  section droite d'aire S et d'axe vertical ascendant Oz ( vecteur unitaire ez ), contient un liquide homogène incompressible de masse volumique r. l'origine O est choisiie au fond du récipient : z(O) = 0. Des macromolécules insolubles, notées M, de forme sphériques ( rayon R, masse m )  et de masse volumique r0 ( avec r0 > r), sont ajoutées et mélangées au liquide. Au temps initial t=0, la solution supposée homogène, est abandonnée à elle même : les macromolécules se déposent, à la vitesse v, sous l'action des forces de pesanteur ( sédimentation). En plus de leur poids P = -mgez, les particules M sont soumises à deux autres forces : une force de frottement visqueux, dite de Stokes, de la forme Ff=-fv (avec f constante positive ) et la poussée d'Archimède FA = 4/3pR3 rgez. 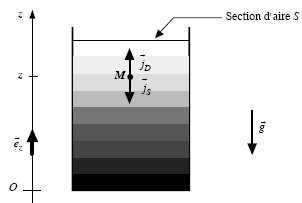Déplacement des particules sous l'action des forces de pesanteur. Ecrire la relation entre les vecteurs v, P, Ff et FA. Pricipe fondamental de la dynamique : P+ Ff + FA =mdv/dt Montrer que la poussée d'Archimède peut s'écrire : FA = r/r0 m g ez. 4/3pR3r0 = m ; FA =  r/r0 m g ez. Proposer une équation différentielle du mouvement d'une macromolécule. Ecrire la relation fondamentale de la dynamique en projection sur l'axe Oz : -mg - f v + r/r0 m g =mdv/dt ; dv/dt +f / m v +g (1-r/r0)=0. (1) En déduire la loi de vitesse en considérant une vitesse initiale nulle. Solution générale de (1) sans second membre : v = A exp(-f / m t) avec A une constante. Solution particulière de (1) : vlim =-mg (1-r/r0 ) / f. Solution générale de (1) : v =A exp(-f / m t) -mg (1-r/r0 ) / f. v(t=0) = 0 ; A = mg (1-r/r0 ) / f. v = -mg (1-r/r0 ) / f (1-exp(-f / m t)). Exprimer la valeur absolue de la vitesse limite de sédimentation. vlim = mg (1-r/r0 ) / f. Soit N*(z) ( particules m-3 ) la densité volumique de particules M à la cote  ( ou altitude ) z. En déduire, en régime de sédimentation établi, les expressions : du nombre dNs ( positif) de particules qui traversent, en decendant, la section droite S du récipient pendant la durée dt. Les particules qui traversent cette section droite pendant la durée dt se trouvaient dans le volume : Sdz = S vlim dt. dNs = N*(z) S vlim dt = N*(z) Smg (1-r/r0 ) / f dt. Du vecteur densité de courant particulaire jS lié à la sédimentation. jS = -1/S dNs /dt = -N*(z) mg (1-r/r0 ) / f  ez. . . Diffusion due à l'hétérogénéité de concentration. La sédimentation ayant entaîné une hétérogénéité de la solution, une diffusion inidimentionnelle et unidirectionnelle ascendante apparaît, soumise à la loi de Fick, de constante de diffusion D ( constante positive ) et de vecteur densité de courant particulaire jD. En tout point du liquide, cette loi s'écrit :  jD = -D grad N*(z) = jD(z) ez. Soit, en régime établi, dND le nombre ( positif) de particules qui traversent, par diffusion et en montant, la section droite S du récipient, pendant la durée élémentaire dt. Rappeller la relation qui lie dND et jD(z). Ces particules se trouvaient dans le volume Sdt : dND = jD(z) S dt. En déduire une relation entre dND et dN*(z)/dz.  dND ez= -D grad N*(z) S dt.  dND = -D  dN*(z)/dz S dt. . Equilibre. Il s'agit maintenant, en tenant compte des deux courants ( de sédimentation et de diffusion ), d'établir la loi N*(z) à l'équilibre. Donner en régime stationnaire et permanent, la relation entre les nombres dNs et dND. A l'équilibre les deux courants se compensent : dNs = dND. En déduire une équation différentielle qui relie N* à la coordonnée de position z.  dND = -D  dN*(z)/dz S dt et dNs = N*(z) S vlim dt. -D  dN*(z)/dz =N*(z)  vlim  ; dN*(z)/dz  +N*(z)  vlim  / D =0. En déduire la loi N*(z), avec N*(z=0) = N*0. N*(z) = A exp(-vlim  / D z) avec A une constante. N*(z=0) =N*0 =A ; N*(z) = N*0 exp(-vlim  / D z). Donner l'allure de la courbe représentative de la fonction N*(z). 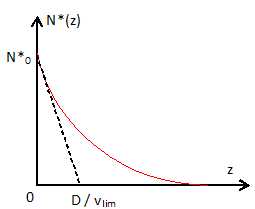Un traitement statistique, selon la théorie de Boltzmann, conduirait à l'expression de la densité volumique particulaire suivante : 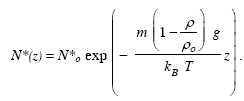avec kB constante de Boltzmann et T température absolue. En déduire une relation entre D, f, kB et T. Par identification vlim / D =m(1-r/r0)g / (kBT) et avec vlim = mg (1-r/r0 ) / f. Par suite : f D =kBT. Or f = 6pRh avec h la viscosité du liquide. Montrer que D peut s'exprimer en fonction de kB, h, T et R. D = kBT /(6pRh). Mesures et résultats. Des mesures optiques à la température T montrent qu'à la cote z1 =4,00 cm, la densité particulaire N* vaut N*(z1) = N*0/3. kB =1,38 10-23 J K-1 ; T = 298 K ; r = 1,00 103 kg m-3 ; r0 = 1,25 103 kg m-3 ; h = 1,00 Pa s. Calculer la masse m et le rayon R des macromolécules. En déduire la valeur de D. (1-r/r0 )gz /(kBT)=(1-1/1,25)*9,81 *0,0400 / (1,38 10-23 *298)=1,9084 10190. N*(z1)=N*0 /3= N*0 exp(-1,9084 1019 m ) ; ln 3=1,9084 1019 m = 1,0986 ; m =5,7568 10-20 ~5,76 10-20 kg. m =4/3 pR3r0  ; R = (3m /(4pr0))1/3 =(3*5,7568 10-20 /(4*3,14*1,25 103)1/3=2,2236 10-8 ~2,22 10-8 m. D =kBT /(6pRh) =1,38 10-23 *298 /(6*3,14*2,2236 10-8 *1,00)=9,81 10-15m2 s-1.

menu