Chocs élastiques.
Concours national Deug
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
On considère 3 particules P1, P2, P3 assimilées à des points matériels de masses respectives m1, m2 et m3 avec m1=m3 = n m2 et n ≥ 1. Ces particules peuvent se déplacer sans frottement suivant la direction Ox.
Initialement, la particule P2 , animée de la vitesse v0 est située entre P1et P3, toutes les deux au repos. La particule P2 vient heurter la particule P1, rebondit, puis heurte la particule P3, rebondit, etc.
On suppose toutes les collisions parfaitement élastiques.
Les vecteurs sont écrits en gras et en bleu.
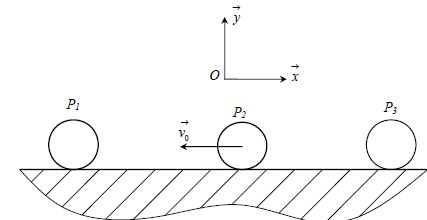
Déterminer les normes v1 et v21 des vitesses, respectivement, des particules P1 et P2 après leur première collision en fonction de n et v0.
Conservation du vecteur quantité de mouvement : m2 v0 = m2 v21 +n m2v1.
v0 = n v1 +v21.
En projection sur Ox : -v0 =-n v1 +v21 (0) soit v02 = n2v12 + v212 -2nv1v21. (1)
Conservation de l'énergie cinétique : ½m2v02 = ½nm2v12 +½m2v212 ;
v02 = nv12 + v212 ; (2)
(1)-(2) donne : 0 =n2v12-2nv1v21-nv12 ; 0 = n v1 -2 v21 - v1 ; v21 = ½ v1 (n-1).
Repport dans (0) : v0 = n v1 - ½ v1 (n-1) ; v1 = 2/(n+1)v0 et v21 =v0 (n-1) / (n+1).
En déduire les normes v22 et v3 des vitesses, respectivement, des particules P2 et P3 après leur première collision en fonction de n et v0.
Conservation du vecteur quantité de mouvement : m2 v21 = m2 v22 +nm2v3.
v21 = n v3 +v22.
En projection sur Ox : v21 =n v3 -v22 (4) soit v212 = n2v32 + v222 -2nv3v22. (5)
Conservation de l'énergie cinétique : ½m2v212 = ½nm2v32 +½m2v222 ;
v212 = nv32 + v222 ; (6)
(5)-(6) donne : 0 =n2v32-2nv3v22-nv32 ; 0 = n v3 -2 v22 - v3 ; v22 = ½ v3 (n-1).
Repport dans (4) : v21 = n v3 - ½ v3 (n-1) ; v3 = 2/(n+1)v21 et v22 =v21 (n-1) / (n+1).
v3 = 2(n-1)/(n+1)2v0 et v22 =v0 (n-1)2 / (n+1)2.
À quelle condition sur n une deuxième collision entre les particules P1 et P2 est-elle possible ?
v22 doit être non nulle soit n différent de 1.
|
| .
. |
|
|
Les particules P1, P2, P3 , toujours alignées, sont maintenant en contact, au repos, dans l’ordre
P1, P3 puis P2. Une autre particule O, supposée ponctuelle, de masse m1 et de vitesse v0 , entre en collision (supposée parfaitement élastique) avec la file, du côté de P1 .
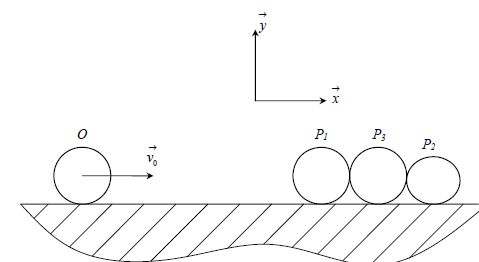
À quelle condition sur n , seule la particule P2 est-elle éjectée après la collision ? Les
particules P1et P3 restent immobiles après la collision.
On note v la vitesse de recul de la particule initiale.
Conservation du vecteur quantité de mouvement : nm2 v0 = nm2 v + m2v2.
nv0 = n v + v2.
En projection sur Ox : n v0 =-n v +v2 (0) soit n2v02 = n2v2 + v22 -2nvv2.
nv02 = nv2 + v22 /n -2vv2.(1)
Conservation de l'énergie cinétique : ½n m2v02 = ½nm2v2 +½m2v22 ;
n v02 = nv2 + v22 ; (2)
(1)-(2) donne : 0=v22 /n -2vv2- v22 ; 0=v2 /n -2v- v2 ; v = ½v2 (1/n-1).
n = 1 et v = 0.
Repport dans (0) : v2 = v0 .
|
.
|