Equilibre d'une
tige.
Concours national Deug
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Soit
une tige homogène de masse m et rigide en forme d'un arc de cercle vue
sous un angle 2a = p
du point O. On note R le rayon du cercle. Cette tige est supportée par
une articulation sans frottement en A et repose en B sans frottement
contre la paroi verticale.
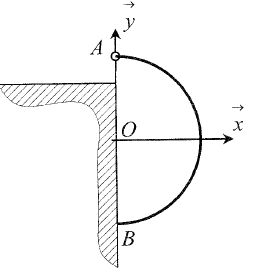
Déterminer les efforts exercés sur la tige en A et B.
Position du centre d'inertie de la tige OG =2R/p.
La tige est soumise à :
- son poids , verticale vers le bas, valeur mg, appliqué en G ;
- action du support en B, perpendiculaire à OB, dirigée vers la droite ;
- action de l'articulation en A.
A l'équilibre, la somme vectorielle des forces est nulle.
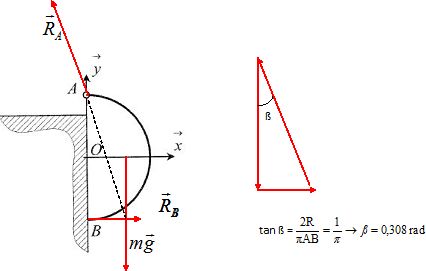
RB = mg tan ß. RA =mg / cos ß.
|
| .
. |
|
|
Maintenant la tige n'est plus supportée qu'au point A.
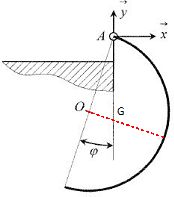
Déterminer la valeur de l'angle j lorsque la tige est en équilibre.
A et le centre de masse G sont sur la même verticale, G en dessous de A.
tan j =OG / OA =2 / p =0,637 ; j =0,567 rad.
|
.
|