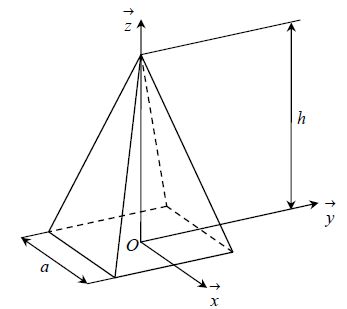
Centre de masse d'une pyramide, d'un demi-cerceau. Concours national Deug En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . On s'intéresse à une pyramide droite de base carrée de côté a et de hauteur h constituée d'un matériau homogène de masse volumique r. Déterminer la masse M de la pyramide en fonction de r, a et h. Volume V = surface de base fois hauteur / 3 = a2h/3. Masse M = rV = r a2h/3. Déterminer la position du centre de masse G de la pyramide. Pa symétrie, G se trouve sur l'axe Oz. On découpe la pyramide en petites tranches d'épaisseur dz parallèlement au plan Oxy. Chaque tranche est un carré de côté. Chaque tranche est un carré de côté b(z) = a ( h-z) / h. La position du centre de masse G est donné par : . . 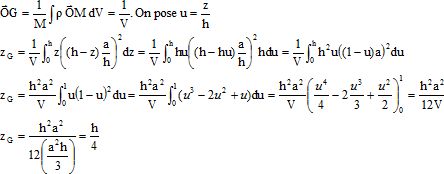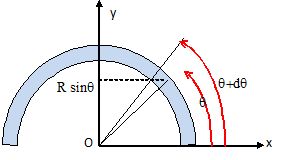Par symétrie, le centre de masse G du demi-cerceau homogène ( de masse volumique r ) est sur l'axe Oy. Soit M la masse du demi-cerceau homogène. On découpe le demi-cerceau en  petits secteurs d'angle dq. Masse d'un secteur : dm = Mdq/p. La position de G vérifie : . 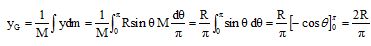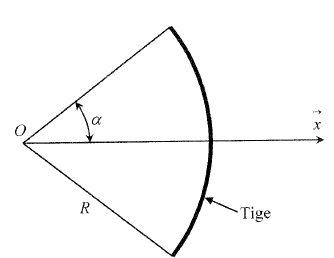Par symétrie, le centre de masse G de la tige homogène ( de masse volumique r ) est sur l'axe Ox. Soit M la masse de la tige homogène. On découpe la tige en  petits secteurs d'angle dq. Masse d'un secteur : dm = Mdq/p. La position de G vérifie : .

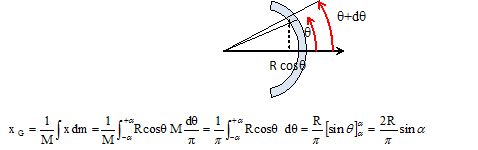
menu